Difference between revisions of "Main Page"
(calc fix (thanks Omega!)) |
|||
| Line 5: | Line 5: | ||
We already have [[:Category:Comics|'''{{#expr:{{PAGESINCAT:Comics}}-3}}''' comic explanations]]!</big> | We already have [[:Category:Comics|'''{{#expr:{{PAGESINCAT:Comics}}-3}}''' comic explanations]]!</big> | ||
| − | (But there are still {{#expr:{{LATESTCOMIC}}-{{PAGESINCAT:Comics}}-3}} to go. Come and [[List of all comics|add yours]]!) | + | (But there are still {{#expr:{{LATESTCOMIC}}-({{PAGESINCAT:Comics}}-3)}} to go. Come and [[List of all comics|add yours]]!) |
</center> | </center> | ||
Revision as of 11:39, 11 August 2012
Welcome to the explain xkcd wiki! We already have 12 comic explanations!
(But there are still 2911 to go. Come and add yours!)
Latest comic
| Scary Triangles |
 Title text: Concealed mostly beneath the surface, sharks are the icebergs of the sea. |
Explanation
| |
This explanation may be incomplete or incorrect: Created by the Bermuda Triangle of the sea - Please change this comment when editing this page. Do NOT delete this tag too soon. |
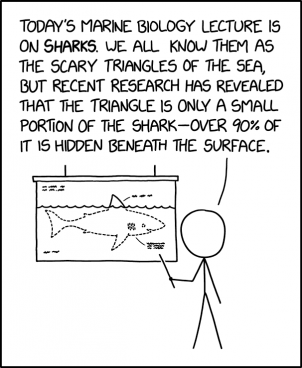
Cueball is giving a marine biology lecture about sharks and seems to have mixed up icebergs with the topic.
In pop culture, sharks will often approach prey or people with only their front dorsal fin visible, which looks like a triangle, above the water. As far as its usual marine prey is concerned, this is inaccurate, as most sharks will attack from below to keep the element of surprise. From the human perspective, we're just more used to (and capable of) seeing the surface of the sea so, most of the time, if we actually know that there is a shark in the area then it's because it is currently swimming close enough to the surface to have its dorsal fin conspicuously sticking into the air - whether or not it is a hunting shark, a dangerous shark or even an actual shark.
In the comic the joke is that Cueball reveals that marine biologists have only recently learned that the triangle is only a small part of a shark. Until this revelation people were only aware of the visible portion, and the fact that death and injury often occurred when they arrive, causing them to be known as 'scary triangles'. Finally the community has learned that more than 90% (i.e. the rest of the shark's body) is hidden beneath the surface. (In most, if not all, cases it would actually be significantly more than 90%.)
The 90% is borrowed from an often cited factoid about icebergs: that 90% of their volume is underwater. (This would be true for clean ice in freshwater, but in reality icebergs are filled with air cavities and float in salt water, so although most of an iceberg is beneath the surface, it is somewhat less than 90%.) Having learned that a similar fact is true of sharks, Cueball has drawn a dotted outline of the shark's body, equivalent to that often depicted in diagrams of icebergs, beneath the scary triangular fin, to show what a shark looks like under the surface. Cueball's enhanced analysis has so far failed to identify some of the even more scary triangles that more often stay below water, and would be experienced proportionately more in actual attack situations, also leaving critical leaky holes in the body.
The title text continues the joke explicitly, saying that sharks are the "icebergs of the sea." However, icebergs are already the icebergs of the sea.[citation needed]
Trivia
This is the second comic in a row to mention sharks (the previous being 2922: Pub Trivia), and the third out of the last five to mention large marine predators in some way (the first being 2919: Sitting in a Tree).
Transcript
- [Cueball points with a stick to a poster hanging behind him to the left. The poster has a diagram of a shark. The dorsal fin is shown above a wavy surface of water. The part of the outline of the shark that are under water are drawn in dashed lines. There are unreadable text in the top and bottom left corner, and two labels with lines that points to its dorsal fin and its gills. Cueball's stick points to the label near the gills]
- Cueball: Today's marine biology lecture is on sharks. We all know them as the scary triangles of the sea, but recent research has revealed that the triangle is only a small portion of the shark - over 90% of it is hidden beneath the surface.
New here?
Feel free to sign up for an account and contribute to the explain xkcd wiki! We need explanations for comics, characters, themes, memes and everything in between. If it is referenced in an xkcd web comic, it should be here.
- If you're new to wikis like this, take a look at these help pages describing how to navigate the wiki, and how to edit pages.
- Discussion about various parts of the wiki is going on at Explain XKCD:Community portal. Share your 2¢!
- List of all comics contains a complete table of all xkcd comics so far and the corresponding explanations. The red links (like this) are missing explanations. Feel free to help out by creating them!
Rules
Don't be a jerk. There are a lot of comics that don't have set in stone explanations, feel free to put multiple interpretations in the wiki page for each comic.
If you want to talk about a specific comic, use its discussion page.
Please only submit material directly related to—and helping everyone better understand—xkcd... and of course only submit material that can legally be posted (and freely edited.) Off-topic or other inappropriate content is subject to removal or modification at admin discretion, and users posting such are at risk of being blocked.
If you need assistance from an admin, feel free to leave a message on their personal discussion page. The list of admins is here.
Logo
Explain xkcd logo courtesy of User:Alek2407.
