Difference between revisions of "153: Cryptography"
(→Explanation: Wikilinks; commas outside quotes) |
|||
| Line 8: | Line 8: | ||
==Explanation== | ==Explanation== | ||
| − | This comic, as the name implies, is relevant to the study of cryptography. | + | This comic, as the name implies, is relevant to the study of {{w|cryptography}}. At the podium, [[Cueball]] is describing a proposed crypto system (a computer program that turns a very large number, called the "{{w|key (cryptography)|key}}", and a message into an encrypted form that can only be read by using the same key), based on the model of a {{w|Feistel cipher}}. Part of any Feistel cipher is the "round function", which determines how the key is applied to the original message; this is applied multiple times with a variety of tricks and techniques to insure the process can eventually be reversed. One common component of round functions is the {{w|S-box}}, a simple table that converts input bytes into output bytes, preferably in a way that doesn't correspond to any mathematical rules. |
Here, the S-box would be implemented by doing the following (with the computer operation actually shown in the diagrams indicated in parentheses): | Here, the S-box would be implemented by doing the following (with the computer operation actually shown in the diagrams indicated in parentheses): | ||
| Line 16: | Line 16: | ||
# Reverse it (run the bits in the opposite order) | # Reverse it (run the bits in the opposite order) | ||
| − | This would be run on each round of the cipher to further scramble the message for the next round. As the caption implies, the steps are based on a line from the Missy Elliott song ''Work It'': "I put my thing down, flip it and reverse it." | + | This would be run on each round of the cipher to further scramble the message for the next round. As the caption implies, the steps are based on a line from the {{w|Missy Elliott}} song ''{{w|Work It (Missy Elliott song)|Work It}}'': "I put my thing down, flip it and reverse it." |
| − | The keyspace for a cryptographic algorithm is the number of possible keys the algorithm can possibly accept. For example, AES-256 has a keyspace of 2<sup>256</sup> (roughly 1.1579209e+77) possible keys, simply because the algorithm specifies that each key is 256 bits wide. The title text is referring to "searching a keyspace, | + | The {{w|Key space (cryptography)|keyspace}} for a cryptographic algorithm is the number of possible keys the algorithm can possibly accept. For example, {{w|Advanced Encryption Standard|AES-256}} has a keyspace of 2<sup>256</sup> (roughly 1.1579209e+77) possible keys, simply because the algorithm specifies that each key is 256 bits wide. The title text is referring to "searching a keyspace", which is to say, simply trying every key until you find one that works. (For reference, a computer would require roughly the energy of a billion billion supernovas to even count to 2<sup>256</sup>, let alone actually try each one.) The precise wording "If you got a big keyspace, let me search it" is, of course, another reference to the same song: "If you got a big **** let me search ya." (The **** in the song is apparently the sound of an elephant, but it is heavily implied from context to be "penis".) |
==Transcript== | ==Transcript== | ||
Revision as of 16:26, 20 June 2013
| Cryptography |
 Title text: If you got a big keyspace, let me search it. |
Explanation
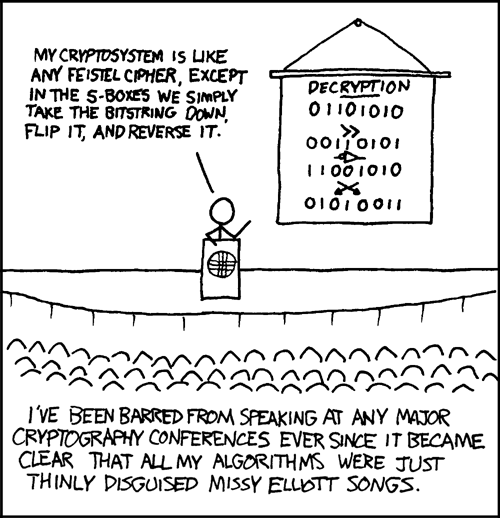
This comic, as the name implies, is relevant to the study of cryptography. At the podium, Cueball is describing a proposed crypto system (a computer program that turns a very large number, called the "key", and a message into an encrypted form that can only be read by using the same key), based on the model of a Feistel cipher. Part of any Feistel cipher is the "round function", which determines how the key is applied to the original message; this is applied multiple times with a variety of tricks and techniques to insure the process can eventually be reversed. One common component of round functions is the S-box, a simple table that converts input bytes into output bytes, preferably in a way that doesn't correspond to any mathematical rules.
Here, the S-box would be implemented by doing the following (with the computer operation actually shown in the diagrams indicated in parentheses):
- Take the bitstring down (roll right by 1)
- Flip it (take its binary NOT)
- Reverse it (run the bits in the opposite order)
This would be run on each round of the cipher to further scramble the message for the next round. As the caption implies, the steps are based on a line from the Missy Elliott song Work It: "I put my thing down, flip it and reverse it."
The keyspace for a cryptographic algorithm is the number of possible keys the algorithm can possibly accept. For example, AES-256 has a keyspace of 2256 (roughly 1.1579209e+77) possible keys, simply because the algorithm specifies that each key is 256 bits wide. The title text is referring to "searching a keyspace", which is to say, simply trying every key until you find one that works. (For reference, a computer would require roughly the energy of a billion billion supernovas to even count to 2256, let alone actually try each one.) The precise wording "If you got a big keyspace, let me search it" is, of course, another reference to the same song: "If you got a big **** let me search ya." (The **** in the song is apparently the sound of an elephant, but it is heavily implied from context to be "penis".)
Transcript
- [Cueball at a podium]
- Cueball: My cryptosystem is like any Feistel cipher, except in the S-Boxes we simply take the bitstring down, flip it, and reverse it.
- I've been barred from speaking at any major cryptography conferences ever since it became clear that all my algorithms were just thinly disguised Missy Elliot songs.
Discussion
I think that executing that S-box twice would get you back where you started. gijobarts (talk) 05:28, 30 July 2013 (UTC)
- Actually that's not true. Regardless of the bit in position 1 to begin with, you will always have a 1 in position 8 in the result. When you shift, you're adding a 0 in position 1 (assuming a 0 shift in), then the inverse is 1, and flipping would put the 1 in position 8. Jarod997 (talk) 14:06, 5 March 2014 (UTC)
- I think it would actually take a few rounds, but yes will eventually get back to the same as the input. Remember that you aren't just doing this operation, you are doing it to one half of the block and then XORing with the other half of the block. But yes I think after a few rounds the XOR's would combine to the identity. (assuming that it wraps, which makes sense to me). Also it is not shown at all how the key would be incorporated into this... so maybe that would help? (or you just add a round key in after doing this operation?) 108.162.218.142 16:32, 18 November 2015 (UTC)
" and so is the author Randall Munroe at PyCon"
- I think that post is a joke.
- It links to 541: TED Talk.
- It says "Registration volunteers have been instructed to refuse admission to Randall Munroe personally, and in fact, to any stick figures who may attempt to register"
- There isn't anything on YouTube or Randall Munroe's Wikipedia page about it.
- Another Python blog says that it was a publicity stunt, citing the organizers' mailing list archives. I didn't bother to sign up for access to the archive.
- Catherine Devlin claims that she banned Randall, so we could try asking her if she's serious.
- Another blog post about it
- gijobarts (talk) 16:48, 2 September 2013 (UTC) (edited 20:29 UTC)
In the same way, a steps to a feistel cipher based algorithm are executed in reverse to obtain the original plain text from a cipher text. is not true. The whole point of a Feistel network is that you execute the same steps in the same order. The only thing that is reversed is the key. You can do almost any amount of mangling of the input, without having to worry about how to reverse it, because the magic of XOR ensures that All Will Be Well when you come to decrypt. There are limits to the kinds of mangling you can do, of course, but the basic principle is that the same function used for encryption is also used for decryption. It's quite startling, really. Horst Feistel - kudos! --BinaryDigit (talk) 15:08, 8 August 2014 (UTC)
- +1 108.162.218.142 16:32, 18 November 2015 (UTC)
"This part needs editing" in what way? It looks fine to me. Clarify, or better yet, edit it in what way you think it needs editing.108.162.219.160 16:08, 29 October 2017 (UTC)
Why is this page marked as an incomplete explanation? 141.101.104.209 16:59, 8 November 2017 (UTC)
The PyCon stuff happened because of 541: TED Talk, and is fully explained there, so is it necessary to have a full PyCon explanation here as well? It seems to me that this comic is not related to PyCon specifically, so would it be enough to just say this is the first comic that mentions getting banned from a conference (and link to Category:Banned from conferences)? If no one objects, I'll do that instead of the current "Inside references and real life shenanigans" section. -- Yfmcpxpj (talk) 13:19, 5 December 2019 (UTC)
- I fully agree. Maybe we can use parts of this text to put it into the category instead? --Lupo (talk) 13:25, 5 December 2019 (UTC)
- Yeah, it's hilarious they would (jokingly) implement the PyCon ban from comic 541 in real life, so I think it's worth a mention in the category page. (But I'm still a noob, so I'm not sure what belongs there.) -- Yfmcpxpj (talk) 14:15, 5 December 2019 (UTC)
- For stuff regarding Categories, usually Kynde has a good feeling. I'll try to reach him on his talk page, to chime in here.--Lupo (talk) 14:21, 5 December 2019 (UTC)
- I completely agree that this section did not belong here, mainly because it was a copy of text already in a section on 541: TED Talk. I have removed it from here adding a link to that section, as it is interesting here to mention given this was the first comic to use this angle, and TED Talk so far is the last. I have also added this text to the category, as TED talk is the one that makes the most out of this ban subject. Maybe the list of banned conferences on TED talk should also add a list of conferences Randall previously have been banned from, mentioning those, if they are not already the same as in that comic? --Kynde (talk) 08:28, 6 December 2019 (UTC)
- Apart from Ted talk they all refer to crypto conferences, which is with one selected one mentioned in Ted Talk, siggraph, which is mentioned, and his math licence, which doesn't refer directly to a conference. So it doesn't need to be mentioned seperately I think. --Lupo (talk) 08:58, 6 December 2019 (UTC)
- I completely agree that this section did not belong here, mainly because it was a copy of text already in a section on 541: TED Talk. I have removed it from here adding a link to that section, as it is interesting here to mention given this was the first comic to use this angle, and TED Talk so far is the last. I have also added this text to the category, as TED talk is the one that makes the most out of this ban subject. Maybe the list of banned conferences on TED talk should also add a list of conferences Randall previously have been banned from, mentioning those, if they are not already the same as in that comic? --Kynde (talk) 08:28, 6 December 2019 (UTC)
- For stuff regarding Categories, usually Kynde has a good feeling. I'll try to reach him on his talk page, to chime in here.--Lupo (talk) 14:21, 5 December 2019 (UTC)
- Yeah, it's hilarious they would (jokingly) implement the PyCon ban from comic 541 in real life, so I think it's worth a mention in the category page. (But I'm still a noob, so I'm not sure what belongs there.) -- Yfmcpxpj (talk) 14:15, 5 December 2019 (UTC)
