Talk:2286: 6-Foot Zone
Ok... 34 feet, in total, but how many hands? (All of which you should wash!) 162.158.34.210 23:34, 27 March 2020 (UTC)
- Love it. Given the extra 1.7 feet for the person, a radius of 20.53 hands. If it were just 6 feet, 18 hands -- brad --108.162.216.122 00:55, 28 March 2020 (UTC)
So Randall is figuring about 1.7 feet diameter for the person. --172.68.174.70 00:40, 28 March 2020 (UTC)
The 190,000 people / mile^2 assumes (I'm guessing) flat ground. Skyscrapers make a difference [citation needed] -- brad --108.162.216.122 00:55, 28 March 2020 (UTC)
Interesting that the population density he gives ignores circle packing. Population should be 174,000. -- coyne -- 162.158.122.156 04:06, 28 March 2020 (UTC)
- Circle packing is unimportant since he's just giving the population of this one circle. He's taking a radius of 6 foot around that person without specifying what he considers to be the radius of the person, but it can be inferred from the numbers:
from area: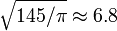 ,
,
from circumference: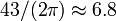 ,
,
from population density: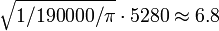 ,
,
so apparently he considers a person to have a radius of 0.8 ft, or about 0.5 m diameter, which seems reasonable. Zmatt (talk) 05:11, 28 March 2020 (UTC) - Note that even if you want to know the population of optimally packed people, your number is still wrong since the circles overlap: your circle is supposed to exclude other people, it doesn't exclude other people's circles. Optimally you'd have a triangular lattice of people with a lattice distance of 7.6 ft (assuming we want 6 ft between people and we consider people to be circles of radius 0.8 ft). This yields a population density of 1 person per
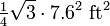 , which is about 1.1 million people per square mile. Zmatt (talk) 05:24, 28 March 2020 (UTC)
, which is about 1.1 million people per square mile. Zmatt (talk) 05:24, 28 March 2020 (UTC)
Much as I love thinking about circle packing density in the plane, I think the above explanation is slightly overthinking the issue. The population density figure appears to be using the idea that one person's zone contains one person; 1 person / (145 ft^2) does indeed equal 192,000 people/square mile. So, he's not saying that 'given these constraints, we can pack people at this maximum density'. He's saying 'given this area, and counting it as a tiny sovereignty, we can calculate its population density to be this'. For this reason, I don't think you should say that the 'population density' figure has an error, only that it is calculated in a different sense than you were thinking about. Dextrous Fred (talk) 18:58, 28 March 2020 (UTC)
Possibly a play on the fact that horses are measured in hands? --orbitalbuzzsaw--
Page 207 of US Forest Service Equestrian Design Guidebook for Trails, Trailheads, and Campgrounds says minimum corral size is 12x12 feet. I didn't find a more likely sounding Forest Service publication. So I assume the handbook in the comic is a fictional publication. Hamjudo (talk) 13:15, 28 March 2020 (UTC)
Always knew cities were bad for humanity. As are airplanes. Need them both to create a pandemic. Seebert (talk) 18:32, 28 March 2020 (UTC)
