Difference between revisions of "2706: Bendy"
(Undo revision 300331 by 172.70.134.49 (talk)) |
m (Fixed new category name) |
||
| (28 intermediate revisions by 23 users not shown) | |||
| Line 10: | Line 10: | ||
==Explanation== | ==Explanation== | ||
| − | {{ | + | Geometry usually represents 2D polygons with simple straight lines. In the comic, the lines are compared to a physical object, and are shown to have the property of bendiness. Randall claims this simplifies geometry as now triangles can have arbitrarily defined side lengths by merely stretching the lines, but it is unclear what benefits this may have over current Euclidean geometry. These lines cannot have Euclidean properties, but other {{w|Non-Euclidean_geometry|non-Euclidean systems have been invented in the past with non-standard properties.}} One such non-Euclidean space can be modelled as the surface of a sphere. If the sphere had a circumference of 20, the triangle with three sides of length 5 would be right angled (at all three vertices). |
| − | + | This comic may be a reference to axis breaks in graphs, which shrink large segments and enhance readability and are denoted by a wiggly line on the axis in question, though this is more frequently done with angular zig-zags than the smoother curves as depicted. | |
| − | + | The title-text talks about "{{w|Squaring the circle}}" (not to be confused with {{w|Tarski's circle-squaring problem|circle-squaring}}), a famous geometry problem based around constructing a square with the same area as a given circle, using a compass and straightedge, which was proven to be impossible (even with more powerful forms of construction, such as marked straightedges or origami) in 1882 as pi is a transcendental number. However, it then goes on to describe a way to literally turn one of these bendy shapes from a circle into a square - namely using clamps. | |
| − | |||
| − | The title-text talks about "{{w|Squaring the circle}}", a famous geometry problem based around constructing a square with the same area as a given circle | ||
==Transcript== | ==Transcript== | ||
| − | + | :[There are two right triangles. The one to the left is a standard right triangle with the right angle denoted by a small square at that corner. The lengths of the sides are denoted around it, but it has been scribbled out with red lines. The triangle to the right has the same general shape as the first one, but with the legs appearing longer but bent with about three wiggles each near the right-angled corner. As with the first triangle, the side lengths are denoted around it, but they are not the same as for the first. Around this triangle is a red line circling about two times around it.] | |
| − | :[There are two right triangles. | + | :Left triangle: 3 4 5 |
| + | :Right triangle: 5 5 5 | ||
:[Caption below the panel:] | :[Caption below the panel:] | ||
| Line 27: | Line 26: | ||
{{comic discussion}} | {{comic discussion}} | ||
| + | [[Category:Comics with color]] | ||
| + | [[Category:Comics with red annotations]] | ||
[[Category:Math]] | [[Category:Math]] | ||
| − | [[Category: | + | [[Category:Geometry]] |
Latest revision as of 07:04, 27 June 2023
| Bendy |
 Title text: Squaring the circle is really easy with some good clamps. |
Explanation[edit]
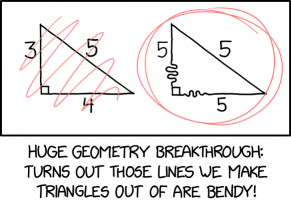
Geometry usually represents 2D polygons with simple straight lines. In the comic, the lines are compared to a physical object, and are shown to have the property of bendiness. Randall claims this simplifies geometry as now triangles can have arbitrarily defined side lengths by merely stretching the lines, but it is unclear what benefits this may have over current Euclidean geometry. These lines cannot have Euclidean properties, but other non-Euclidean systems have been invented in the past with non-standard properties. One such non-Euclidean space can be modelled as the surface of a sphere. If the sphere had a circumference of 20, the triangle with three sides of length 5 would be right angled (at all three vertices).
This comic may be a reference to axis breaks in graphs, which shrink large segments and enhance readability and are denoted by a wiggly line on the axis in question, though this is more frequently done with angular zig-zags than the smoother curves as depicted.
The title-text talks about "Squaring the circle" (not to be confused with circle-squaring), a famous geometry problem based around constructing a square with the same area as a given circle, using a compass and straightedge, which was proven to be impossible (even with more powerful forms of construction, such as marked straightedges or origami) in 1882 as pi is a transcendental number. However, it then goes on to describe a way to literally turn one of these bendy shapes from a circle into a square - namely using clamps.
Transcript[edit]
- [There are two right triangles. The one to the left is a standard right triangle with the right angle denoted by a small square at that corner. The lengths of the sides are denoted around it, but it has been scribbled out with red lines. The triangle to the right has the same general shape as the first one, but with the legs appearing longer but bent with about three wiggles each near the right-angled corner. As with the first triangle, the side lengths are denoted around it, but they are not the same as for the first. Around this triangle is a red line circling about two times around it.]
- Left triangle: 3 4 5
- Right triangle: 5 5 5
- [Caption below the panel:]
- Huge geometry breakthrough: Turns out those lines we make triangles out of are bendy!
Discussion
First time writing a transcript, how'd I do? IJustWantToEditStuff (talk) 07:40, 3 December 2022 (UTC)
- It was a good start. Usually we have colon before each sentence. Also we write all text outside of the square brackets. Even if it is just numbers. When I got here there had been added more. Anytime there are something with color it should be mentioned in the transcript. It is also for those that have poor eyesight. I have now made a version that I think is complete. I'm probably the one that have made most transcripts/completed most at least. But I usually get a lot of help from what other people have made before. Just making them all more alike, following the general rules. So keep up the good work. --Kynde (talk) 15:51, 4 December 2022 (UTC)
Transcript is absolutely fine... Explanation, though, doesn't really explain any more than I already knew, and I still don't "get it". Maybe 'cause I'm dumb after all. 108.162.241.129 15:22, 3 December 2022 (UTC)
I think that this is a joke on non flat geometry, where you can get things like three equal length straight lines (along a sphere perhaps) and have a still have a right triangle, something impossible according to flat geometry A(squared) +B(squared)=C(squared) [a being 1st side B 2nd side C long side [hypotenuse]) i.e. Pythagorean theorum. As seen by this Quora https://www.quora.com/Can-an-equilateral-triangle-be-a-right-triangle-Why-or-why-not
- Perhaps it has to do with Pythagoras and stuff, that at last the “problem” of right triangles with catheti lengths of integers having hypotenuse lengths that are irrational is “solved”. —While False (museum | talk | contributions | logs | rights | printable version | page information | what links there | related changes | Google search | current time: 22:23) 15:27, 3 December 2022 (UTC)
I think this is the comic that made me realize that Randall has never been funny and I've just been checking the comic out of habit. 108.162.221.107 (talk) (please sign your comments with ~~~~)
I think a lot of the time he’s just being silly. It doesn’t have to be super deep. It made me chuckle. Not his best, but he’s made 3 comics a week 2,706 times. They’re not all gonna be S-tier. 172.70.54.52 (talk) (please sign your comments with ~~~~)
I suspect there's also a tie-in with comic 2509 which actually gave the formula for the area (not the volume). I suspect the length of the lines in the right-hand side including the bendy parts, are actually 5. 162.158.106.20 21:06, 3 December 2022 (UTC)
Also see this: (It's not a joke. It may even appear in math tests. Sorry, but I can't upload images) --ColorfulGalaxy (talk) 18:37, 4 December 2022 (UTC)
| |
|\ |-
| \5 ||-7
3| \ 3| |-
| \ | |-
+----- +-----
4 4
- i.e. remember that limits exist? 172.70.134.48 20:34, 4 December 2022 (UTC)Bumpf
Being (semi-?)protected, please could someone make two obvious Transcript corrections (or otherwise render them unnecessary...) ""As with the first the side lenghts lengths are denoted around it, but they are not the same as for the first. Around this triangle are is a red line circling about two times around it." (Also would like to reword "...about two times around it", because "...around two times about it" functionally shows the class of similar meanings I want to avoid. But as I can't change it, I'm not spending effort on working out what I might erroneously consider the better composition. ;) And no disrespect meant to Kynde, for this, as your English is better than my Furrinish, as I've said before. :p ) 172.69.79.158 22:56, 4 December 2022 (UTC)
Why is this protected? It's not a controversial comic anyway. --Theunlucky (talk) 15:57, 5 December 2022 (UTC)
- Due to being subject to excessive vandalism. It was neither due to being controversial, nor due to having a controversial theme, but due to vandalism. 172.68.50.50 18:42, 5 December 2022 (UTC)
Squaring the circle (sphere, whatever) is so easy. Just rearrange the atoms of a sphere into a flat, square sheet. I can definitely do this with my mind and this is not a shitpost at all whatsoever. Psychoticpotato (talk) 18:12, 3 May 2024 (UTC)
ChatGPT explanation[edit]
"This comic is making a humorous comment on the flexibility of the lines used to draw geometric shapes. While in reality, these lines are rigid and cannot be bent, the comic shows that they can be bent and manipulated to create different shapes. The red lines scribbling out the first triangle and the wavy lines of the second triangle emphasize this point."
(I omitted the paraphrasing of the transcript.) Obviously this is a very surface-level take, but satisfactory for a three sentence paragraph. 162.158.166.172 17:30, 7 December 2022 (UTC)
