Difference between revisions of "2610: Assigning Numbers"
(→Explanation) |
(Deleted the line about biology and human behavior in the explanation of the title text, because the title text specifically mentions branches of mathematics) |
||
| (18 intermediate revisions by 11 users not shown) | |||
| Line 8: | Line 8: | ||
==Explanation== | ==Explanation== | ||
| − | |||
'''This explanation is by mathematical necessity either incomplete or incorrect.''' | '''This explanation is by mathematical necessity either incomplete or incorrect.''' | ||
| Line 23: | Line 22: | ||
This allowed Gödel to make the statement "This statement cannot be proven based on the axioms provided" in a mathematically rigorous way. A simple proof by contradiction shows that the statement cannot be false, and therefore (in most logical systems) must be true. The proof goes as follows: 1. Assume that "This statement cannot be proven from the axioms" (Call this statement G) is false.<ref>Call this assumption A.</ref> 2. Therefore G can be proven from the axioms.<ref>Because the negation of the negation is an affirmation. Based only on A.</ref> 3. The axioms exist.<ref>Call this assumption B</ref> 4. Therefore, G is true.<ref>via {{w|Modus ponens}} applied to 2 and 3, based on A and B</ref> 5. Therefore, G and also not G.<ref>via {{w|Conjunction introduction}} applied to 1 and 4, based on A and B</ref> 6. This is a contradiction, and therefore A (that is, 'not G') or B (ZFC) must be wrong. We are not willing to sacrifice assumption B, so we must conclude that A is false, given B.<ref>{{w|Reductio ad absurdum}} applied to 1,3, and 5</ref> 7. Therefore, G. | This allowed Gödel to make the statement "This statement cannot be proven based on the axioms provided" in a mathematically rigorous way. A simple proof by contradiction shows that the statement cannot be false, and therefore (in most logical systems) must be true. The proof goes as follows: 1. Assume that "This statement cannot be proven from the axioms" (Call this statement G) is false.<ref>Call this assumption A.</ref> 2. Therefore G can be proven from the axioms.<ref>Because the negation of the negation is an affirmation. Based only on A.</ref> 3. The axioms exist.<ref>Call this assumption B</ref> 4. Therefore, G is true.<ref>via {{w|Modus ponens}} applied to 2 and 3, based on A and B</ref> 5. Therefore, G and also not G.<ref>via {{w|Conjunction introduction}} applied to 1 and 4, based on A and B</ref> 6. This is a contradiction, and therefore A (that is, 'not G') or B (ZFC) must be wrong. We are not willing to sacrifice assumption B, so we must conclude that A is false, given B.<ref>{{w|Reductio ad absurdum}} applied to 1,3, and 5</ref> 7. Therefore, G. | ||
| + | |||
| + | ===Explanatory footnotes for the above=== | ||
| + | <references /> | ||
Notice that the truth of Gödel's statement does not depend on any particular set of axioms, and adding axioms (such as "Gödel's particular statement is true") only opens up new iterations of the statement which cannot be proven based on the expanded set of axioms (A statement such as "All statements of a similar nature to Gödel's particular statement" is not precise enough to serve as an axiom.). As such, with a little more legwork, it can be proven that any logical system robust enough to accommodate arithmetic must necessarily contain facts that are true within the system but cannot be proven or disproven within the system. The importance of this result cannot be understated, as it upended the entire philosophy of mathematics. {{w|David Hilbert}}'s famous proclamation "We must know, we will know" is simply incorrect. ... Either that, or (ironically) Gödel used an "inconsistent" or "incomplete" system to produce his result. | Notice that the truth of Gödel's statement does not depend on any particular set of axioms, and adding axioms (such as "Gödel's particular statement is true") only opens up new iterations of the statement which cannot be proven based on the expanded set of axioms (A statement such as "All statements of a similar nature to Gödel's particular statement" is not precise enough to serve as an axiom.). As such, with a little more legwork, it can be proven that any logical system robust enough to accommodate arithmetic must necessarily contain facts that are true within the system but cannot be proven or disproven within the system. The importance of this result cannot be understated, as it upended the entire philosophy of mathematics. {{w|David Hilbert}}'s famous proclamation "We must know, we will know" is simply incorrect. ... Either that, or (ironically) Gödel used an "inconsistent" or "incomplete" system to produce his result. | ||
| Line 29: | Line 31: | ||
:1) Gödel is long dead, and dead people can't write articles;{{Dubious}}<sup> - see [[599: Apocalypse]]</sup> | :1) Gödel is long dead, and dead people can't write articles;{{Dubious}}<sup> - see [[599: Apocalypse]]</sup> | ||
:2) Gödel numbers grow very large very quickly, and depend heavily on the specific values assigned to each logical operator. Therefore the results could be manipulated simply by changing the numbering order of each operator; | :2) Gödel numbers grow very large very quickly, and depend heavily on the specific values assigned to each logical operator. Therefore the results could be manipulated simply by changing the numbering order of each operator; | ||
| − | :3) It may be very hard to gather all theorems in a field, or even a representative sample | + | :3) It may be very hard to gather all theorems in a field, or even a representative sample |
| − | |||
If anyone were to attempt this form of analysis, it would be an example of the bad data science described in the caption. | If anyone were to attempt this form of analysis, it would be an example of the bad data science described in the caption. | ||
Latest revision as of 02:29, 10 March 2024
| Assigning Numbers |
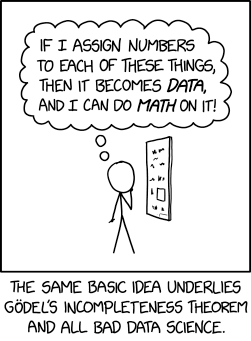 Title text: Gödel should do an article on which branches of math have the lowest average theorem number. |
Explanation[edit]
This explanation is by mathematical necessity either incomplete or incorrect.
Cueball is falling into a common trap, because a little knowledge is a dangerous thing. Faced with some sort of information, of an unknown kind but seemingly not intrinsically mathematical in nature, he has decided that one possible way to proceed is to somehow translate everything into values which can be combined and compared numerically.
This is a very common thing to do, in fields as diverse as computational linguistics or sports analytics, and can be a powerful tool for understanding and learning new things about a subject as Data science tries to extract knowledge and insights from potentially noisy and disordered facts. But it is also used to implement bad science by using incorrect or misguided ideas about how to represent the source material. While it's possible to casually assign numeric values to random pieces of data, these numbers are generally not meaningful enough to compute with and draw any useful inferences from. It is generally possible to perform statistical analysis only on actual measurements, not on what may effectively be arbitrarily-assigned values.
Machine learning algorithms, which are commonly used by data scientists, typically require all their inputs to be numerical. However, most datasets contains categorical features (e.g. the description of a piece of furniture: chair, table, ...). Data scientists therefore use encoding techniques to convert these categorical features to a numerical form so they can be used as inputs to a machine learning model. For instance, label encoding consists of arbitrarily assigning an integer to a category (chair=0, table=1, ...) which may appear meaningless to most observers. In various cases, they may be right.
So, as well as being the mechanism that underlies one of the most profound theorems of 20th century mathematics, it can be mis-used for all kinds of bad or misguided science. From Cueball's attitude, it is far from clear that his attempt will reliably translate his project into a numerical system, nor that his attempt to "do math on it!" will be any more competent.
One of the major characters who looked at the concept is Kurt Gödel. He introduced the idea of Gödel numbering with his landmark incompleteness theorems. In it a unique natural number is assigned to each axiom, statement, and proof, which might otherwise be difficult to accurately process in any other kind of approach. Instead, it is now possible to create metamathematical statements in the language of mathematics.
This allowed Gödel to make the statement "This statement cannot be proven based on the axioms provided" in a mathematically rigorous way. A simple proof by contradiction shows that the statement cannot be false, and therefore (in most logical systems) must be true. The proof goes as follows: 1. Assume that "This statement cannot be proven from the axioms" (Call this statement G) is false.[1] 2. Therefore G can be proven from the axioms.[2] 3. The axioms exist.[3] 4. Therefore, G is true.[4] 5. Therefore, G and also not G.[5] 6. This is a contradiction, and therefore A (that is, 'not G') or B (ZFC) must be wrong. We are not willing to sacrifice assumption B, so we must conclude that A is false, given B.[6] 7. Therefore, G.
Explanatory footnotes for the above[edit]
- ↑ Call this assumption A.
- ↑ Because the negation of the negation is an affirmation. Based only on A.
- ↑ Call this assumption B
- ↑ via Modus ponens applied to 2 and 3, based on A and B
- ↑ via Conjunction introduction applied to 1 and 4, based on A and B
- ↑ Reductio ad absurdum applied to 1,3, and 5
Notice that the truth of Gödel's statement does not depend on any particular set of axioms, and adding axioms (such as "Gödel's particular statement is true") only opens up new iterations of the statement which cannot be proven based on the expanded set of axioms (A statement such as "All statements of a similar nature to Gödel's particular statement" is not precise enough to serve as an axiom.). As such, with a little more legwork, it can be proven that any logical system robust enough to accommodate arithmetic must necessarily contain facts that are true within the system but cannot be proven or disproven within the system. The importance of this result cannot be understated, as it upended the entire philosophy of mathematics. David Hilbert's famous proclamation "We must know, we will know" is simply incorrect. ... Either that, or (ironically) Gödel used an "inconsistent" or "incomplete" system to produce his result.
The title text suggests that Gödel should perform such an analysis on different branches of mathematics, by calculating the average of all the fields' theorems' Gödel numbers. This is nonsensical for a number of reasons:
- 1) Gödel is long dead, and dead people can't write articles;[dubious] - see 599: Apocalypse
- 2) Gödel numbers grow very large very quickly, and depend heavily on the specific values assigned to each logical operator. Therefore the results could be manipulated simply by changing the numbering order of each operator;
- 3) It may be very hard to gather all theorems in a field, or even a representative sample
If anyone were to attempt this form of analysis, it would be an example of the bad data science described in the caption.
Transcript[edit]
- [Cueball holds a hand up to his chin while he ponders the contents of what may be a whiteboard. There are five general lines of unreadable scribbling on the board, and between the two bottom lines, there is a square frame to the right with another scribble to the left. Cueball's thoughts are shown above him in a large thought bubble.]
- Cueball's thinking: If I assign numbers to each of these things, then it becomes data, and I can do math on it!
- [Caption beneath the panel:]
- The same basic idea underlies Gödel's Incompleteness Theorem and all bad data science.
Discussion
Does this imply that Gödel's Incompleteness Theorem isn't correct? And that it's method is bunk? Please help! -Seer 162.158.107.230 02:08, 23 April 2022 (UTC) I believe the intention is that the theorem is not part of the set of bad data science, just that they share this one feature.
Isn't the Gödel number for a theorem calculated by multiplying the numbers of the components together, so complicated theorems would have larger numbers? If so, the current explanation that this isn't a good way to judge fields is wrong. I'm not too sure though. MrCandela (talk) 05:52, 23 April 2022 (UTC)
- I do not believe that the title suggests renumbering theorems with Gödel numbers, but averaging the existing theorem numbers. Or otherwise, MrCandela's suggestion would be the way to go: Complicated Theorems have larger numbers. Sebastian --172.68.110.133 08:10, 23 April 2022 (UTC)
- Yeah a quick look at some magazines like this one and I think Randall has a point MrCandela (talk) 09:48, 23 April 2022 (UTC)
I wish I'd started the explanation off when I first saw it (somone posted the first Transcript whilst I was pondering, so I left off). I think there's some serious re-editing to be done, but basically it points to someone (Cueball, a dabbling armchair mathematician faced with some not directly mathematically-based problem) thinking that 'all' it takes is to encode the whatever-it-is, arbitrarily, and then with a few easy equations something useful cannbe derived. When, in reality, even if this is possible (ignoring the "takes the age of the universe to permute things to find the right answer" sort of sticking-block) it depends upon a good numerical encoding (enough attention to detail, but not too much, and in the right sort of way) and possibly quite a lot of data-demunging and filtration (again, just the right amount and in the correct manner) to pop out the "answer" being looked for. For some things, this can be easy, though there are always statistical pitfalls/etc. For others ("life, the universe and everything", say) the task is far more complex and the result ("42"?) might not seem to be a very useful result for various reasons. And, on top this, there's Gödel. But that's an additional punchline, not the whole scope of the original joke. ...Anyway, this long comment is why I held back from writing the original Explanation, but I might yet wrangle my thoughts into what's since been put there. While trying not to tread upon too many toes and alternate explanations. Which is the hardest bit, I think... 172.70.86.64 15:48, 23 April 2022 (UTC)
Just a comment about the technicalities of Gödel's First Incompleteness Theorem: The 'third' possibility presented here misunderstands the term 'true but unprovable'. When mathematicians say 'true but unprovable' in the context of Gödel's Incompleteness Theorems, what they mean is 'true in the standard model but unprovable in the formal system'. The Gödel sentence is certainly true for the standard natural numbers, by contradiction: assume that the Gödel sentence is false for the standard naturals, which means that there exists a standard natural number which is the Gödel number for the proof of the Gödel sentence. Then we could decode the Gödel number into a proof (of the formal system) proving the Gödel sentence true; a contradiction. (Note that the preceding proof by contradiction can be formalised in ZFC, but not in the formal system under study.) The reason why the Gödel sentence is unprovable in the formal system is because, from the point of view of the formal system, there might be a non-standard natural number which is the Gödel number for the proof of the Gödel sentence (and non-standard numbers cannot be decoded into a proof); or there might not be. --Underbase (talk) 04:56, 24 April 2022 (UTC)
- Regarding this, I know that the policy on this site is to include every possible interpretation, but the page mentioned is an html page (and not a pdf) that was not peer reviewed (thus not recognized by the community), and as mentioned by the user above it fails understand the concepts it is talking about. I do not think this site should be spreading this kind of idea. I believe Randall Monroe himself would be against this.
- I also believe the current explanation is both incorrect about explaining the seeming paradox of the Gödel conjecture, & therefore somewhat incorrect about this joke. It is surely the transition from abstract to quantized - the act of applying limited formal numbering to potentially unbounded or otherwise non-standard terms - which incurs incompleteness? Within the constraints of a formal system of standard natural numbers, true≠provable, & therein lies the internal (but not total) contradiction. That's the contradiction, right? & the joke is that numbering theorems by their complexity, is not generally a productive approach for 'doing math' on them, in any sense but an abstract analytical one?
- ProphetZarquon (talk) 17:54, 24 April 2022 (UTC)
- I do not believe the Title Text calls for "calculating the average of all the fields' theorems' Gödel numbers". It asks for 'the lowest average theorem number'. The average of all, is not the average of each. The Title Text wants the average of each of the fields' theorems' Gödel numbers.
- ProphetZarquon (talk) 17:54, 24 April 2022 (UTC)
Today's Saturday Morning Breakfast Cereal is slightly related.
Paradoxicality argument[edit]
I think that revision 231000 should be removed. My explanation of what's wrong with the linked site is as follows:
Up until the section "Gödel's String", nothing is incorrect. Furthermore, the first wrong line is numbered (49), and says that Gödel's statement is equivalent to "This statement is not a theorem (of any formal system)." This is where he goes wrong, for writing down a formula for "n proves m" requires inclusion of the formal system in which this proof happens. As such, the correct translation of Gödel's statement is "This statement is not a theorem of [system]", which it indeed is not. Then he says that "We have decided that Gödel's string cannot be a theorem and neither can its negation" (true, after Rosser's trick) and therefore that this gives us "~<G∨~G>" (which is false). He has commited the sin of confusing truth and provability here.
His discussion of the Epimenides string ("This statement is not true") is accurate, except for the claim that the truth predicate is "as valid an extension to [PA] as [the provability and quining] extensions were". This is false. The provability and quining predicates can be constructed in PA and thus are not "extensions" so much as "shorthand"; this was Gödel's contribution: to see that PA can talk about provability of statements in any fixed formal system. The truth predicate is not definable in PA, as he quite ably proves (suppose it was definable, then you could write down the Epimenides sentence in PA, and thereby prove false).
The section "Gödel's Error" is just plain silly.172.70.114.147 19:28, 24 April 2022 (UTC)
What if we just change it to say something along the lines of "Certain logical systems allow values to be 'not false' without being necessarily 'true'; Godel's theorem is based on an axiomatic assumption that every statement is either true or false."?108.162.221.163 06:06, 25 April 2022 (UTC)
Is it just me, or is the given argument gibberish? Replacing the terms with more graspable ones, it seems to be saying: "1. Assume that bananas can be grown from banana-trees (why is this a reasonable assumption? Is it also a reasonable assumption to make about pear trees?). 2. Banana-trees exist. 3. Therefore, the statement that bananas cannot be grown from the trees is true (HOW is this a reasonable conclusion to leap to from the preceding points? By what bizarre leap of elided logic?). 4. This is a contradiction, therefore our initial assumption must be wrong (No, clearly the conclusion in 3 is wrong). Therefore, the statement is true (which statement are you even talking about here?)." Any chance someone could clarify that passage by including the missing steps in the logic? --172.69.70.159 19:02, 25 April 2022 (UTC)
- It's not missing any steps. The argument really is that simple. Maybe I didn't write it clearly enough... Anyway to address your specific points, I would first recommend you read Reductio ad absurdum, but if you don't have time (Because let's be real, nobody has enough time for reading Wikipedia articles), I'll break it down. 1. Assume the opposite of the statement (This is not a reasonable assumption almost by definition; the whole point is to disprove it, after all) using the Law of Assumption, which states that we can assume absolutely anything we want in a logical proof, so long as we keep track of what's been derived from it. 2 Assume anything else relevant 3. Follow the assumptions through to their conclusions, and find that the valid reasoning has led to an unsound result, such as a statement directly contradicting the assumption in 1. 4. One of the assumptions must be wrong in order to maintain consistency. Choose the assumption which was made for the purpose of disproving it to be the one we deem untrue, which means its opposite is true. Unfortunately these sorts of arguments don't really lend themselves to analogies with 'more graspable' statements.108.162.221.193 02:30, 26 April 2022 (UTC)
Hello,
1) Why couldn't Gödel's string be paradoxical? It is certainly A) self-referencing and B) Self-negating. Even "This Statement is True" causes trouble.
2) Where did Gödel even consider paradox to be a possibility? If he didn't, his argument is "incomplete" (just like its conclusion implies it might very well be anyway).
3) Has anyone here bothered to prove that his string is not actually paradoxical?
- Don Stoner (nobody in particular -- just a senile wimpy old nerd)
Hi again, Here's a fun one: "This statement is paradoxical" 1) It certainly is paradoxical (provably so) 2) It even says it's paradoxical (echoing Gödel) 3) Therefore, it must be "true" (echoing Gödel) 4) But (this time) this means it's simply "false" 5) Etc. - Don (nobody in particular)
- 1) I'm not sure what you mean by "paradoxical". If you mean something like "true and false" or "neither true nor false", that fails classical logic. Gödel (with a bit of help from Rosser) proved that we can write down a sentence G of Peano arithmetic, then prove (in PA) that G is equivalent to "no integer encodes a proof in PA of G unless a smaller one encodes a proof in PA of not G". He then pointed out that if G was provable in PA, there was also a proof of not G (basically, work out what integer encodes that proof of G, then for each smaller integer, try to decode it into a proof of not G; if you succeed, you have a proof of not G; if you fail for all, you have proved by exhaustion that your integer encodes a proof of G and no smaller integer encodes a proof of not G; all this is a proof of not G). Thus, if PA is consistent, there is no proof in PA of G. Now assume there is a proof in PA of not G. Encode this proof into an integer N. We shall now prove either G or "every integer less than N does not encode a proof in PA of G". We thus work through every integer less than N, checking to see if it encodes a proof in PA of G. If it does we have proved G; if no integers less than N encode a proof of G then we have proved "for all n < N, n does not encode a proof in PA of G". In the latter case, we have proved that every integer encoding a proof in PA of G is greater than N, which is an integer encoding a proof in PA of not G; this implies G! As such, we started with a proof in PA of not G (NOTE: THIS IS DIFFERENT FROM MERELY ASSUMING not G), and produced a proof in PA of G. So if PA is consistent, there is no proof in PA of not G either. Hence PA is either inconsistent (as if PA proves either G or not G, it proves the other and hence false) or incomplete (proving neither).
- 2) He proved that either PA proves false, or there is a statement such that PA proves neither the statement nor its negation. The first includes paradoxicality. (His second incompleteness theorem was essentially: "By the argument above, PA proves that if PA is consistent then G has no proof in PA, which easily implies that PA proves "If PA is consistent, then G". Now suppose PA proves that PA is consistent. Then by modus ponens, PA proves G, and therefore PA is inconsistent. So if PA proves that PA is consistent, then PA is inconsistent.") (It is possible for a consistent system to prove its own inconsistency.)
- 3) Most mathematicians assume that ZFC is consistent, even augmented by some pretty strong large cardinal hypotheses. 172.70.35.72 17:11, 27 April 2022 (UTC)
- The short answer to your questions is that Godel's method was rigorous. Godel numbering is much more precise than natural language ever could be. The longer answer is that there's a reason Godel's theorem is considered a work of genius; though the overall concept is fairly easy to grasp intuitively, making it into an actual theorem takes a lot of work and cleverness. There are multiple long Wikipedia pages about it just outlining the generals. The proof itself is rock solid, but far beyond the scope of this page. And the pithy answer is "Do you really think you're the first person to think of that? Mathematicians spent decades analyzing the theorems with uncharitable eyes."108.162.221.119 04:12, 27 April 2022 (UTC)
- I am certain I am not the only person to notice his error because I have been contacted by others who noticed it independently. (None of us were sufficiently arrogant to presume we were first.) Further, we have all spent a great deal more time investigating this than you presume. Gödel's numbering was indeed rigorous and precise, but in spite of his genius, he simply failed to consider the possibility of paradox (incompleteness). If I am wrong about this, it would be would be a simple matter to show me where he addressed this. - Don Stoner (n.i.p.)
I'm going to remove the section stating that Godel's theorem is self-negating (it's not) and that his methodology was incomplete. And before anyone re-adds it, I simply ask that you please please PLEASE actually read up on the subject (and I don't mean from random html pages). Mathematicians have been actively trying to find a flaw in Godel's proof since before it was published; I promise you that whatever clever paradoxicality argument you've come up with has already been considered and eliminated by the professionals.108.162.221.81 21:59, 27 April 2022 (UTC)
- Your parting shot kind of reminds me of Junior high school. Specifically, I was one nerd being confronted by a few dozen "normal" kids. I was outnumbered, but there was really only room for one kid to get in my face at a time. As I told each of those kids (one at a time), "Your buddies aren't here right now. It's just you and me." So, unless you can talk one of those "professionals" (who actually understands Gödel's proof) into joining us here, you need to explain to me where Gödel addressed the possibility of paradox (he didn't). His methodology was incomplete. You also need to explain to me why you assert that "This statement cannot..." is not self-negating (it is). Further, since "the policy on this site is to include every possible interpretation" you also need to explain to me why you have taken it upon yourself to override Randal's authority. - Don Stoner (n.i.p.)
- I can't even be bothered to work out who is saying what. Don, if you're interested in site policy, use the proper ~~~~ signature (get an account in your name, if you want to be named), and possibly chill out a bit too. If someone is arguing (can't be bothered to check the edit history/diffs) then they need to use a .sig too. And colon-indents per level of reply is useful. But don't mind me, it looks like you're having fun either on your own or as a pair (or more). Just sayin'... 162.158.159.71 17:54, 27 April 2022 (UTC)
- Thanks! (I'm a retired robotics-embedded-system programmer, but I'm not much of an end used. I need help to use my cellphone.) - Don --172.69.34.10 19:55, 27 April 2022 (UTC)
- Oops, sorry, I didn't properly sign my comment. Normally I'm pretty diligent about it, so looking back at this I didn't even recognize my own writing for a few seconds (insert laughing emoji). I'll go back and add a signature now. The time stamp will be wrong, but I don't know a way around that.108.162.221.81 21:59, 27 April 2022 (UTC)
- I can't even be bothered to work out who is saying what. Don, if you're interested in site policy, use the proper ~~~~ signature (get an account in your name, if you want to be named), and possibly chill out a bit too. If someone is arguing (can't be bothered to check the edit history/diffs) then they need to use a .sig too. And colon-indents per level of reply is useful. But don't mind me, it looks like you're having fun either on your own or as a pair (or more). Just sayin'... 162.158.159.71 17:54, 27 April 2022 (UTC)
- To clarify, I removed the section because it stated as fact that the incompleteness theorem is wrong. If you don't like the theorem, that's fine, but the consensus view is that the proof is sound. I did add a sentence to the effect of 'it's always possible we're wrong about things' to hopefully reflect the point of view that had been stated with unwarranted confidence. If that's not an acceptable compromise to people, you're welcome to counter propose.108.162.221.81 22:00, 27 April 2022 (UTC)
- If my memory serves correctly, what you removed was:
- "Either that, or Gödel used an "inconsistent" or "incomplete" system to produce his result. Any "complete and consistent" system would recognize a self-referencing and self-negating statement to be a form of the 'liar's paradox' ('This statement is false')." Gödel did not examine that as a possibility (incomplete methodology).
- 1) Gödel himself demonstrated that his (or any) formal system was either "inconsistent" or "incomplete." This much is both ironical and obviously true.
- 2) It is observable fact that Gödel did not consider paradox as a possibility. This makes his theorem "incomplete." This is observable fact, not a false claim.
- Censoring my opinion is not a legitimate "compromise." I recommend that you attempt to refute (or at least counter) my opinion instead. - Don --172.70.207.8 22:55, 27 April 2022 (UTC)
- I tried a cropped (and less controversial) version of my original statement, to see what you thought about it.--162.158.78.229 02:20, 28 April 2022 (UTC)
- I'm not entirely sure what you mean by "paradox"; to my knowledge, that word doesn't have a formal mathematical definition. I assume you mean a non-true non-false statement? (feel free to correct me) In which case, Gödel did not consider this because he was working within classical logic, wherein statements can either be "true" or "false" and there is no third value. The reason he chose classical logic is because mathematics is currently performed using classical logic. And although most proofs of "the Gödel sentence is true" are a bit wishy-woshy, you can actually formalise a proof within ZFC set theory (a theory based on classical logic) that the Gödel sentence is true for the standard natural numbers (see my comment above). Of course, you could reject ZFC (and base mathematics on something like paraconsistent logic) but you'll probably have a hard time convincing mathematicians. Regardless, was more concerned with the incompleteness of the system than with the truth of the Gödel sentence, and doesn't mention truth at all in Theorem VI (the First Incompleteness Theorem) of his original paper.--Underbase (talk) 10:43, 28 April 2022 (UTC)
- I won't argue with that. (I'll also back off to "non-true non-false," since I'm unsure how to understand other definitions.). "Incompleteness" (rather than "inconsistency") is still the missing piece. One claim in the above explanation: "David Hilbert's famous proclamation "We must know, we will know" is simply incorrect," Ignores this qualification -- making it a misapplication of what Gödel actually proved. Maybe we can eventually know truth -- but the limited tools constituting Gödel's proof were simply not up to that task.--172.69.33.83 20:04, 28 April 2022 (UTC) -edited --172.70.214.81 21:26, 28 April 2022 (UTC)
- The point of the theorem is that any system containing arithmetic is EITHER incomplete or inconsistent. If it is incomplete, then the point stands that there are things we can't know with it. If it is inconsistent, that means it can prove paradoxes (which is what you seem to be saying was overlooked). However, if you can prove a paradox, then you can then use that proven paradox to prove anything at all you want to and its opposite at the same time regardless of anything. Accepting any one paradox as true means that you can then prove one equals five for example. The thing about that is, if that's the system you're trying to base things on, then rather than some things you don't know, you don't know anything meaningful at all. You basically are saying "he overlooked that the possibility that whole system all mathematicians use is incoherent nonsense, so all proofs are flawed including this one." Also, the statement "this statement is a paradox" you mentioned, isn't a paradox, it's simply a necessarily and obviously false statement.--172.70.126.221 09:31, 16 May 2022 (UTC)
- I won't argue with that. (I'll also back off to "non-true non-false," since I'm unsure how to understand other definitions.). "Incompleteness" (rather than "inconsistency") is still the missing piece. One claim in the above explanation: "David Hilbert's famous proclamation "We must know, we will know" is simply incorrect," Ignores this qualification -- making it a misapplication of what Gödel actually proved. Maybe we can eventually know truth -- but the limited tools constituting Gödel's proof were simply not up to that task.--172.69.33.83 20:04, 28 April 2022 (UTC) -edited --172.70.214.81 21:26, 28 April 2022 (UTC)
- I'm not entirely sure what you mean by "paradox"; to my knowledge, that word doesn't have a formal mathematical definition. I assume you mean a non-true non-false statement? (feel free to correct me) In which case, Gödel did not consider this because he was working within classical logic, wherein statements can either be "true" or "false" and there is no third value. The reason he chose classical logic is because mathematics is currently performed using classical logic. And although most proofs of "the Gödel sentence is true" are a bit wishy-woshy, you can actually formalise a proof within ZFC set theory (a theory based on classical logic) that the Gödel sentence is true for the standard natural numbers (see my comment above). Of course, you could reject ZFC (and base mathematics on something like paraconsistent logic) but you'll probably have a hard time convincing mathematicians. Regardless, was more concerned with the incompleteness of the system than with the truth of the Gödel sentence, and doesn't mention truth at all in Theorem VI (the First Incompleteness Theorem) of his original paper.--Underbase (talk) 10:43, 28 April 2022 (UTC)
- If my memory serves correctly, what you removed was:
I, for one, am very pleased with the current compromise. The use of ellipsis and the inclusion of "(ironically)" has totally sold me on it. Also, if anyone knows how to make those notes where you have the little number you can click on to see the full explanation, I think the proof by contradiction part could benefit from having the parenthetical statements moved to notes. I'm going to look up how to do it, and I'll try, but if it all goes horribly wrong...108.162.221.101 20:27, 4 May 2022 (UTC)
