Difference between revisions of "1213: Combination Vision Test"
(→Transcript) |
m (rv) |
||
| (39 intermediate revisions by 18 users not shown) | |||
| Line 8: | Line 8: | ||
==Explanation== | ==Explanation== | ||
| + | {{w|Synesthesia}} is a condition in which perception in one sensory or cognitive pathway leads to automatic, involuntary experiences in a second sensory or cognitive pathway. Common examples are experiencing colors when seeing numbers or words ({{w|Grapheme-color synesthesia}}), hearing tones or music while reading words or text, seeing sequences of numbers or month names in a distinct and fixed shape ({{w|Number form}}), etc. In [[1608: Hoverboard]] [[Megan]] stands at [http://www.explainxkcd.com/wiki/images/9/9d/1608_1090x1088y_Megan_want_synesthesia_at_the_rear_end_at_bottom_of_the_hull.png the end of the Star Destroyer] and wishes she had synesthesia so bad she can taste it... | ||
| − | + | {{w|Color-blindness}} is one of a number of conditions in which a person cannot distinguish certain pairs of colors that other people without color-blindness might find easy to distinguish. There are many different forms of color-blindness; the most common is an inability to separate the colors red and green. | |
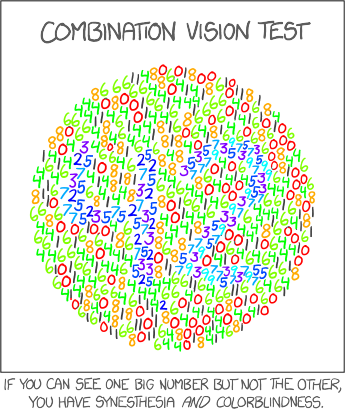
| − | + | There are two numbers embedded in the big circle of numbers, in a similar way to a common {{w|color perception test}}. But this test can not work for colors because it is just a black-and-white picture. Nobody can see it. However, the joke lies in the fact that those with one common form of synesthesia see colors associated with numbers. Randall implies that a synesthete will see colors connected to each number, and thus a color perception test will work after all - thus distinguishing synesthetes with color-blindness from those with normal color perception. | |
| − | the number 2 is | + | The comic playfully suggests that if you have synesthesia as well as {{w|colorblindness}}, then some of the colors might appear identical and so one number would not be visible, only leaving the other number. |
| + | |||
| + | The title text brings in two more conditions: {{w|diplopia}}, or double vision, and {{w|myopia}}, or near-sightedness. Those who are near-sighted sometimes see distant objects more clearly while squinting. Then they would be able to see the one large number still visible from the synesthesia/colorblindness combination, but because of double vision they see a second copy of it, hence two numbers that are the same. | ||
| + | |||
| + | If we color the numbers in the circle in a consistent way (and leave the 2, 3, 5, 7 and 9s black) we can reveal the large numbers: | ||
| + | |||
| + | [[File:BLIQR6w.png|center]] | ||
| + | |||
| + | The numbers are four and two, forming the number {{w|42 (number)|42}}, which is the famous "{{w|Answer to the Ultimate Question of Life, the Universe, and Everything}}", according to the book {{w|The Hitchhiker's Guide to the Galaxy}}. The number 4 is formed by digits 2, 3, 5 and 7 (the single digit primes) while the number 2 is formed by digits 3, 5, 7 and 9 (the single digit odds, excluding 1). | ||
| + | |||
| + | For Randall's test to work (i.e. for either the large 4 or the large 2 in '42' to get lost in the noise to those with a given color-blindness), either the little number 2 or the little number 9 would have to be lost in the background noise. So, for example, if the background appeared in shades of red and the little number 2 was a shade of green, then the large number 4 would be less visible to those with red-green color-blindness than to others. | ||
| + | |||
| + | While it makes for a good joke, there are three reasons this kind of test wouldn't work in real life. | ||
| + | |||
| + | The first is that there is no one set of color-number associations seen by all synesthetes. So while some synesthete might see '2' as green and '0' as red (so a red-green color-blind person would lose anything made up of '2's against a background of '0's), others might see '2' as yellow and '0' as blue, or any other association imaginable. | ||
| + | |||
| + | The second reason it wouldn't work is that synesthetes do not (always) automatically see a 1:1 overlay of color on top of a number - they still need to read the number legibly. Randall's circle is very chaotic, so one wouldn't intuitively identify each single number. For a synesthete the color is produced ''after'' the number is recognized by the brain and lost when the focus shifts to the next number. However, some synesthetes may find if they pay attention to the numbers one by one they can make something out. However, as noted by a user in the discussion, who states that he has a type of synesthesia, he did indeed [http://otherthings.com/blog/2013/05/ishihara-eat-your-heart-out/#more-899 see the numbers]! Furthermore, in his blog's discussion section, one person commented they could [http://otherthings.com/blog/2013/05/ishihara-eat-your-heart-out/#comment-36822 see the large '2' but not the large '4']! This was not because the person was colorblind, but because the '4' was mostly composed of numbers ('2's and '7's) whose colors blended in with the background, while the '2' contained an even mix of numbers, some of which (presumably '3's, '5's, and '9's) starkly stood out, making the large '2' easily visible. However, one could easily imagine this scenario pertaining to colorblindness: for example, a colorblind synesthete, in theory (although the third reason makes it clear why this would be extremely unlikely), might perceive most of the background numbers as shades of green (similar to the picture below) and see the '2's and '7's in shades of red, which would make it difficult to differentiate between the giant reddish '4' and the greenish background. | ||
| + | |||
| + | The third reason the test would not work is that color-blindness is an inability to distinguish colors of light hitting the retina, it's nonsensical to imagine a synesthete would perceive two separate colors that they cannot normally separate anyway. But again in the above mentioned link this particular person did see the colors in a way where people with red/green color-blindness might have a harder time seeing the 4 than the 2 in 42. | ||
| + | |||
| + | The next image shows all of the numbers, including 2, 3, 5, 7 and 9, colored in, in such a way as to ensure the number 42 is clearly visible to those with no particular blue-yellow color-blindness: | ||
| + | |||
| + | The "real problem" is actually that if a synesthete does indeed see the digits as colors that resolve into either one or two numbers, then what color would these new "color-numbers" then appear to be? If a synesthete could see both large numbers AND they appeared as the same color as the small numbers as soon the synesthete perceived the numbers, then what would this meta-synesthete see? The '4' would blend in with the background '4's, while the '2' would stand out (as '2' was not used in the background). Would that mean that as soon as they noticed the giant '4', it would suddenly disappear into the background? Is this sort of layered synesthesia even possible? | ||
| + | |||
| + | [[File:combination vision test fullcolor.png|center]] | ||
| + | |||
| + | Keep in mind, as noted above, that synesthetes do not all see the same color-number associations. They also do not necessarily see every number in a different color, as depicted here, and may even see some numbers as purely black. | ||
==Transcript== | ==Transcript== | ||
| − | + | :[Caption above the drawing:] | |
| − | + | : Combination Vision Test | |
| − | + | ||
| + | :[Below the caption is a circle formed by several hundred numeric digits from 0-9.] | ||
| + | |||
| + | :[Caption below the panel:] | ||
| + | : If you can see one big number but not the other, you have synesthesia ''and'' colorblindness. | ||
{{comic discussion}} | {{comic discussion}} | ||
| + | |||
[[Category:Math]] | [[Category:Math]] | ||
Latest revision as of 21:10, 4 May 2022
| Combination Vision Test |
 Title text: If you see two numbers but they're both the same and you have to squint to read them, you have synesthesia, colorblindness, diplopia, and myopia. |
Explanation[edit]
Synesthesia is a condition in which perception in one sensory or cognitive pathway leads to automatic, involuntary experiences in a second sensory or cognitive pathway. Common examples are experiencing colors when seeing numbers or words (Grapheme-color synesthesia), hearing tones or music while reading words or text, seeing sequences of numbers or month names in a distinct and fixed shape (Number form), etc. In 1608: Hoverboard Megan stands at the end of the Star Destroyer and wishes she had synesthesia so bad she can taste it...
Color-blindness is one of a number of conditions in which a person cannot distinguish certain pairs of colors that other people without color-blindness might find easy to distinguish. There are many different forms of color-blindness; the most common is an inability to separate the colors red and green.
There are two numbers embedded in the big circle of numbers, in a similar way to a common color perception test. But this test can not work for colors because it is just a black-and-white picture. Nobody can see it. However, the joke lies in the fact that those with one common form of synesthesia see colors associated with numbers. Randall implies that a synesthete will see colors connected to each number, and thus a color perception test will work after all - thus distinguishing synesthetes with color-blindness from those with normal color perception.
The comic playfully suggests that if you have synesthesia as well as colorblindness, then some of the colors might appear identical and so one number would not be visible, only leaving the other number.
The title text brings in two more conditions: diplopia, or double vision, and myopia, or near-sightedness. Those who are near-sighted sometimes see distant objects more clearly while squinting. Then they would be able to see the one large number still visible from the synesthesia/colorblindness combination, but because of double vision they see a second copy of it, hence two numbers that are the same.
If we color the numbers in the circle in a consistent way (and leave the 2, 3, 5, 7 and 9s black) we can reveal the large numbers:
The numbers are four and two, forming the number 42, which is the famous "Answer to the Ultimate Question of Life, the Universe, and Everything", according to the book The Hitchhiker's Guide to the Galaxy. The number 4 is formed by digits 2, 3, 5 and 7 (the single digit primes) while the number 2 is formed by digits 3, 5, 7 and 9 (the single digit odds, excluding 1).
For Randall's test to work (i.e. for either the large 4 or the large 2 in '42' to get lost in the noise to those with a given color-blindness), either the little number 2 or the little number 9 would have to be lost in the background noise. So, for example, if the background appeared in shades of red and the little number 2 was a shade of green, then the large number 4 would be less visible to those with red-green color-blindness than to others.
While it makes for a good joke, there are three reasons this kind of test wouldn't work in real life.
The first is that there is no one set of color-number associations seen by all synesthetes. So while some synesthete might see '2' as green and '0' as red (so a red-green color-blind person would lose anything made up of '2's against a background of '0's), others might see '2' as yellow and '0' as blue, or any other association imaginable.
The second reason it wouldn't work is that synesthetes do not (always) automatically see a 1:1 overlay of color on top of a number - they still need to read the number legibly. Randall's circle is very chaotic, so one wouldn't intuitively identify each single number. For a synesthete the color is produced after the number is recognized by the brain and lost when the focus shifts to the next number. However, some synesthetes may find if they pay attention to the numbers one by one they can make something out. However, as noted by a user in the discussion, who states that he has a type of synesthesia, he did indeed see the numbers! Furthermore, in his blog's discussion section, one person commented they could see the large '2' but not the large '4'! This was not because the person was colorblind, but because the '4' was mostly composed of numbers ('2's and '7's) whose colors blended in with the background, while the '2' contained an even mix of numbers, some of which (presumably '3's, '5's, and '9's) starkly stood out, making the large '2' easily visible. However, one could easily imagine this scenario pertaining to colorblindness: for example, a colorblind synesthete, in theory (although the third reason makes it clear why this would be extremely unlikely), might perceive most of the background numbers as shades of green (similar to the picture below) and see the '2's and '7's in shades of red, which would make it difficult to differentiate between the giant reddish '4' and the greenish background.
The third reason the test would not work is that color-blindness is an inability to distinguish colors of light hitting the retina, it's nonsensical to imagine a synesthete would perceive two separate colors that they cannot normally separate anyway. But again in the above mentioned link this particular person did see the colors in a way where people with red/green color-blindness might have a harder time seeing the 4 than the 2 in 42.
The next image shows all of the numbers, including 2, 3, 5, 7 and 9, colored in, in such a way as to ensure the number 42 is clearly visible to those with no particular blue-yellow color-blindness:
The "real problem" is actually that if a synesthete does indeed see the digits as colors that resolve into either one or two numbers, then what color would these new "color-numbers" then appear to be? If a synesthete could see both large numbers AND they appeared as the same color as the small numbers as soon the synesthete perceived the numbers, then what would this meta-synesthete see? The '4' would blend in with the background '4's, while the '2' would stand out (as '2' was not used in the background). Would that mean that as soon as they noticed the giant '4', it would suddenly disappear into the background? Is this sort of layered synesthesia even possible?
Keep in mind, as noted above, that synesthetes do not all see the same color-number associations. They also do not necessarily see every number in a different color, as depicted here, and may even see some numbers as purely black.
Transcript[edit]
- [Caption above the drawing:]
- Combination Vision Test
- [Below the caption is a circle formed by several hundred numeric digits from 0-9.]
- [Caption below the panel:]
- If you can see one big number but not the other, you have synesthesia and colorblindness.
Discussion
Number is "42". The 4 is composed of 2's and 3's and 7's. The 2 is composed of 3's and 7's and 9's. --RainbowDash (talk) 05:16, 17 May 2013 (UTC)
- What about 7s? --81.23.24.34 06:13, 17 May 2013 (UTC)
Also both have 5's. I'm not very good at this counting thing. That link below is way better, anyhow. --RainbowDash (talk) 05:28, 17 May 2013 (UTC)
http://i.imgur.com/BLIQR6w.png
Credit: http://www.reddit.com/user/silly-moose
I'm not confident enough about this to write up an explanation, but given that synesthesia is a sensory experience where the senses blend into each other (hearing colors, tasting sounds, etc...) that a round shape or black and white (why is it not in color? that would help the joke imho) give the sense of a number to the synesthete. The alt text at least makes sense, seeing two big numbers fits with diplopia (double vision) and the squinting covers myopia (nearsightedness) so it is consistent with the main joke, but I feel like I'm really missing something in the main joke. Chexwarrior (talk) 06:43, 17 May 2013 (UTC)
In the original b&w image, I keep seeing an 8 on the right and a vague 0, 9, or 4 on the left. I'm not certain if the b&w actually has a definite "answer" or specific number(s) one is supposed to be seeing. I seem to recall an xkcd with an Ishihara test before (but can't find it so it may just be a confabulation), in which case this one may be a reference to that and actually have a referential "answer".
I'm not an optometrist, but Chexwarrior,'s explanation of the alt text seems correct to me. Plazma (talk) 07:00, 17 May 2013 (UTC)
On the left half, the number 9 is missing. Similarly, on the right the number 2 is missing. This makes the number 92 or 29 (any ideas?). There is a floating 2 in the bottom center, the origin is unknown but it does look like a decimal point but that yould defeat the purpose of the number 42 (any ideas?) --Zom-B (talk) 07:06, 17 May 2013 (UTC)
- There is also a floating 4 on the left. ConscriptGuide (talk) 18:22, 9 August 2023 (UTC)
I was thinking the explanation of the descriptive text (not alt-text) is as follows: the synesthesia is seeing numbers and associating colors with them. So when you look at the numbers in the image, you see certain colors, so the large numbers stand out because they are different colors from the background. But if you're colorblind, (hypothetically) then some of those number-colors might look the same and so the numbers (not sure why only one) would not be visible. Bplimley (talk) 07:18, 17 May 2013 (UTC)
- Maybe if the synesthesia is as follows: Even numbers get one color and odd numbers get another color. I was actually able to see the 2 because of this effect, while I was in photoshop, zoomed in, and coloring the 3's. I know from myself that I have number to color synesthesia, but (in my case) that doesn't apply to a bunch of randomly placed digits like here, but only to complete numbers like "144" looks yellow, red, and white (in no particular order), while "38" looks grayish dark blue. --Zom-B (talk) 07:22, 17 May 2013 (UTC)
- I seriously doubt ANYONE have so "hard" case of number to color synesthesia it can "color" a bunch of randomly placed digits like this. Like ... if your number-recognizing neurons are working on the small numbers, how can they work on the big numbers in the same time? -- Hkmaly (talk) 09:01, 17 May 2013 (UTC)
- Good catch! I'm not sure how exactly how synesthesia works, but even if the perceived number (due to a perceived colour) further incites a perceived colour, you can still have a combined diagnostic. You just have to make sure that the big number is made up of little ones of the same number; or, atleast made of other numbers which are of the same colour as the desired big number. The latter requires that you assume synesthesia is one way only (for instance - perceiving number triggers colour, but not vice versa) 220.224.246.97 11:00, 17 May 2013 (UTC)
- No no, it pretty much works! I've got colored-grapheme synesthesia, and while the numbers don't jump out at me as easily as they would if they were made of real colors, I am able to see them pretty clearly if I lean close enough to my monitor to be able to take in all of the small numbers' shapes at once. I posted a description of what it looks like to me here: Rungy Chungy Cheese Bees It's a bit harder for me to see because I'm an "associator" type of synesthete, as opposed to a "projector" type. But I imagine for a true projector synesthete this would be about as easy as a normal Ishihara colorblindness test. Otherthings (talk) 20:35, 17 May 2013 (UTC)
- It didn't work at all for me. I've got coloured-grapheme synesthesia too, but all the colours were too different - I have no real pattern for even and odd numbers, so I never saw the big numbers. I looked at your link, you got a nice contrast! 121.219.96.178 02:29, 4 June 2013 (UTC)
<Nitpicking> The alt text is slightly off the mark isn't it? Wouldn't a diplopic(?) person see two images of the diagnostic rather than two numbers in the same diagnostic? Also, you needn't be colour blind to fulfill the condition of perceiving only one digit. Your synesthesia might have a colour blindness, while your optical system does not. </Nitpicking> 220.224.246.97 11:07, 17 May 2013 (UTC)
I think that as no two... synaesthetes? ...have exactly the same 'conversion routine' in place that one can't assume the colour dominance of either digit, under an (actual, or synaesthetic) colour-blindness condition. Also, I wouldn't be surprised to hear "Well, the left hand side smells a bit like a 4, but the right sounds like a 2..." ;) 178.98.207.61 12:54, 17 May 2013 (UTC)
I will take some LSD and look at this and report back later! 46.166.163.150 16:22, 17 May 2013 (UTC)
I don't think myopia actually makes sense, unless you're reading the comic on a large screen 30 or 40 feet away. The comic is most probably near you, if you're near-sighted you should see it in focus without squinting. 64.223.217.58 17:19, 17 May 2013 (UTC)
- As a myopic person, I can say that you are generalizing too much. Without glasses, I can see no thing in focus unless it is 2-4 inches from my face75.69.96.225 20:22, 17 May 2013 (UTC)
I see a big zero!
In the end this test couldn't work, colorblindness is due to a physical effect in the eyeball where synesthesia works in the brain, if someone had both synesthesia and colorblindness then the two numbers in the circle above would be the _only_ color they could see (although being colorblind they may not understand it to be a color at that point) Odysseus654 (talk) 19:37, 17 May 2013 (UTC)
- It's a JOKE. Sure it does not work for many more reasons. But the combining of all this things is hard to understand and it did last a couple of hours until the first people did understand. In my opinion this is one of the BEST jokes Randall ever did.--Dgbrt (talk) 19:47, 17 May 2013 (UTC)
- Yah, I laughed pretty hard when I saw it last night. Still worth explaining all the intracacies, like people wondering what's wrong with "Locate City" nukes Odysseus654 (talk) 20:10, 17 May 2013 (UTC)
- Actually, there's research on that. People with colorblindness and synesthesia do "see" some numbers in colours that they don't recognise from their everyday experience. (That's because as you said, colorblindness happens at the receptor level and synesthesia happens in the brain). Check out this TED talk: http://www.ted.com/talks/vilayanur_ramachandran_on_your_mind.html?quote=222 --- Mel
- Sorry, wrong link. I meant this talk: http://www.youtube.com/watch?v=WW_lsSx5w14 --- Mel
- I am not colourblind and my synesthesia STILL gives me colours that don't exist, so I'm sure colourblind people's colourblindness wouldn't necessarily translate to their synesthesia. 121.219.96.178 02:29, 4 June 2013 (UTC)
As a colorblind person, I would like to point out that it is not obvious to everybody that a normal person sees neither large number. At first glance, I assumed that normal people see both numbers, colorblind people see neither, and synthesesia allows colorblind people to see one.75.69.96.225 20:22, 17 May 2013 (UTC)
- No, even normal people can't see the numbers because the image is just black and white. But that's just the first joke. Synthesesia in this comic just do see colours on black and white pictures.--Dgbrt (talk) 20:36, 17 May 2013 (UTC)
- Shouldn't the big-4 and big-2 have it's own color? The big-4 might then blend with the background 4's.
- What's with the extraneous little-2 underneath the big numbers also?50.8.61.60 21:32, 17 May 2013 (UTC)
- Shouldn't the big-4 and big-2 have it's own color? The big-4 might then blend with the background 4's.
I'm not convinced that this cartoon works. I have a friend who is synaesthetic, and she can't see the big numbers. The thing is, if someone has the sort of synaesthesia where they see numbers in colours, then they see each digit in a different colour, and so there is no reason why primes (or any other particular group of digits) would stand out for them. Yes, I know it's a joke, but the joke doesn't work if it doesn't take into account how synaesthesia works.
- I might do some fiddling with various colour palette overlays, but I think that if there is a large cluster of a few colours which don't appear elsewhere in the image, the synaesthete could probably pick up the pattern. However, the actual function of synaesthesia is not really important in this, I suppose. 86.14.71.242 (talk) (please sign your comments with ~~~~)
I saw the number 12 without checking here first, and I'm not a synesthete. Anyone see something similar? 71.176.19.228 00:13, 18 May 2013 (UTC)
- Reading it on an iPad, by zooming right out, I can get occasional brief flashes of the number while moving my eyes - though I initially read it as 92, probably because I couldn't look directly at it. I can't work out what it is that makes it jump out at me, though - maybe my eyes are catching the pattern of sevens, or something? --123.243.65.31 09:43, 18 May 2013 (UTC)
- I also read it as 92, but without any tricks. Just by painfully staring at the image my brain makes out lines and curves, till i found the 92. Is that normal? :D 88.70.142.19 13:23, 18 May 2013 (UTC)
- I can see the 2 vaguely (probably because the numbers making it up are a bit smaller and denser), and would have said "92" too, but only at gunpoint. So it IS normal. Wait, I'm not normal :D 108.162.230.137 11:33, 21 July 2014 (UTC)
- I also read it as 92, but without any tricks. Just by painfully staring at the image my brain makes out lines and curves, till i found the 92. Is that normal? :D 88.70.142.19 13:23, 18 May 2013 (UTC)
In the last image, I think it would be better to have the background, the 4, and the 2 be made of different shades of 3 different colors to make it clear why someone who is colorblind would only see one of the numbers. Say, the background is different shades of green, the 4 is blue, and the 2 is red. That is, if I'm understanding this comic correctly. 184.170.166.111 07:43, 18 May 2013 (UTC)
This would be incredibly confusing to a synesthete. Wouldn't he/she see the big 4 and 2 as being colors of their own? And then, of course, its component numbers would be made of so many different colors. I think we need a real synesthete to look at this. 71.176.19.228 15:11, 18 May 2013 (UTC)
- I have heard from real synesthete people that there are too many chaotic numbers on the picture. I did add an explanation on the bottom of the main page. --Dgbrt (talk) 14:37, 19 May 2013 (UTC)
- I experience the same. But what about User:Otherthings who claims he sees all colors at once. Different synesthesia or fake? Also, when examining numbers to invoke colors, you forget past colors, unless the subject has a photographic memory and won't lose the colors? Even then s/he still needs to look at every single digit in the image in individually. --Zom-B (talk) 08:03, 20 May 2013 (UTC)
- I think you're the closest to right. I have sound-to-image synesthesia, so when I hear a sound, it brings to mind a certain image. However, this image is only in my mind's eye. And as I've gotten older, I've become less able to hold on to that image in my head. The images follow a sort of dream logic. Anyway, even though I have a different type of synesthesia, it stands to reason that this type should work similarly. It seems to me that they would, when reading each digit, get an impression or be reminded of the corresponding color. --108.162.216.36 00:31, 19 January 2014 (UTC)
- I experience the same. But what about User:Otherthings who claims he sees all colors at once. Different synesthesia or fake? Also, when examining numbers to invoke colors, you forget past colors, unless the subject has a photographic memory and won't lose the colors? Even then s/he still needs to look at every single digit in the image in individually. --Zom-B (talk) 08:03, 20 May 2013 (UTC)
What does it mean if I can see multiple giant numbers? When I looked at this, I immediately saw a giant 58 - and had no idea what 58 was supposed to mean. Then I could see other numbers as well, of varying mixed sizes.
PLEASE understand that this Black and White "color perception test" can not work. Nobody can see that Big Numbers. And this is just only the first part of this joke.--Dgbrt (talk) 23:00, 23 May 2013 (UTC)
I think it should say "one digit" or "two digits", rather than one or two "numbers", as 42 is just one number (consisting of two digits), though of course it _could_ be read as the two numbers 4 and 2, that just happen to be placed next to each other. I know this is less important when it doesn't actually work :P
In response to people saying no one can see the big numbers - I saw them easily. I don't have any particularly special condition, though (that I know of), but I saw the '42' before I even read the caption. It jumps out at me whenever I shift my point of focus slightly. Surely I'm not the only one? 141.101.98.251 04:53, 28 September 2014 (UTC)
I saw this asked a few places so: I see different colors for letters and words (c, a, t and cat have unrelated colors) and similarly for numbers. So I would see the same color for big and little twos but different colors for the other components. No contradiction here, it just depends on what I'm focusing on. 172.70.42.167 05:26, 7 March 2024 (UTC)