1230: Polar/Cartesian
| Polar/Cartesian |
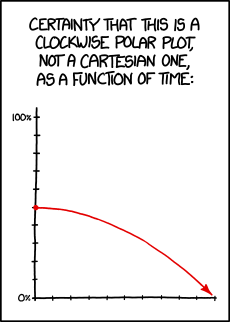 Title text: Protip: Any two-axis graph can be re-labeled 'coordinates of the ants crawling across my screen as a function of time'. |
Explanation[edit]
This comic plays upon the difference between reading a polar coordinate plot and the more common Cartesian coordinate plot.
The graph purports to show the certainty in the viewers mind that it is a clockwise polar plot, as a function of time.
If seen as a Cartesian plot, the y (vertical) axis represents 'certainty' while the x (horizontal) axis represents 'time'. Each point on the plot is represented by two coordinates, the x-value and the y-value. As time increases, we move to the right and see the initial certainty of 50% decreases gradually to zero. That is, after a certain amount of time, we are certain that it is NOT a polar plot.
In a polar plot, each point on the plot is also located by two values, but in this case they are the radius (the distance from the origin) and the angle between the radius and an arbitrary starting line. Here, the radius represents 'certainty' and the angle to the vertical represents 'time'. In this view, we see that as time increases (as we move clockwise around the plot) the initial certainty (the same 50%) now increases to a final value of 100%. That is, after a certain amount of time, we are certain that it IS a polar plot.
The intended joke seems to be that the graph is an exercise in confirmation bias. Whichever type you initially hypothesize is correct, that view will be confirmed by investigation. This is because the two different views are both correct - the graph can equally be considered a Cartesian or polar plot. This is somewhat counter-intuitive.
Throughout the graph, the sum of the two probabilities is 100%, i.e. (polar-observer's certainty that the graph is polar) + (Cartesian-observer's certainty that the graph is polar) = 100%. The shape of the graph appears to be (in clockwise polar form) r(t)=100/(1+cos(t)).
If the reader is open-minded, they would never reach certainty (0% / 100% depending on how you read the graph) because there isn't enough information to clearly decide either way.
The title text is a joke that if you are unsure how to label any two-axis (two-dimensional) graph, you can just say it represents the 'coordinates of the ants crawling across my screen as a function of time', and nobody could then argue with your data. "Hey, that's the path they walked!"
Transcript[edit]
- [Caption above the panel:]
- Certainty that this is a clockwise polar plot, not a Cartesian one, as a function of time:
- [There is a graph. The Y axis is marked out from 0% to 100%. The X axis is unmarked. A red line starts at 50% and traces out a roughly parabolic trend downwards along the X axis.]
Discussion
Heh. Schroedinger's graph. Simultaneously 100% certainty of being Cartesian and 100% certainty of being Polar. 12.117.213.34 09:03, 26 June 2013 (UTC)
If you take into account 833, this graph shows certainty that you are interpreting it correctly. --DiEvAl (talk) 09:48, 26 June 2013 (UTC)
The ambiguity is due to the unlabelled x-axis. --Prooffreader (talk) 10:48, 26 June 2013 (UTC)
The title text protip is really only applicable to 2 axes continuous graphes, unless you count ants being added or flicked away by the user as discontinuities. 24.247.120.53 13:07, 26 June 2013 (UTC)ProfKrueger
The shape of the graph appears to be (in polar form) r(t)=100/(1+sin(t)), which I solved for using the constraint that r + y = 100, or rather (polar-observer's certainty that the graph is polar) + (cartesian-observer's certainty that the graph is polar) = 100%. The two observers become further entrenched in their own ideologies as time goes on, and at equivalent rates of entrenchment. 98.197.196.242 16:25, 26 June 2013 (UTC) DAF
The title text is, well, wrong. To plot coordinates "as a function of time" you would need THREE-axes. JamesCurran (talk) 19:23, 26 June 2013 (UTC)
- No, we have a radius (from the zero point to the red line), we have an angel (from 0° to 90°), and we have a point moving along that red line by time. A single (not moving) ant would just be a (red) point.--Dgbrt (talk) 20:56, 26 June 2013 (UTC)
- No, a two-dimensional red line does not contain information on which direction the ant is moving and at what velocity (well, actually, the ant is where the red line ends), but the point is that you cannot plot a red ball falling to the ground from 100% to 0% height "as a function of time" using a single axis.176.226.42.80 05:37, 27 June 2013 (UTC)
- There is a third dimension. It is time itself. Ants unlike ink can move along that axis. However my interpretation takes liberties with the definition of graph.12.198.205.9 23:01, 11 July 2013 (UTC)
- No, a two-dimensional red line does not contain information on which direction the ant is moving and at what velocity (well, actually, the ant is where the red line ends), but the point is that you cannot plot a red ball falling to the ground from 100% to 0% height "as a function of time" using a single axis.176.226.42.80 05:37, 27 June 2013 (UTC)
- The title doesn't say anything about coordinates. The axis is "certainty", which is a scalar value. --108.162.216.8 16:34, 28 June 2014 (UTC)
- I'm late, but... https://en.wikipedia.org/wiki/Parametric_equation 162.158.78.82 01:27, 11 February 2017 (UTC)
I like this comic. But I think "subjective probability" or "degree of belief" might be better than "certainty", because 0% certainty that it's polar is not 100% certainty that it's not polar. I think 0% certainty means that you have no pertinent information, and might as well flip a coin. Also, switching it to be self-refuting rather than self-confirming would also be funny. --Clay
- Incomplete tag
I did add this tag just because we have a chaos at explanation here. So I will try to simplify but I will also need your help, maybe discussed here at talk first.--Dgbrt (talk) 21:46, 26 June 2013 (UTC)
- Transcript is biased?
"[The graph shows a red curve starting at 50% on the Y-axis and arcing down to intersect 0% at the 10th unit of the X-axis.]" That seems judgemental as to which kind of graph it is. Without misquoting Word Of God in any way is it possible to instead make changes something like "...starting at 50% in the direction represented by the vertical axis and either arcing down to [...] the horizontal-axis or spiraling outwards to 100% by the radial angle represented by this perpendicular." But perhaps less verbose, if someone has the verbal skills required to accomplish this. (Also, transcript does not mention the arrow, at all, with its possible significance. It could be just treated as an idle temporal indicator, regardless of graph-type, although it has strong associations with polar graphing, as mentioned.) 178.98.31.27 05:09, 27 June 2013 (UTC)
- The comic had no internal transcript, so I made one up. I just changed it again to try and be as unbiased as possible. If it's still confusing or biased or whatever, take a shot at fixing it yourself. :) --Druid816 (talk) 06:06, 29 June 2013 (UTC)
- Is this it?
The similarity is probably just a coincidence, but Comic 1230 reminded me of the middle one of these curves. Its polar equation simplifies to r = pi - 2 arctan(sin(theta)). If a rotational motion in three dimensional space has constant angular velocity, its angular displacement (aka axis-times-angle) traces one of the curves in this family.
Buster (talk) 21:44, 1 July 2013 (UTC)
- Thanks Buster for signing in here and presenting this graphic. But I am still pretty sure Randall did not thought about "pi - 2 arctan(sin(theta))", he was just observing some ants (or flies) on his screen. Sometimes the world is so simple, while the explanation is covered in complex analogies, Randall is doing this often. I like this plot, but I am sure this plot was not in mind of Randall when he did draw this comic.--Dgbrt (talk) 22:07, 1 July 2013 (UTC)
- Incomplete tag again
The explain is incorrect and misleading for the "time" value. We should explain this by using Randalls ant example from the title text:
- At Cartesian coordinates an ant is a dot, when it moves by time we will get more dots or just a line. So there are three values at the plot: x-location, y-location, and the time which shows the move.
- On polar coordinates the difference is that we have only one axis, this is the radius or the distance from the zero point. The second coordinate is the angel to an arbitrary axis. A single position of an ant is again still just a dot. If the location changes by time we also do get a line.
The arrow just shows the direction for the time value.
There are many more polar plots like antenna side lobes, but the plot at this comic is much more simple.--Dgbrt (talk) 19:32, 3 July 2013 (UTC)
The explanation gives the equation as r(t)=100/(1+sin(t)). When t=0, r should be 50 because this is a *clockwise* polar graph, so this function isn't right. The correct equation is r(t)=100/(1+cos(t)).108.162.216.30 02:46, 3 June 2015 (UTC)

