1270: Functional

|< < Prev Comic #1270 (September 27, 2013) Next > >|

Functional

Title text: Functional programming combines the flexibility and power of abstract mathematics with the intuitive clarity of abstract mathematics.

Explanation

White Hat questions Cueball's faith in functional programming. Cueball responds saying, "Tail recursion is its own reward."

Functional programming is a paradigm of computer programming with roots in Lambda Calculus. Core tenets of functional languages often include: function application and composition, declarative syntax, immutable data structures, and mathematically pure functions. Functional programming often uses recursive functions to serve the same purpose that loops serve in other programming languages. A recursive function calls itself again, typically with slightly different arguments. E.g., the following factorial function is recursive because it calls itself again for any argument value n greater than 0.

factorial(n):
    if n == 0:
        return 1
    return n * factorial(n-1)

Tail recursion is a particular sort of recursion that often compiles into more efficient code (see the longer explanation below), but the differences between tail recursion and other sorts of recursion aren't important to the humor of this comic.

The comic is a pun on two readings of "Tail recursion is its own reward". The expression "X is its own reward" often is used to suggest that X is intrinsically valuable in its own right. Some (but not all) programmers and mathematicians find recursive functions elegant and intrinsically pleasing, so would take tail recursion to be its own reward in this sense. Since recursive functions call themselves again, and make use of the resulting values, there is also a sense in which recursive functions also serve as their own "reward" - i.e., the recursive function itself returns the values that the function requires to perform its tasks. So even if you don't find tail recursion intrinsically pleasing, there is still this technical sense in which it is its own reward anyway.

The title text is humorous in part because it violates two expectations. First, expressions of the form "X combines some trait of Y with some trait of Z" usually talk about combining traits of two different things (i.e., Y is not equal to Z) whereas this text surprises the reader by having "abstract mathematics" occupy the role of both Y and Z. And second, such expressions usually list two positive traits. The first listed trait (the "flexibility and power of abstract mathematics") is pretty clearly positive. However the second trait (the "intuitive clarity of abstract mathematics") is less clearly positive. Many people actually find abstract mathematics to be quite lacking in intuitive clarity, and for much the same reasons many people often find functional programming also to be lacking in intuitive clarity. So the title text invites the reader to puzzle over whether it really is a positive thing for functional programming to be able to claim to match the "intuitive clarity of abstract mathematics", or whether Randall might instead have just smacked functional programming with a funny backhanded compliment. Another explanation is that the fact that that part of the title text is confusing is a metaphor for the fact that abstract mathematics and functional programming can be confusing, and the first part of the title text is flexible because it can be applied to a wide variety of situations with different things filling in the blanks for X, Y, and Z, and it's apparently powerful because it's used in marketing a lot,^{[citation needed]} so advertisers must feel that it will have a powerful effect.

Further explanation

Functional programming is a famous paradigm (or style) in modern programming that favors functions that can be evaluated like mathematical functions, i.e., functions are "evaluated" (executed) to return a value (their output) which exclusively depends upon the values of their arguments (their inputs). Imperative programs, by contrast, often make use of one or more variables that are external to the function that is currently executing. This means that an "imperative function" may return a different result for the same input due to changes in a non-local variable, whereas a "pure function" will always return the same result for a given input; however, in practice some functional programming languages also support non-local variables.

Additionally, for similar reasons, functional programming systems often strive to eliminate or at least rigorously encapsulate (contain) so-called "side effects"; i.e., "functional-style" functions should have absolutely no effect on anything other than their return value. This is to say, in well-designed "functional-style" computer code, all functions, or as many as is practicable, should be stringently self-contained, their behaviour should depend entirely and exclusively upon their written definition and the values of their arguments, and they should be totally unable to affect anything else in the program except via their explicit return value.

This is directly contrary to the imperative programming paradigm, where functions are often designed and invoked especially for some ulterior effect that will eventuate when they are executed; some "imperative-style" functions even have no return value, and exist purely because running them is known to cause some other desired result. In functional programming, these are not considered functions at all, but rather "procedures", and the difference between functions and procedures is quite strong; some languages which are purely functional do not admit procedures as valid parts of the language at all.

Unlike procedures, functions always return a value. For example, sine(x) returns 1 when x is 90°. Furthermore, the function may call itself (usually with slightly different parameters), thus effectively starting a loop. This is called recursion.

In order to iterate, imperative programs usually use loops. Functional programs usually use recursion instead.

For example, the factorial function (e.g. "factorial(5) = 5 x 4 x 3 x 2 x 1") can be coded imperatively as:

factorial(n):
    prod = 1
    while n > 0:
        prod = prod * n
        n = n - 1
    end
    return prod

An imperative, recursive (but not tail-recursive) implementation can look like this:

factorial(n):
    if n > 0:
        return n * factorial(n-1)
    else:
        return 1

In this situation, the recursion stops when the argument (n) is not greater than zero. Without the conditional definition, it would be an infinite loop. Tail recursion is a special case of recursion whose very last operation is to invoke the function itself or return a definite value. The previous example is not tail-recursive, since after the call to "factorial(n-1)", the returned value has to be multiplied by n.

This (functional) example is tail recursive inside the helper function:

factorial(n) = factorial_helper(n, 1)

factorial_helper(n, prod) = 
    if n > 0 then
        factorial_helper(n - 1, prod * n)
    else
        prod

e.g.

factorial(5) = factorial_helper(5, 1)
 factorial_helper(5,1) = factorial_helper(5-1, 1*5)
  factorial_helper(4,5) = factorial_helper(4-1, 5*4)
   factorial_helper(3,20) = factorial_helper(3-1, 20*3)
    factorial_helper(2,60) = factorial_helper(2-1, 60*2)
     factorial_helper(1,120) = factorial_helper(1-1, 120*1)
      factorial_helper(0,120) = 120

In functional programming, tail recursion is detected by the compiler or interpreter and can be executed as efficiently as loops in imperative programming languages. This makes tail recursion an essential programming technique in functional programming.

Cueball is making a play on words where "Tail recursion is its own reward" is used both in the sense that it is worth doing on the grounds of being elegant and intellectually satisfying alone, without the programmer having to "actually get" anything from it, as well as in the sense that the 'tail call' of a function is its final step, and is the final step (and hence the result/reward) for all levels of a tail-recursive function.

The title text suggests that to the mathematically minded functional programming may be both powerful and flexible as well as intuitive and clear since it very closely approximates the way mathematicians ordinarily think about general recursive functions. The implicit humorous contrast is that, to many (possibly most) others, including many software engineers, functional programming can seem abstruse or highly unobvious for the exact same reason, because it closely approximates abstract mathematical logic rather than the mechanistic, stepwise logic valued in the imperative programming style. It is also a reference to a common saying among functional programmers about the imperative programming language, 'C': "C combines the flexibility and power of assembly language with the user-friendliness of assembly language", which is a humorous take on the original saying "C combines the flexibility and power of assembly language with the user-friendliness of a high-level language".

Transcript

[White Hat stands behind Cueball, who is sitting at a computer.]

White Hat: Why do you like functional programming so much? What does it actually get you?

Cueball: Tail recursion is its own reward.

 add a comment! ⋅  add a topic (use sparingly)! ⋅  refresh comments!

Discussion

Am i the only one considering this can be presented also in opposition to Object Oriented Programming, where tail recursion is very difficult to achieve at execution time, and impossible to achieve at compilation time, due to the possibility of method overloading?193.190.231.132 15:17, 30 September 2013 (UTC)

Since tail recusion is special case of tail call you don't need to know where the last function called goes - you just replace call by jump - if you don't know where by indirect jump. AFAIK both clang and gcc are doing it and in FP this gives the 'continuation passing style' of programming. The problem with it is that you loose the stacktrace so usually it is done only for optimized builds. 199.27.130.234 06:41, 26 October 2014 (UTC)

I'm getting the adblock message at the top.. on mobile. On an unrelated note, I laughed and I don't even get it. Edit: I'm also seeing an ad while seeing the message.50.159.5.112 06:03, 27 September 2013 (UTC)

This shouldn't be in comic discussion. I have written an updated version of our ad plugin that should only display a message to people using adblock, but we're using a sitenotice for now to test the waters. We'll take it down in about a day, promise!

Also, would you be complicit if I were to move this to the relevant forum? Davidy²²[talk] 06:13, 27 September 2013 (UTC)

I removed that misguided explanation about lists that was not tail recursive. I'm also wondering if we should also mention that tail call optimization is also applicable to mutually recursive functions. In fact proper functional languages will always apply it whether the functions are recursive or not. Maybe emphasize the fact that "The efficiency and elegance are the literal rewards of tail recursion."?

I feel like the examples should be in Haskall[sic], because that is the major functional language... 67.160.98.42 09:48, 27 September 2013 (UTC) GBGamer117

I think Haskell is more common, but I agree. And to emphasize the clarity, usually if/else blocks are avoided using pattern matching. I.e. tail-recursive factorial can be written as follows:

 fac2::Integer->Integer-> Integer  -- optional function header
 fac2 acc 0 = acc
 fac2 acc n = fac2 (acc*n) (n-1)
 
 fac::Integer-> Integer
 fac = fac2 1

--Chtz (talk) 10:34, 27 September 2013 (UTC)

Addendum: I did not dare to edit that yet, as I am unsure if this actually helps anyone not familiar with functional programming (and I don't think this page should include a Haskell crash course just to explain this comic). --Chtz (talk) 10:43, 27 September 2013 (UTC)

I think the pseudo-code examples currently in the explanation are easy enough to understand regardless of which programming languages one works in, but the [I'm assuming] Haskell example here in the comments makes no sense to me. Saibot84 12:51, 27 September 2013 (UTC)

Even though they are as clear and intuitive as abstract mathematics ... We could write it in a pseudo-functional language like this:

 fac2(acc,0):=acc;
 fac2(acc,n):=fac2(acc*n,n-1)
 fac(n):= fac2(1,n)

The main point of the functional programming paradigm is not that all functions return values (as currently stated in the explanation) but that functions don't have side-effects and don't have an internal state (i.e. they can have parameters, but they don't have variables). This makes recursion the only way to implement things which are usually implemented using loops in procedural languages. Tail-recursion has the benefit that it can be optimized very easily. --Chtz (talk) 21:18, 28 September 2013 (UTC)

I thought about the text a little and don't the the interpretation "tail recursion is an end unto itself" is correct. I think what's going on is a pun of the word "reward". "Tail recursion is it's own reword" makes more sense since you are calling the same function but are "rewording" the arguements. To reword means to re-express something with different words. --24.187.72.209 11:31, 27 September 2013 (UTC)

Why would you start a wall of text with TL;DR? Doesn't that belong at the end, followed by a very short synopsis? Smperron (talk) 13:17, 27 September 2013 (UTC)

Oy, this explanation doesn't actually explain anything. To start with, it needs a definition of "functional programming". Also, a single example of recursion should be plenty: this isn't a programmer's textbook. I really, really don't understand the reward/reword "pun" (if it is such a thing); is the "reword" version really in current use in functional programming circles? If it is, you need to highlight the o vs. a difference (bold and underline) to make it pop out - it took me four readings to notice it. Unfortunately, I don't understand these topics enough to even begin to edit the explanation. (Smperron is right: TL;DR belongs at the end, not the beginning, and it really can't be followed by a wall of text like this.) 108.36.128.166 14:52, 27 September 2013 (UTC)

"tail recursion is its own reword" - The only instance of this on Google is this page. Searching for tail recursion reword on Google also yields no results on the first page that agree with the proposed usage in functional programming circles. I think the pun explanation should be taken out, as it's clearly wrong. -- 67.170.217.103 15:55, 27 September 2013 (UTC)

I wasn't happy with the pun line this morning, and worked out what was niggling me earlier this evening, so I changed it to point out that the 'tail call' of a 'tail recursive' function is the end for *all* the invocations. That seems punnier to me. SleekWeasel (talk) 22:17, 27 September 2013 (UTC)

So.... can someone explain why the recursion code examples are written in Python? Schiffy (Speak to me|What I've done) 13:30, 28 September 2013 (UTC)

Why not? While python doesn't eliminate tail recursions (i.e., it lacks the optimization mentioned in the explanation) it is well suited to illustrate the idiom/pattern. Even though there's little reason to use the pattern in python, one can show how it'd look like.

In my experience, simple python code can easily be read (often correctly!) by programmers not knowing that language, which cannot be said about many functional languages. Therefore I tend to say that "python is executable pseudo-code", which makes it perfect for explanatory examples. (Unlike actual pseudo-code, it has well-defined semantics, but like pseudo-code, it's mostly readable for programmers not knowing its exact syntax.) --Das-g (talk) 15:01, 28 September 2013 (UTC)

I changed the functional examples to functional pseudo code. In imperative programming languages it rarely makes sense to write tail recursive functions using recursion instead of a loop. (Sure, there are cases, but factorial is not one of them) --Chtz (talk) 23:42, 28 September 2013 (UTC)

Title text

The title-text explanation is not quite right in my opinion. The joke is that abstract mathematics is not intuitive or clear to *anyone*, including mathematicians. Functional programming borrows many concepts from higher-level mathematics, so understanding the concepts behind functional programming often requires an abstract mathematical mind.

In other words, the title-text explanation is wrong because it claims that a contrast is being drawn between mathematicians and non-mathematicians. This is not the case (at least by my interpretation).

27.32.32.199 12:01, 29 September 2013 (UTC)

Being a mathematician, I can't agree. Even though I would consider myself more an applied mathematician, I find the basic concepts of abstract mathematics quite clear and intuitive (at least to a level which is required to understand functional programming). I do agree that there are many areas of abstract mathematics neither intuitive nor clear to me, but I am quite sure for people working in these areas this is not the case. --Chtz (talk) 21:06, 29 September 2013 (UTC)

sinus(X)?

In English math, it's sin(x) as an abbreviation for sine of x -- is sinus something specific to programming, or is it just a typo? 50.23.115.122 (talk) (please sign your comments with ~~~~)

I'm not native English, but sine or just sin in programming is correct. Thanks for your help.--Dgbrt (talk) 17:56, 29 September 2013 (UTC)

I'm not sure if sine(x) is any good example at all. It is a function, but as I tried to explain below, that does not make it relate to functional programming. And I would say that sine(pi/2)=1 and sine(90) is approximately 0.894. --Chtz (talk) 20:23, 29 September 2013 (UTC)

A standard calculator works in degrees and so sine(90°) is exactly 1, while when using radians sine(pi/2)=1 is correct. But this doesn't matter, it always describes how to invoke a function and get the result.--Dgbrt (talk) 10:38, 30 September 2013 (UTC)

However, I don't know any programming languages that use degree instead of radians by default. But that was indeed not my point: The point is that sine is an example of a function (independent of the programming paradigm used) and not a good example of functional programming. --Chtz (talk) 11:14, 30 September 2013 (UTC)

There is a difference between functional programming and using functions in imperative programming

@Dgbrt: I'm not reverting your last rewriting, since I'm fearing it will lead to an edit war. I don't doubt that you are a real programmer, but I somehow doubt that you have experience with functional programming (like e.g. Haskell, Lisp, ...). As I tried to explain, functions in functional programming don't have a state and therefore they don't have statements (especially no return statement). They simply describe functions in a mathematical sense, i.e. they have input parameters and result in a value. (They don't return that value, they just have that value). The if-else construct I was using was supposed to describe a case distinction, similar as a mathematician would describe the abs function: 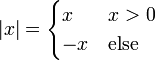$|x| = \begin{cases} x & x>0 \\ -x & \text{else}\end{cases}$.

Actually, a functional programmer would avoid such if-else constructs and write (for the non-tail-recursive variant)

 factorial 0 = 1
 factorial n = n * factorial (n-1)

And the interpreter/compiler will automatically find the most specialized case of the definition which can be matched to the input arguments: [1]

Here is a demonstration how a valid Haskell program with tail-recursion and the if-else construct would look like: [2] and this is how it (usually) would be written with pattern matching: [3] --Chtz (talk) 20:15, 29 September 2013 (UTC)

You're right, I am a real programmer. And so I try to explain the "recursive" issue to NON specialists. We should EXPLAIN but not ENHANCE the comic. My two cents...--Dgbrt (talk) 20:34, 29 September 2013 (UTC)

Ok, then the question remains if it is not more important to explain functional programming first? Currently, the second paragraph explains the difference between a function and a procedure in imperative programming and then mostly explains recursion for imperative programming (which I doubt will help understanding the comic -- how is it relevant if and where memory is allocated?). In the next paragraph I originally tried to describe how functional programming is different from imperative programming (after some editing there is not much left of it at the moment, it currently again describes more what imperative programming is). I assume there are more people who know recursion but have no idea of functional programming than the other way around. --Chtz (talk) 20:58, 29 September 2013 (UTC)

I'm not sure "which should not work because the return statement is missing" is relevent. In a given language, functions may only return values when a "return" is given (and immediately that one is given, ending all processing), otherwise giving "undefined", or "void" or the equivalent default state for an explicitly stated return-type. But in others they (in the absence of anything else, like an explicitly terminating "return" well within its own code) will use the bare evaluation of the very last statement within it as the return-value of that function/sub/procedure, if in tested at all by the calling-block (although it's prefereble to "return variable" at the end rather than just put "variable" as the last statement, for readability purposes, especially when it isn't "variable" but something that looks like (or is!) an evaulation/function call in its own right). The above being pseudocode (or "composite relatively common dialect code" not far off various common languages), surely the readability is the big concern, not the fact that (in certain languages, but not others) should not work. (Basically, have I just spent a paragaph saying "don't add that above statement, just put a 'return' into the pseudocode and everyone should be happy"? Yes. Yes, I believe I might have. Still.) 178.98.253.80 15:35, 30 September 2013 (UTC)

This [4] is a valid functional definition of the factorial function. There are no statements in pure functional programming, especially no return statements. (There are ways to simulate them, but that's beyond this conversation). If everyone thinks that we shall just explain recursion and tail-recursion and avoid talking about functional programming, go ahead and revert it back to before my first attempt to describe functional programming. I agree that functional programming can be hard to get at first, especially to programmers used to imperative programming, but I do think it is worth to know about it. If it is just the brace-less syntax that is confusing, we can use this [5] alternative (very uncommon in Haskell, but I agree that it's more important to make the code easy to understand). --Chtz (talk) 15:52, 30 September 2013 (UTC)

Lest I have made myself unclear (and you're replying to me), I'm happy with the code as is. The 'statement' I mentioned, above, was regarding the added explanatory text (not yours) not any code-statement. The other pseudocodes had "return"s in them, however, so for an argument of readability it might be useful to make that "prod" "return prod", although I (especially as a bit of a Perl fanatic) don't mind either way. I can deal with braces substituted by idents, in pseudocode, much as I can read either XML or YAML encoded data, fairly easily. ;) However, we've got quite a technical discussion going which (unlike code, even deliberately obfuscated Perl!) is not so easily untangled into who is replying to which bit and what they are trying to say (and why). Maybe we should switch to Lojban! 178.98.253.80 20:48, 30 September 2013 (UTC)

There is no agreement yet, if and when we should introduce/explain the concept of functional programming. At the moment the transition is very abrupt, partly because someone changed my first functional example to imperative code. The tail recursive example is at this very moment exactly the same as this valid functional code (written in Haskell). --Chtz (talk) 21:07, 30 September 2013 (UTC)

I agree, this is still chaos! Please explain "An imperative, recursive (but not tail-recursive) implementation can look like this:", I disagree and there is still no prove helping me or other people to understand. And beside: My first recursive program was to solve a one player game, written in Turbo Pascal in the middle of the eighties of the last century. And it was fast even at that time. --Dgbrt (talk) 21:47, 30 September 2013 (UTC)

I guess you mostly disagree on the non tail-recursiveness? Basically, this can be seen as the recursion can't be replaced by a simple replacement of the return statement with another function call, because after the call another operation (the multiplication by n) needs to be performed before the value can be returned. My original attempt on this article was to switch to functional programming at this point, since it does not make much sense to implement such a simple function recursively in an imperative language (admittedly, the transition to functional programming was way to abrupt). When implementing a function which searches inside a tree it often/usually makes sense to implement it recursively even in imperative languages and with some tricks you can also make this comparatively fast (I assume that was the point of your last two sentences?). To come back to 178.98... My intention was to structure the explanation approximately as follows:

1) Describe the difference between functional and imperative programming (assuming that most readers know what imperative programming is -- if we can't assume that, where shall we start?)

2) Give an example of a simple imperative function (e.g. the factorial function) written with typical imperative constructs (loops, assignments)

3) As this is not possible in functional programming introduce the concept of recursion and define the function recursively (this step was clearly to fast)

4) Explain the benefit of tail-recursion and give an tail-recursive example of factorial (also in functional programming)

5) Explain the actual joke!

6) Explain remaining parts (title text, ...) --Chtz (talk) 22:41, 30 September 2013 (UTC)

On your fourth point, the functional programming example is confusing, and strange. Why are you defining two seperate functions, when a single function would do? For example, an easy way to show this is:

 factorial[0] = 1
 factorial[n] = n * factorial(n - 1)

which, though not valid computer code, is valid mathematical syntax, and shows perfectly what a factorial function, in functional programming, does. The explanation would then be:

 factorial[6] = 6 * factorial[6-1] = 6 * 120 = 720
   factorial[5] = 5 * factorial[5-1] = 5 * 24 = 120
     factorial[4] = 4 * factorial[4-1] = 4 * 6 = 24
       factorial[3] = 3 * factorial[3-1] = 3 * 2 = 6
         factorial[2] = 2 * factorial[2-1] = 2 * 1 = 2
           factorial[1] = 1 * factorial[1-1] = 1 * 1 = 1
             factorial[0] = 1

or something similar to that. GBGamer117 (talk) 05:07, 2 October 2013 (UTC)

I would be totally fine (and originally intended) to have this definition at step 3). If you replace your [ ] brackets by ( ) parentheses, or leave them, it is actually valid Haskell code (and as you point out, [clear and intuitive as] valid mathematical syntax). The evaluation, however would rather go like:

 factorial(4) = 4 * factorial(3)
              = 4 * ( 3 * factorial (2)                 )
              = 4 * ( 3 * ( 2 * factorial (1)         ) )
              = 4 * ( 3 * ( 2 * ( 1 * factorial (0) ) ) )
              = 4 * ( 3 * ( 2 * ( 1 * 1 ) ) )
              = 4 * ( 3 * ( 2 * 1 ) ) = 4 * ( 3 * 2 ) = 4 * 6 = 24

That would actually give a nice example, why this recursion is less efficient than actual tail recursion: During evaluation, you need to build up an entire expression tree which you don't have to do for the tail-recursive way (it does not really matter for this simple function, though).

 factorial(4) = factorial_helper(4, 1) = factorial_helper(3, 4) = factorial_helper(2, 12) = factorial_helper(1, 24) = factorial_helper(0, 24) = 24

The number of numerical operations is actually the same (I omitted the steps of evaluating the products and differences), but you don't have to build up a large expression, before you can actually start multiplying. --Chtz (talk) 07:51, 2 October 2013 (UTC)

Tail Recursion?

Are we really certain "tail recursion" isn't also an innuendo for ongoing sexual relations? Tail is sometimes used as slang, and if it were received regularly, it would be tail recursion. 69.67.112.5 (talk) (please sign your comments with ~~~~)

Explain the concept, not the history?

I think that this page would benefit from simplifying the beginning to explain the concept without providing all of the background. Background can be applied later. I would suggest this:

Recursion is a common programming practice where a function calls itself. This can result in many layers of the function, all of which need to be kept track of until the program can get to the bottom layer. The last step of this process is to return the final value through all of the layers of function calls.

If there is nothing left for a function to do when the lower level returns, then there is no longer a need to keep track of the state of that layer. Instead of creating a new layer, a compiler that is smart enough can overwrite the existing layer with the new layer. This means that the new layer will pass its results directly to whatever initially called the function and not have to waste time passing the results up the stack of function calls. Making use of this optimization is called tail recursion, and it saves both time and memory requirements.

Functional programming is a programming language style that appeals to people who spend a lot of time staring at the notation used to describe higher math. This notation commonly uses recursion and formulas that include entire other formulas as variables in a higher level formula. Tail recursion was first introduced as a more efficient manner of handling recursion within functional programming languages, and they are currently the only programming languages that support this optimization.

Mythobeast (talk) 21:07, 3 March 2014 (UTC)

Frankly, I don't think the point here is about what concept it is. Tail recursion is just one of the many peculiar aspects of functional programming that, frankly, does not make that much different in the long run. (Frankly, a loop is about 20 times easier than tail recursion in about 90% of the cases; same for passing functions around). However, those things are rewarding to play with in and of themselves (and who care about the long run anyway? In the long term, we are all dead). At least that how I think of this slide. magice (talk)

Maybe the long explanation should be a trivia item?Kynde (talk) 21:59, 21 June 2014 (UTC)

I've read all of the explanation and all of the comments as of now. In all of it, I found no mention of explaining what the optimization itself consists of. In case it is one day decided to add that explanation, I want to add my 2 cents and explain it here, as readable to non-programmers as I can: "Computer programs are like cooking recipes: a ordered list of instructions. Usually, there are groups of instructions that are used regularly. To keep from copying and pasting these groups wherever they are needed, functions were created. When a computer executes a function, it jumps from the instruction it was executing to the first instruction of that function. When the function ends, the computer jumps back to the instruction that called the function (one after actually). Since functions can call other functions, the computer keeps a stack of function calls (and other things) to remember all the jumps it made. Think of it as a stack of heavy objects: usually, you can only move the topmost one. So, when the functions ends, the computer make the backward jumps in the reverse order they were stacked. A recursive function (explained above) may fill up the stack quickly. To avoid that, tail recursive functions (explained above) cause only the first function call to be stacked, no matter how many calls happen afterwards." Also, out of topic but, with these comments, I found out that the editing box have a limit on how much you can stretch it downwards. 108.162.219.148 18:58, 23 November 2014 (UTC)

I just reinstated a removed word, but it looks (unintentionally?) complicated as it is. It was one of two consecutive "that"s in a sentence with two other "that"s in, and perhaps not enough commas, semicolons, hyphens, emdashes and/or parentheses. I.e. "Another explanation is that the fact that that part of the title text is confusing is a metaphor for the fact that abstract mathematics and functional programming can be confusing" (then a clause-break comma and even more words...). Breaking it down "(the fact that) (that part)" is roughly "(an interpretation of) (a detail)". Or, to put it another way, that that "that" that that "that that" lost was necessary. But confusing. 172.70.85.177 06:25, 27 March 2022 (UTC)

I didn't quite get this until I started programming in OCaml for university - haha he's absolutely right. It's so satisfying. Beanie ^talk 12:11, 29 October 2024 (UTC)