Difference between revisions of "2117: Differentiation and Integration"
Sir Urquhart (talk | contribs) (Undo revision 289341 by 108.162.245.177 (talk)) |
Xurkitree10 (talk | contribs) m (→Transcript) |
||
| Line 84: | Line 84: | ||
==Transcript== | ==Transcript== | ||
| − | |||
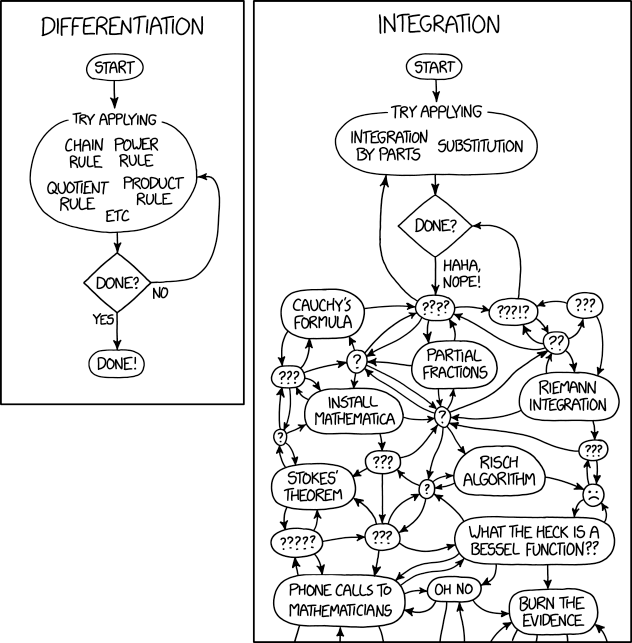
:[Two flow charts are shown.] | :[Two flow charts are shown.] | ||
Revision as of 11:30, 24 April 2023
Explanation
This comic illustrates the old saying "Differentiation is mechanics, integration is art." It does so by providing a flowchart purporting to show the process of differentiation, and another for integration.
Differentiation and Integration are two major components of calculus. As many Calculus 2 students are painfully aware, integration is much more complicated than the differentiation it undoes.
However, Randall dramatically overstates this point here. After the first step of integration, Randall assumes that any integration can not be solved so simply, and then dives into a step named "????", suggesting that it is unknowable how to proceed. The rest of the flowchart is (we can assume deliberately) even harder to follow, and does not reach a conclusion. This is in contrast to the simple, straightforward flowchart for differentiation. The fact that the arrows in the bottom of the integration part leads to nowhere indicates that "Phone calls to mathematicians", "Oh no" and "Burn the evidence" are not final steps in the difficult journey. The flowchart could be extended by Randall to God-knows-where extents.
It should be noted that Randall slightly undermines his point by providing four different methods, and an "etc", and a "No"-branch for attempting differentiation with no guidelines for selecting between them.
Differentiation
For any 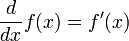 and
and 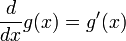 , it follows that
, it follows that 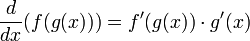 .
.
For any 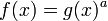 and
and 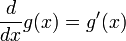 , it follows that
, it follows that 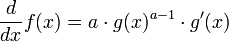 .
.
For any 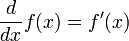 and
and 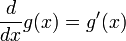 , it follows that
, it follows that 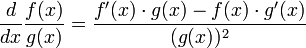 if
if 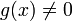 .
.
For any 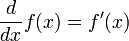 and
and 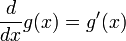 , it follows that
, it follows that 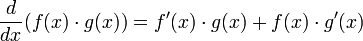 .
.
Integration
The "product rule" run backwards. Since 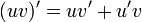 , it follows that by integrating both sides you get
, it follows that by integrating both sides you get 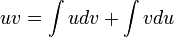 , which is more commonly written as
, which is more commonly written as 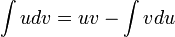 . By finding appropriate values for functions
. By finding appropriate values for functions 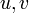 such that your problem is in the form
such that your problem is in the form 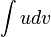 , your problem may be simplified. The catch is, there exists no algorithm for determining what functions they might possibly be, so this approach quickly devolves into a guessing game - this has been the topic of an earlier comic, 1201: Integration by Parts.
, your problem may be simplified. The catch is, there exists no algorithm for determining what functions they might possibly be, so this approach quickly devolves into a guessing game - this has been the topic of an earlier comic, 1201: Integration by Parts.
The "chain rule" run backwards. Since 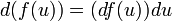 , it follows that
, it follows that 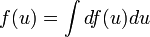 . By finding appropriate values for functions
. By finding appropriate values for functions 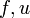 such that your problem is in the form
such that your problem is in the form 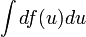 your problem may be simplified.
your problem may be simplified.
Cauchy's Integral formula is a result in complex analysis that relates the value of a contour integral in the complex plane to properties of the singularities in the interior of the contour. 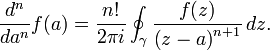 It is often used to compute integrals on the real line by extending the path of the integral from the real line into the complex plane to apply the formula, then proving that the integral from the parts of the contour not on the real line has value zero.
It is often used to compute integrals on the real line by extending the path of the integral from the real line into the complex plane to apply the formula, then proving that the integral from the parts of the contour not on the real line has value zero.
Partial fractions is a technique for breaking up a function that comprises one polynomial divided by another into a sum of functions comprising constants over the factors of the original denominator, which can easily be integrated into logarithms.
Install Mathematica
Mathematica is a modern technical computing system spanning most areas. One of its features is to compute mathematical functions. This step in the flowchart is to install and use Mathematica to do the integration for you. Here is a description about the intricacies of integration and how Mathematica handles those. (It would be quicker to try Wolfram Alpha instead of installing Mathematica, which uses the same backend for mathematical calculations.)
The Riemann integral is a definition of definite integration. 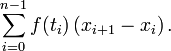 Elementary textbooks on calculus sometimes present finding a definite integral as a process of approximating an area by strips of equal width and then taking the limit as the strips become narrower. Riemann integration removes the requirement that the strips have equal width, and so is a more flexible definition. However there are still many functions for which the Riemann integral doesn't converge, and consideration of these functions leads to the Lebesgue integral. Riemann integration is not a method of calculus appropriate for finding the anti-derivative of an elementary function.
Elementary textbooks on calculus sometimes present finding a definite integral as a process of approximating an area by strips of equal width and then taking the limit as the strips become narrower. Riemann integration removes the requirement that the strips have equal width, and so is a more flexible definition. However there are still many functions for which the Riemann integral doesn't converge, and consideration of these functions leads to the Lebesgue integral. Riemann integration is not a method of calculus appropriate for finding the anti-derivative of an elementary function.
Stokes' theorem is a statement about the integration of differential forms on manifolds. 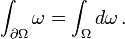 It is invoked in science and engineering during control volume analysis (that is, to track the rate of change of a quantity within a control volume, it suffices to track the fluxes in and out of the control volume boundary), but is rarely used directly (and even when it is used directly, the functions that are most frequently used in science and engineering are well-behaved, like sinusoids and polynomials).
It is invoked in science and engineering during control volume analysis (that is, to track the rate of change of a quantity within a control volume, it suffices to track the fluxes in and out of the control volume boundary), but is rarely used directly (and even when it is used directly, the functions that are most frequently used in science and engineering are well-behaved, like sinusoids and polynomials).
The Risch algorithm is a notoriously complex procedure that, given a certain class of symbolic integrand, either finds a symbolic integral or proves that no elementary integral exists. (Technically it is only a semi-algorithm, and cannot produce an answer unless it can determine if a certain symbolic expression is equal to 0 or not.) Many computer algebra systems have chosen to implement only the simpler Risch-Norman algorithm, which does not come with the same guarantee. A series of extensions to the Risch algorithm extend the class of allowable functions to include (at least) the error function and the logarithmic integral. A human would have to be pretty desperate to attempt this (presumably) by hand.
Bessel functions are the solution to the differential equation 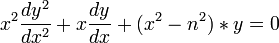 , where n is the order of Bessel function. Though they do show up in some engineering, physics, and abstract mathematics, in lower levels of calculus they are often a sign that the integration was not set up properly before someone put them into a symbolic algebra solver.
, where n is the order of Bessel function. Though they do show up in some engineering, physics, and abstract mathematics, in lower levels of calculus they are often a sign that the integration was not set up properly before someone put them into a symbolic algebra solver.
Phone calls to mathematicians
This step would indicate that the flowchart user, desperate from failed attempts to solve the problem, contacts some more skilled mathematicians by phone, and presumably asks them for help. The connected steps of "Oh no", "What the heck is a Bessel function?" and "Burn the evidence" may suggest the possibility that this interaction might not play out very well and could even get the caller in trouble. Specialists and renowned experts being bothered - not to their amusement - by strangers, often at highly inconvenient times or locations, is a common comedic trope, also previously utilized by xkcd (for example in 163: Donald Knuth).
Burn the evidence
This phrase parodies a common trope in detective fiction, where characters burn notes, receipts, passports, etc. to maintain secrecy. This may refer to the burning of one's work to avoid the shame of being associated with such a badly failed attempt to solve the given integration problem. Alternatively, it could be an ironic hint to the fact that in order to find the integral, it may even be necessary to break the law or upset higher powers, so that the negative consequences of a persecution can only be avoided by destroying the evidence.
Symbolic integration is the basic process of finding an antiderivative function (defined with symbols), as opposed to numerically integrating a function. The title text is a pun that defines the term not as integration that works with symbols, but rather as integration as a symbolic act, as if it were a component of a ritual. A symbolic act in a ritual is an act meant to evoke something else, such as burning a wooden figurine of a person to represent one’s hatred of that person. Alternatively, the reference could be seen as a joke that integration might as well be a symbol, like in a novel, because Randall can't get any meaningful results from his analysis.
Transcript
- [Two flow charts are shown.]
- [The first flow chart has four steps in simple order, one with multiple recommendations.]
- DIFFERENTIATION
- Start
- Try applying
- Chain Rule
- Power Rule
- Quotient Rule
- Product Rule
- Etc.
- Done?
- No [Arrow returns to "Try applying" step.]
- Yes
- Done!
[The second flow chart begins like the first, then descends into chaos.]
- INTEGRATION
- Start
- Try applying
- Integration by Parts
- Substitution
- Done?
- Haha, Nope!
- [Chaos, Roughly from left to right, top to bottom, direction arrows not included.]
- Cauchy's Formula
- ????
- ???!?
- ???
- ???
- ?
- Partial Fractions
- ??
- ?
- Install Mathematica
- ?
- Riemann Integration
- Stokes' Theorem
- ???
- ?
- Risch Algorithm
- ???
- [Sad face.]
- ?????
- ???
- What the heck is a Bessel Function??
- Phone calls to mathematicians
- Oh No
- Burn the Evidence
- [More arrows pointing out of the image to suggest more steps.]
Discussion
Darn, I have no idea what this comic is about. Randal has eluded my yet again. Linker (talk) 17:43, 27 February 2019 (UTC)
- Calculus. 162.158.79.143 18:16, 27 February 2019 (UTC)
And Calc 2 is why I stopped being a Computer Science major and moved (eventually) to majoring in English. Consistent 4.0s in math through Trig and Calc I ... 1.6 in Calc II, retook and got a 1.8. Without the Calc, couldn't do the physics; without the physics, couldn't get my 2-yr degree and move on from community college to a full university. I don't know what all the integration stuff in the flowchart is (since I didn't do well in Calc and it was a long time ago), but there's so very many things that become nonelementary integrals that all sorts of special tricks have to be employed for things that look like they should be easy. It's like having a problem that's very easy to do division on, but requires special advanced mathematical tricks to use multiplication upon.108.162.216.208 19:07, 27 February 2019 (UTC)
Going to start learning integration in 3 weeks... Wish me luck. 162.158.62.96 12:53, 3 November 2021 (UTC)
Basic ideas: Integration by parts is the reverse of the Product Rule. Substitution is the reverse of the Chain Rule. Cauchy's Formula gives the result of a contour integration in the complex plane, using "singularities" of the integrand. Partial fractions is just splitting up one complex fraction into a sum of simple fractions, which is relevant because they are easier to integrate. Stokes theorem is the relationship between an integral over an area, and an integral over the boundary of said area. Riemann integration was the first rigorous definition of integration. This has been superseded by Lesbesgue integration. Bessel functions are like 2d versions of sin and cos, and turn up sometimes when doing integration.162.158.89.61 20:14, 27 February 2019 (UTC)
- "Lesbesgue integration." Best. Freudian. Slip. Ever. SCNR :P 162.158.91.59 08:28, 28 February 2019 (UTC)
I know what you mean ;). After all, Gen 8 Pokemon was announced the other day, so you read it as "Pokemon League Integration". Completely understandable. 172.68.78.28 14:40, 28 February 2019 (UTC) Shouldn't Wolfram Alpha be somewhere in that flowchart? 162.158.255.142 20:54, 27 February 2019 (UTC)
Glad to see I'm not the only one who is too dumb to integrate 162.158.90.36 21:02, 27 February 2019 (UTC)
- Symbolic differentiation is just going through algorithm ; there are few functions which don't have it but they tend to be constructed in complicated way, and if function have differentiation it's usually easy to find it. Symbolic integration requires lot of thinking and trial and error ; even very easy function may lack primitive function and even if they don't, you may be unable to find it except randomly. If it's exercise in book, the ones for differentiation are done by thinking about some interesting function and putting it there. The ones for integration are done by thinking about some interesting function and putting it's differentiation there. -- Hkmaly (talk) 23:38, 27 February 2019 (UTC)
Oddly enough it mentions Riemann integration, but that is the integral most people know how to use. Turns out there are a lot more (e.g. lebesgue and generalized riemann integrals). I'm halfway through a second semester of real analysis and was floored by how involved integration can be. 172.68.34.106 21:36, 27 February 2019 (UTC)
One of my professors once said: "Never try to integrate a function. Almost all (in a strict mathematical sense) functions are impossible to integrate, so there is no reason why you should even try." --162.158.88.128 07:52, 28 February 2019 (UTC)
How is there no "+ C" joke in there Blagae (talk) 13:16, 28 February 2019 (UTC)
Probably because he put a +C joke in 1201:_Integration_by_Parts. 108.162.219.160 13:48, 2 March 2019 (UTC)
Why is all the maths broken GcGYSF(asterisk)P(vertical line)e (talk) 22:24, 4 May 2022 (UTC)
Risch algorithm
I thought I could contribute to the article with a better explanation of the Risch algorithm, since I have a bit of expertise here -- I've read all the original papers, plus the Cherry papers that add the extra features like Li and erf. I pulled out some of the old papers to review my knowledge of symbolic differential algebra (it's been a while!) then typed up a careful explanation which corrected some errors in the original description and fleshed out many more details... possibly excessively, but hey, that's kind of our calling here.
Then I saw that Glassvein completely removed my version for what appears to be the original without so much as a mention in the edit description. What gives? I
CRGreathouse (talk) 04:59, 28 February 2019 (UTC)
- Probably due to simultaneous editing. I've restored your definition. 162.158.88.128 16:52, 28 February 2019 (UTC)
- OK, wasn't sure if it was intentional (if somehow it was worse). Thanks! CRGreathouse (talk) 01:34, 1 March 2019 (UTC)
That was indeed an accident due to simultaneous editing. My bad! Glassvein (talk) 02:47, 5 March 2019 (UTC)
Numerical Integration
Better still...plot the graph - cut along the line - weigh the part under the line. :-) SteveBaker (talk) 20:46, 28 February 2019 (UTC)
[Anonymous: I understand mathematically that integration is much more difficult than differentiation, but is there a possibility that Randall is making the comment that the same is true for Society? Integration has proved very difficult, and has led to riots, but experience shows that dividing our society up into small subgroups (that then argue with each other, but don't spend enough time together for riots) is relatively easy.] 108.162.219.112 (talk) (please sign your comments with ~~~~)
- Good luck plotting Weierstrass function. -- Hkmaly (talk) 00:05, 9 March 2019 (UTC)
overstates the case?
Current summary says that the comic overstates the case of how difficult integration can be. I'm not sure that's true. Sure, you can use numerical integration to get a specific area under the curve, but that's not what the comic is referring to. Unless some mathematician can show here how integration can be done by repeatedly following a set of fixed rules, Ithis comic is actually completely accurate. And that's why it's funny. :-)
Purify the Power rule?
The derivative power rule shown is combined with the chain rule. I think it should be stated to be a pure power rule, without the chain rule components. When I tried making that adjustment, I got error messages that I could not resolve, so could someone who knows how the MATH feature works remove the chain rule from the power rule? Nutster (talk) 18:44, 26 December 2021 (UTC)
Change to explanation of substitution
So the LaTeX on this wiki is apparently broken, meaning we can't change the math things without stuff screwing up. Unfortunately, there are a lot of alterations I'd like to make. Most are minor, like simplifying the power rule explanation, but more importantly, the explanation for integration by substitution is straight-up wrong. I'm going ahead with the change anyway, because hey, a broken explanation can't be any worse than a wrong explanation, right? I'm just gonna wait and hope that this gets fixed in the future. ISaveXKCDpapers (talk) 14:39, 11 June 2024 (UTC)
Issues with Math display
I'm not a CS student... but I do software engineering and web servers including MediaWiki. The issue is described here: Missing texvc executable error
I will note that the installed version of Math per the Special:Version page is 7 years old... Yikes. EricM (talk) 03:41, 31 July 2024 (UTC)
- It's from this point that the math-markup went wrong (it was corrected, factually, but using unsupported markup). I don't have enough experience with MathML to know why the Substitution rewrite fails and becomes redtext whilst the Cauchy markup (and others) does not, with substantially the same invoked formatting. Is it just an unbalanced paren or incorrect delimiter..? Visually, seems not, but the failover text seems to refer to errors in the layers of parsing module(s) beyond the edited source and thus not as explanatory or demonstrably obvious as to where the mishandling gets invoked.
- From a purely eyeballed parsing, the markup grammar looks consistent, though. I mean, the difference between the
<math>being immediately followed by the apparently more usual algebra of having a whitespace between it and the algebra seemed to be a possibility (an easy work-around, one perhaps imagining that the current library has a slight regex error when looking for initial components), but that doesn't really match the pattern of what does and doesn't (apparently) work. - So let's look at three things that don't and do render...
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): d(f(u)) = f'(u) \frac{du}{dx} dx
note: is mathtag-space-algebra, still does not work
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): f(u) = \int f'(u) \frac{du}{dx} dx
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \int f'(u) \frac{du}{dx} dx
- ...and compare with one (more complicated) bit that clearly does work...
- Try sub-elements, first testing \frac usage
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{du}{dx}
fails
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{x}{y}
fails (so not du or dx at fault
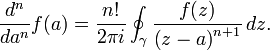 works (as we know, taken from Cauchy)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{d^n}{da^n}f(a) = \frac{n!}{2\pi i} \oint_\gamma \frac{f(z)}{\left(z-a\right)^{n+1}}\, dz
does not work (just an ending dot removed)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{du}{dx}.
fails (dot added to barebones, so it's not that)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): d(f(u)) = f'(u) \frac{du}{dx} dx.
fails (dot added to full version)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{d^n}{da^n}f(a) = \frac{n!}{2\pi i} \oint_\gamma \frac{f(z)}{\left(z-a\right)^{n+1}}.
does not work (just a trailing ending term removed)
works (as we know, taken from Cauchy)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{d^n}{da^n}f(a) = \frac{n!}{2\pi i} \oint_\gamma \frac{f(z)}{\left(z-a\right)^{n+1}}\, dz
does not work (just an ending dot removed)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{du}{dx}.
fails (dot added to barebones, so it's not that)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): d(f(u)) = f'(u) \frac{du}{dx} dx.
fails (dot added to full version)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{d^n}{da^n}f(a) = \frac{n!}{2\pi i} \oint_\gamma \frac{f(z)}{\left(z-a\right)^{n+1}}.
does not work (just a trailing ending term removed)
- ...you know, this set of results (described as failed or working as I currently see them, in case this changes in the future) leads me to just one particular conclusion. The working Cauchy formula is cached from when the "TEX validator and converter" worked (and piped through the postcript/whatever rendered), meaning that this formula image isn't broken because it's remembered from when it was Ok.
- Anything new we try, however, finds no cached result and fails because of an actual (failed) later update of the texvc. (Conceivably, the >7yo version of Math would be happily working, even today.) Note that there are many comments that Latex (if we use that) can be finicky, and getting ImageMagick binaries manually compiled properly (if that's the chosen renderer) has been known to be very difficult.
- One could say that it's more that it was actively broken, rather than fell into unupdayed obselesence. Yes, by not updating something, there may be further dependancies that later get invoked that fail/complain about the older element (perhaps for good reasons, or perhaps just for "I'm not going to test my product against anything older than <version X>, so I'll just make it failover to make it the end-user's problem") and stagnating software isn't exactly best practice, but I see no obvious signs that the vital (half-)updated library was actually necessary to patch anything as severe as a security exploit, probably just version-tweak that the lack of probably shouldn't have mattered too much unless a specific new feature (not being used here) was desired.
- But then, I'm personally running software and OSes a full quarter of a century old (knowing how much 'risk' I'm taking... practically zero, given that it's not networked up) on hardware that's slightly older, plus have some of the very latest systems that have totally annoying new behaviours (how on earth can you make Notepad more difficult to use..? ...and my muscle-memory is now nearly useless when trying to use Win11's folder windows with long-used keyboard shortcuts that have worked pretty much since Windows3.0!), so perhaps I'm naturally more ambivalent against just updating everything at all times (never mind anything like CrowdStrike, which I thankfully dodged being affected by).
- So, anyway, yes something (system-deep) needs updating properly. Or else get another system to render what we want and then upload that image to use here as an inline image. If I actually had an upload-enabled account then that's what I'd try myself, next. Or perhaps the solution (this side of the necessary server-priviliges) is access an existing version as a cross-server transcluded resource. 172.69.43.166 09:54, 31 July 2024 (UTC)
- Agree with the above; it's likely that an unrelated update (OS/wiki) created the incompatibility. However, the status quo is also undesirable. If the cache were ever to be purged, all math expressions throughout the wiki would be broken. Failing to update is just going to push things toward abyss... EricM (talk) 00:48, 2 August 2024 (UTC)