Difference between revisions of "Talk:2028: Complex Numbers"
(half the operations gets you half a group.) |
|||
| Line 19: | Line 19: | ||
Shouldn't the description of a group involve ''two'' operations? There is a binary operation that gloms two things together to make a new thing, but there's also a unary operation that takes only one thing and makes a new thing -- the inverse. Without the unary operation, you only have a {{w|semigroup}}.[[Special:Contributions/108.162.215.160|108.162.215.160]] 09:40, 5 August 2018 (UTC) | Shouldn't the description of a group involve ''two'' operations? There is a binary operation that gloms two things together to make a new thing, but there's also a unary operation that takes only one thing and makes a new thing -- the inverse. Without the unary operation, you only have a {{w|semigroup}}.[[Special:Contributions/108.162.215.160|108.162.215.160]] 09:40, 5 August 2018 (UTC) | ||
| + | : No. The inverse operation arises as a consequence of the fact that it's a group. A group satisfies four conditions: 1. it is closed under the operation, 2. the operation is associative 3. there is an identity e such that a op e = e op a = a. 4. For every element a, there is a unique element b such that a op b = b op a = e. The inverse function falls out as a result of conditions 3 and 4 [[User:Jeremyp|Jeremyp]] ([[User talk:Jeremyp|talk]]) 10:26, 6 August 2018 (UTC) | ||
Revision as of 10:26, 6 August 2018
I assume this is strictly a coincidence, but in reference to the title-text, I'll just mention that Caucher Birkar [the mathematician whose Fields Medal was stolen minutes after he received it in Rio de Janeiro on Weds (1Aug2018)] received the award for work in algebraic geometry. Arcanechili (talk) 16:34, 3 August 2018 (UTC)
- Perhaps it's causal not coincidental. Medal theives and perhaps Randall might read the news also. [[1]] 162.158.79.209 00:34, 4 August 2018 (UTC)
I've added a basic description of Abelian groups in the title text, and that's about as much as I know about such topics. I'm not sure what a "meta-Abelian group" is, is that an Abelian group of other groups? Also, could someone add basic descriptions of algebreic geometry and geometrical algebra? 172.68.94.40 18:42, 3 August 2018 (UTC)
In the title text, since groups are a concept within mathematics, it seems odd to consider mathematics as a whole forming any sort of group within itself, which I suspect is the first part of the pun. Secondly, since groups involve the commutative property, I think the last part is a pun about the order of the words algebra and geometry, as if they're commutative themselves! Ianrbibtitlht (talk) 19:19, 3 August 2018 (UTC)
- I meant to say 'abelian' groups involve the commutative property, and the meta prefix is referring to the fact that it's about the names rather than the mathematical details - i.e. commutative in metadata only. Ianrbibtitlht (talk) 19:24, 3 August 2018 (UTC)
- I guess the joke is that informally mathematicians form a group (a number of people classed together), what would strictly be a set in mathematics. While in mathematics, a group is an algebraic structure consisting of a set of elements equipped with an operation that combines any two elements to form a third element and that satisfies specific conditions. --JakubNarebski (talk) 21:18, 3 August 2018 (UTC)
It's a false dilemma. Complex numbers are vectors (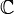 is a two-dimensional
is a two-dimensional 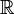 -vector space, and more generally every field is a vector space over any subfield), but that doesn't change anything about the fact that
-vector space, and more generally every field is a vector space over any subfield), but that doesn't change anything about the fact that 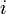 is by definition a square root of -1. Zmatt (talk) 20:38, 3 August 2018 (UTC)
is by definition a square root of -1. Zmatt (talk) 20:38, 3 August 2018 (UTC)
Fun factoid: not only is 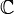 the unique proper field extension of finite degree over
the unique proper field extension of finite degree over 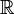 (since
(since 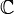 is algebraically closed), but the converse is true as well:
is algebraically closed), but the converse is true as well: 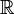 is the only proper subfield of finite index in
is the only proper subfield of finite index in 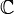 . They're like a weird married couple. Zmatt (talk) 20:53, 3 August 2018 (UTC)
. They're like a weird married couple. Zmatt (talk) 20:53, 3 August 2018 (UTC)
Altho there are no "meta-abelian" groups there are metabelian groups. If xy=yx then the commutator [x,y]=xyx^{-1}y^{-1}=1. The group generated by the commutators -- the commutator subgroup -- is thus a measure of how far a group is from being abelian. A metabelian group is a nonabelian group whose commutator subgroup is abelian. Thus a metabelian group is one made of a stack of two abelian groups. It is "meta-abelian" in that sense. A standard example is the group of invertible upper-trianglular matrices. The commutators all have 1s on the diagonals.
- One should note that the concept of complex numbers actually is older than vector spaces. So while it is true that complex numbers are a cool variant of vectors, historically that's not true, because vectors were more or less unknown when complex numbers were used for the first time. --162.158.90.6 09:59, 4 August 2018 (UTC)
Shouldn't the description of a group involve two operations? There is a binary operation that gloms two things together to make a new thing, but there's also a unary operation that takes only one thing and makes a new thing -- the inverse. Without the unary operation, you only have a semigroup.108.162.215.160 09:40, 5 August 2018 (UTC)
- No. The inverse operation arises as a consequence of the fact that it's a group. A group satisfies four conditions: 1. it is closed under the operation, 2. the operation is associative 3. there is an identity e such that a op e = e op a = a. 4. For every element a, there is a unique element b such that a op b = b op a = e. The inverse function falls out as a result of conditions 3 and 4 Jeremyp (talk) 10:26, 6 August 2018 (UTC)
