Difference between revisions of "2091: Million, Billion, Trillion"
m (→Explanation) |
(→Transcript) |
||
| Line 23: | Line 23: | ||
==Transcript== | ==Transcript== | ||
{{incomplete transcript|Do NOT delete this tag too soon.}} | {{incomplete transcript|Do NOT delete this tag too soon.}} | ||
| + | |||
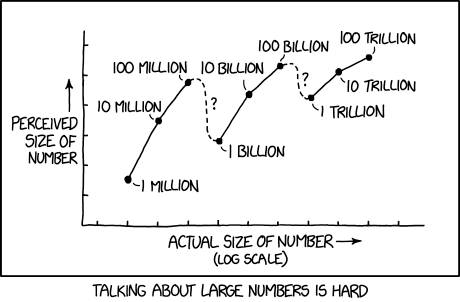
| + | :[A graph with Y-axis labeled "Perceived size of number" and X-axis labeled "Actual size of number (log scale)".] | ||
| + | :[The graph shows points that are labeled with numbers from "1 million" to "100 trillion". The perceived size increases otherwise, but decreases between 100 million and 1 billion, and between 100 billion and 1 trillion. The decreases are shown as dashed lines labeled "?". The increases and decreases in perceived size become smaller as the numbers grow in actual size.] | ||
{{comic discussion}} | {{comic discussion}} | ||
Revision as of 14:39, 28 December 2018
| Million, Billion, Trillion |
 Title text: You can tell most people don’t really assign an absolute meaning to these numbers because in some places and time periods, “billion” has meant 1,000x what it's meant in others, and a lot of us never even noticed. |
Explanation
| This is one of 72 incomplete explanations: This needs about a thousand years of rewriting, and I assume we'll want to do a chart of X and Y positions as with most chart comics. Do NOT delete this tag too soon. If you can fix this issue, edit the page! |
Much like comic 558, this comic addresses the difficulty ordinary people have with large numbers. Though most if not all people intuitively understand the difference between one object and two objects, or one object and ten objects, or even one object and a hundred objects, as numbers increase most people's ability to innately conceive of the numbers being discussed decreases remarkably quickly. When numbers reach the millions and the billions, and especially the trillions, most people don't truly process the numbers at all, and instead conceive of them as some version of a drastically-oversimplified concept such as "very big." Where comparing one to ten is simple, comparing "very big" to a different "very big" can prove extremely challenging, and will certainly require non-intuitive, conscious thinking.
The comic represents this challenge by providing a graph which represents Randall's intuitive conception of the values of various very large numbers, and said conception's misalignment with reality. Though some trends reflect the real value of the numbers on the graph, i.e. 100 million larger than 10 million larger than 1 million and 1 billion larger than 1 million, the curve is far from the linear (exponential on the log-scaled axes) path it should take, with 1 billion being intuitively understood as less than 100 million, based, presumably, on the fact, easily comprehended on an intuitive level, that 100 is larger than 1, and therefore the presence of 100 in 100 million places it at a higher value than the 1 in 1 billion would place the latter. In reality, of course, 1 billion is ten times larger than 100 million, but the comic deals not with actual reality, but with the perception of reality of these numbers before conscious thought is applied.
The most interesting parts of the graph, and the parts where the disconnect between intuition and reality becomes clearest, are the dashed sections labeled with question marks, the one between 100 million and 1 billion, the other between 100 billion and 1 trillion. Here two competing intuitive understandings compete for dominance. On the one hand, the intuitive understanding described above, with 100 trumping 1, would see the curve taking a sharp downturn. On the other hand, the path from 100 million to 1 billion is paved with such numbers as 500 million, 700 million, and 900 million, all of which would theoretically be seen intuitively as larger than 100 million, thanks to the fact that 9 is greater than 7, and 7 greater than 5, and so on, bending the curve up rather than down. These two conflicting intuitions leave Randall with no single intuitive path for the two dashed sections, leading to their dashed and questioned state.
The comic's caption and title highlight another problem surrounding the intuitive grasping of large numbers: the flaws in the English words used for them. For instance, nothing about the word "million" suggests smallness relative to the word "billion" on an intuitive scale. This unintuitive language contributes greatly to the "100 trumps 1" intuitive fallacy described above.
The title text references a classic, and highly relevant, example of a disconnect between British and American English. For all English speakers, 1 million constitutes 1,000 thousands, or, said less ambiguously, 10^6. However, the definition of billion varies depending which side of the Atlantic Ocean you happen to land on. In America, 1 billion equals 1,000 millions, or 1000*10^6=10^9. In Britain, 1 billion equals 1 million millions, or 10^6*10^6=10^12, with the base unit changing when you have a unit's worth multiple of the unit (for those immediately asking "what did they call a thousand million, then?", the answer is "well, naturally, a thousand million", though there is also the archiac "milliard"). In other words, 1 billion objects in England would register as 1,000 billion objects to an American, despite the fact that the number of objects has remained the same. Though people in Britain often use the American definition as of the past few decades, the fact that such a staggering difference of terminology was able to remain, and be almost completely unknown, perfectly highlights Randall's point about the failure of human intuition, and English terminology, in the discussion of extremely large numbers.
Also in some European languages (like French, German and the Scandinavian countries) the word milliard (meaning 1,000 million) still exists in some way (e.g. milliard in French, Milliarde in German, milliard in Danish, milliárd in Hungarian, etc.) and is used normally, and is different from the word billion which is a 1,000 milliard (or 1,000,000 million). These languages unlike English never used the short scale, so a billion never meant 1,000 million in them. This difference to the US numbering scheme often causes confusion when translating articles with large numbers in them, as translators sometimes forget to change the scheme from short to long, and wrongfully translate billion to billion instead to milliard which will make the number actually 1,000 times larger in the translation.
Transcript
| This is one of 44 incomplete transcripts: Do NOT delete this tag too soon. If you can fix this issue, edit the page! |
- [A graph with Y-axis labeled "Perceived size of number" and X-axis labeled "Actual size of number (log scale)".]
- [The graph shows points that are labeled with numbers from "1 million" to "100 trillion". The perceived size increases otherwise, but decreases between 100 million and 1 billion, and between 100 billion and 1 trillion. The decreases are shown as dashed lines labeled "?". The increases and decreases in perceived size become smaller as the numbers grow in actual size.]
Discussion
I actually think we have too many names for large numbers. It's really only necessary to introduce a new name when you reach the square of the previous name. So, we'd still have tens and hundreds, but there's no need for "one thousand, one hundred" when you can just have "eleven hundred". We'd be better off just naming 10^4, 10^8, 10^16, 10^32, and that's already well beyond anything needed for normal usage, with only a handful of names. None of this "quattuordecillion" stuff that no-one can remember without sitting down and working it out. 172.68.86.64 05:32, 28 December 2018 (UTC)
- And what you get is a super-weird "double-log" scale! The British (and other nations') usage is correct. Anything above thousand is completely abstract for a human being and intuitively nonlinear (some nations - ancient Greeks and others - go as far as ten thousands, a myriad, but this is it). A thousand squared is already far beyond intuition so it is a good candidate for a new unit representing A BIG NUMBER, plus log scale is a good abstraction allowing for rapid expansion in magnitude. So taking Latin numerals and adding an -illion suffix (except the irregular million) for subsequent powers of 10^6 is a really convenient system. Of course, it goes only as far as ordinary Latin numbers go, then you need to invent something else, but at this point it's only for entertainment. For anything physical you probably would never need a number much larger than a googol. -- 162.158.90.90 09:26, 28 December 2018 (UTC)
- I think we should refrain from saying one usage is correct over the other - that's just arrogant and mean. That said, the current explanation states that usage is different between American and British English, but my reading on Wikipedia (which is already hyperlinked in the explanation) states that in recent decades Britain has declared their use of short units and therefore British English is now the same as American English. The only regions where it appears there is still usage of the long system is in French and Spanish speaking regions, as well as some special cases around the world. Don't shoot the messenger - I'm just repeating what it states on the Wikipedia page. Ianrbibtitlht (talk) 10:15, 28 December 2018 (UTC)
- Rereading the Wikipedia page, it was in 1974 that Britain declared their use of the short scale for large numbers. Ianrbibtitlht (talk) 10:19, 28 December 2018 (UTC)
- Actually, Germany also uses the "long" (i.e. natural) scale to this day, and I remember how much trouble I had understanding the American system. As the second comment above states, the long scale is (prefix)-llion = 10^(prefix*6), or (prefix)-lliarde = 10^(prefix*6+3); whereas in the short system, (prefix)-llion = 10^(prefix*3+3), which is rather less obvious, if you have any intuition for numbers (and a little Latin). German Wikipedia tells me that the long scale was invented 1484/1550 by French mathematicians, and the short one in the 17th century in Italy and France by some geniuses that thought when grouping the digits on paper by three instead of six, they should change the group names to make confusion complete. Also, they claim official usage of the short variant is in USA, Brazil, and English-language finance. The names for the systems, however, are from 1975, from yet another French mathematichan, Geneviève Guitel. --Khms (talk) 10:59, 28 December 2018 (UTC)
- East Asian languages such as Japanese actually do use the power-4 scale, with the naming being ten, ten x ten = hundred, hundred x hundred = big'ousand, big'ousand x big'ousand = morebiggienoughty, morebiggienoughty x morebiggienoughty = superbiggienoughty, etc.
- Not quite--at least not nowadays. There's a word for "ten-thousand ('man' in Japanese)", so a million is "100 ten-thousands", a 10 million is "1000 ten-thousands", and 100 million goes to the new word "1 hundred-million ('oku' in Japanese)" The scale goes by 10^4, with a new word for 10^8, 10^12, 10^16, etc. though most people won't encounter anything much higher than that. Correspondingly, old Japanese text would put the commas every 4 digits. Modern practice is to put the comma every 3 digits to match Western practice, which actually makes it harder to read in Japanese. 172.68.141.148 20:49, 2 January 2019 (UTC)
- The "named power-of-two power-of-ten" system you propose already exists, in the form of Donald Knuth's -yllion system. 10^2 = hundred, 10^4 = myriad, 10^8 = myllion, 10^16 = byllion, 10^32 = tryllion, etc. 10^63 would be written as "ten hundred myriad myllion byllion tryllion", and the next power of 10, 10^64, is one quadryllion. 10^100 (i.e. googol) is one myriad tryllion quadryllion. It's quite efficient, as you point out, and were I to rewrite our number system from scratch, it's the system I would use. Unfortunately, nobody alive grew up with -yllions, so we're stuck with the inefficiency of named multiple-of-three powers-of-ten. Although apparently some parts of East Asia at some points in time used a similar system, with specific characters for the -yllions up to 10^4096. I find myself severely disappointed that those characters are now used to represent different (and much smaller) numbers. --Someone Else 37 (talk) 01:38, 30 December 2018 (UTC)
I said this earlier, and I'm going to say it again - the split between use of the short scale and the long scale is NOT a U.S. thing, nor an Atlantic Ocean thing! Just navigate to the hyperlinked page on Wikipedia, and scroll down to the graphic map showing who uses which system to see this very clearly. The majority of the globe uses the short scale except for the following regions: Europe other than Britain, Iran, some countries in Africa, and some countries in Latin America and South America, as well as French speaking regions in otherwise short-scale countries. Notable non-U.S. short-scale countries include Russia and Australia, along with Eastern South America and most of Africa. It's frustrating when people insist on making something about those U.S.A. people that has nothing to do with us. Ianrbibtitlht (talk) 14:51, 28 December 2018 (UTC)
- While you are right that these passages are misleading, you appear to misinterpret the graphic you mentioned (which makes your comment misleading). Maybe Antarctica has fooled you but the split is not lopsided the way you claim. Basically all of Latin/South America uses the long scale except for Brazil, Guyana, Belize, and a dozen and a half small Caribbean islands. As the short scale plus milliard is a hybrid form, counting them to either side is insensible (and especially ludicrous since the common usage rarely extends to numbers where the difference to the long scale becomes apparent; so if anything, they are rather using the long scale). But even if we disregard them, the countries where the long scale is used outnumber and outman those using the short scale. 162.158.203.26 11:34, 23 June 2021 (UTC)
- Even the line containing the "In Britian" hyperlink does NOT say what the linked page actually states - that Britain uses the short-scale now, although they used the long-scale quite some time ago (before 1974). Ianrbibtitlht (talk) 14:58, 28 December 2018 (UTC)
Russian is a weird hybrid of short and long scale. We use milliard like long scale, then trillion like short scale. Not confusing at all :) 162.158.92.34 11:43, 3 January 2019 (UTC)
The line that includes "Though people in Britain often use the American definition as of the past few decades" is a bit misleading. In fact, the government of Great Britain announced, proclaimed, and declared that they will officially use the short-scale scheme in 1974. If you live there and are still using the long-scale system, then per your countries leadership you are wrong! The short-scale system is YOUR definition, not the American definition. Interestingly, we didn't invent the short-scale system because it was brought to the Americas by Europeans before the United States of America was even founded! We just continued to use it because it's all we knew until Randall came along and pointed out how screwed up the rest of the world is! Ianrbibtitlht (talk) 15:46, 28 December 2018 (UTC)
Long live scientific / exponential notation! 16:19, 28 December 2018 (UTC)~
Set the first tick on the y-axis to have value 0, and set the last tick to have value 5. Then, the y-values of all the y-axis ticks are 0, 1.0053, 1.9973, 3.0127, 3.9947, and 5, approximately as expected. (The x-axis is at y-value -0.9903.) Now, setting the x-axis as the base-10 logarithm, the points' coordinates are as follows: (6, 0.5388); (7, 2.4800); (8, 3.7672); (9, 1.8009); (10, 3.3622); (11, 4.2860); (12, 3.2495); (13, 4.1125); (14, 4.5939). LegionMammal978 (talk) 16:24, 28 December 2018 (UTC)
I'd even say that 999,999,999 (especially when worded in full) seems like a way bigger number than 1 billion, despite being one less. --108.162.229.28 16:42, 28 December 2018 (UTC)
The graph reminded me of number-form synaesthesia, which I have. My number shape (and most people's) is different though, and much more curly. Cosmogoblin (talk) 17:20, 28 December 2018 (UTC)
The way I keep track of this is to remember that 1 trillion is 1 million millions. So if the US current national debt (counting neither debt by the states nor unfunded future liabilities) is 23 trillion dollars, then you would need a million dollars from 23 million people to pay it off. The US total population is roughly 327 million. So you would need a million dollars from every 14th person (counting adults, children and babies). Considering that there are only 11 million millionaires in the US and only 172 thousand people with net worth over 25 million, we are in deep doo-doo. Clearly, not even the fantasy "tax the rich" is not going to help pay the future. Lack of number appreciation is going to kill us. Rtanenbaum (talk) 22:23, 30 December 2018 (UTC)
Many of you may be too young to remember the nuclear reactor incident at Three Mile Island [1]. There was a news broadcast at the time that stated that radiation of less than 5 rem (Roentgen Equivalent Man) was not considered biologically significant. He then went on to say that measurements at the plant showed 3,000 milli-REM, which was obviously (in his mind) much higher and extremely scary. In case you don't realize it, 3,000 milli-rem is 3 rem. In addition, some style guides recommend that you avoid the words billion and trillion. Australian scientific style guied. BradleyRoss (talk) 03:11, 31 December 2018 (UTC)
Comic No. 558, https://www.explainxkcd.com/wiki/index.php/558:_1000_Times is directly related to this one.162.158.154.133 08:29, 9 January 2019 (UTC)
Something not mentioned, and I think is relevant, is that part of the problem with the dashed regions is HOW you say the number. "500 million" might feel like more than 1 billion, because of the stated 500-vs-1 phenomenon, but someone might also say it as "half a billion", which would clearly feel like less (half is less than 1). And these dual terms don't appear until after the 100 mark - nobody would say "a tenth of a billion" or any smaller fraction. I'll leave this here a while, and if I think of it later I may add it to the description. NiceGuy1 (talk) 03:59, 26 January 2019 (UTC)
Log scales are for quitters who can’t find enough paper to make their point properly. Paralyzoid (talk) 17:49, 29 July 2019 (UTC)
What about quadrillions (and beyond)? Does the trend of the perceived size decreasing by less and less continue, or the perceived size stays approximately the same, or does it increase? 2001:4C4E:1C08:A700:6509:1E47:400D:BF05 20:52, 13 October 2025 (UTC)
- I personally tend to overthink quadrillions and beyond, to the extent of leaving myself only capable of comparing numbers explicitly described in the same terms. With billions and trillions, I might have a basic clue as to whether they're quoting short-scale or long-scale '-illions' (and they're 'only' factors of a thousand/a million different), but further beyond that the potential inconsitency gets absolutely absurd, with a thousand-million(/milliard, or 'billion' for those who use the far less justifiable naming system) just for whatever the quadrillion might mean. You've really got to start using some form of powers-of-ten notation by then (even if not before).
- On the other hand, when I was still learning about large numbers, I was under the impression that "a thousand thousands is a million (correct), a million millions is a billion (correct, at least to my current preferd scale), a billion billions is a trillion (no!), ...etc". Based upon that impression, every actual number-name (upon either basis) is drastically under-valued from all my original expectations. 2.98.65.8 21:21, 13 October 2025 (UTC)
 Add comment
Add comment
