113: Riemann-Zeta
| Riemann-Zeta |
 Title text: The graph is of the magnitude of the function with the real value between 0 and 2 and the imaginary between about 35 and 40. I've misplaced the exact parameters I used. |
Explanation[edit]
A prime number is any natural number with exactly two natural factors (1 and itself). The set of prime numbers is infinite, but they are somewhat elusive; there is no known way to find very large prime numbers except by trial and error. Some regularities in the primes have been found, but none that can fully predict their distribution.
The Riemann zeta function, errantly referred to as the Riemann-zeta function in the comic, is a function that takes in complex numbers and returns complex numbers. It is defined for Re('s')>1 as 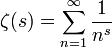 . For the rest of its domain (all complex numbers except 1), it is defined with analytic continuation. Its magnitude can be graphed in 3D, producing the "rippled curtain" referenced and depicted in the comic. There is a deep relationship between the Riemann zeta function and prime numbers, which makes the function a useful target of study for those attempting to understand primes.
. For the rest of its domain (all complex numbers except 1), it is defined with analytic continuation. Its magnitude can be graphed in 3D, producing the "rippled curtain" referenced and depicted in the comic. There is a deep relationship between the Riemann zeta function and prime numbers, which makes the function a useful target of study for those attempting to understand primes.
Here, Randall appears to be talking to his significant other, comparing her to prime numbers and himself to the Riemann zeta function. It is mathematically correct and quite poetic, until he mentions that his relationship differs from the comparison because "The Riemann-zeta function couldn't have given you herpes." This implies that he has infected his lover with an incurable venereal disease. The comic effect of an abrupt change in tone like this is known as bathos.
As the title text indicates, the graph in the picture is of the magnitude of ζ(s) for some section of the complex plane. Randall has forgotten the exact imaginary bounds of the graph, but he knows that the real axis goes from 0 to 2 and the imaginary axis goes from about 35i to about 40i.
Transcript[edit]
- [A z = fn(x,y) plot, with pointy spikes on the back sloping to a relatively flat front.]
- You are like the prime numbers
- Unpredictable turns, unconstrainable
- Tantalizingly regular but never quite the same
- I am like the Riemann-zeta function
- A rippled curtain of the imagined and real
- Deeply tied with you in ways incomprehensible
- Although, strictly speaking, The Riemann-zeta function couldn't have given you herpes
Discussion
[looking at the dearth of comments] Math is weird. -Kazvorpal (talk) 22:28, 19 September 2019 (UTC)
Wow, no one has anything to say here... 108.162.245.225 19:27, 19 November 2023 (UTC)