2088: Schwarzschild's Cat
| Schwarzschild's Cat |
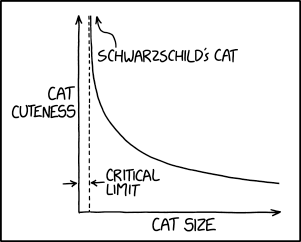 Title text: Cats can be smaller than the critical limit, but they're unobservable. If one shrinks enough that it crosses the limit, it just appears to get cuter and cuter as it slowly fades from view. |
Explanation[edit]
This comic is primarily a wordplay joke about the Schwarzschild radius, or the distance from a black hole corresponding to the event horizon.The Schwarzschild radius for a given body is the limit to which a given mass can be shrunk down before it becomes a black hole - the Schwarzschild radius also represents the event horizon of this newly-created black hole. The event horizon, in turn, is the limit from which nothing can leave a black hole; not even light. The joke is that, apparently, smaller cats are cuter, and there is a limit below which a sufficiently small cat (but larger than zero) will approach infinite cuteness, in a similar pattern to the way time's rate for an observer will approach infinity, the closer they get to the event horizon of a black hole.
It's also an oblique reference to the Schrödinger's cat thought-experiment, since the names (Erwin) "Schrödinger" and (Karl) "Schwarzschild" are somewhat similar and both men were early 20th-century physicists who exchanged ideas with Albert Einstein. However, the actual comic doesn't bring up quantum superposition.
The title text makes two allusions. First, it alludes to what happens when an object falls into a black hole. From an outside observer's point of view, such objects appear to slow down and take an infinite amount of time to cross the event horizon due to the time dilation of General relativity. The object's photons become increasingly red-shifted, fading as they lose energy to the black hole's gravity well. The scientific consensus suggests that from the falling object's point of view, it should continue to experience time and cross the Schwarzschild radius, but that event is unobservable from the outside (hence the term "event horizon").
Second, the title text is a play on the Cheshire Cat from Alice in Wonderland, which slowly fades from view until only its grin remains.
Randall previously discussed the superiority of tiny mammals in 1682: Bun, and drew graphs relating to the perceived cuteness of cats in 231: Cat Proximity.
Transcript[edit]
- [A graph is shown. The x-axis is labeled "Cat size" and the y-axis, "Cat cuteness". Parallel to and a short distance from the y axis is a dashed line the same length as the y-axis line, representing a vertical asymptote; the space between the y axis and the dashed line is labelled "Critical Limit". Graphed is a function coming down from infinity, starting close to the dashed line; it then levels off and does not reach zero on-screen. At the top end of the graph is the text "Schwarzschild's Cat" and an arrow pointing upwards outside of the graph.]
Discussion
This xkcd is self-referencing as the size of cute animals is referenced to in many comics like 1871, 1682, 1903--Gunterkoenigsmann (talk) 21:40, 22 December 2018 (UTC)
I think the biggest question is, what is that arrow on the left is pointing at? 162.158.146.82 22:46, 21 December 2018 (UTC)
- It is a common notation to have a gap or distance indicated by pairing two arrows. When the gap is small, the arrows go outside the reference lines and point inward. While it would be more correct to have the single arrow on the right pointing to the dotted line as the referenced critical limit, Randall has simply marked the entire range as the limit. Dúthomhas (talk) 16:40, 19 September 2025 (UTC)
This is likely a cross between the Schwarzschild Radius and Schrodinger's cat. Below the Schwarzschild Radius, you can't tell how cute the cat is because you can't see it, just like you can't tell if the cat is alive or dead in the box. Ianrbibtitlht (talk) 16:08, 21 December 2018 (UTC)
The title text has nothing to do with Hawking radiation - it's referencing a phenomenon that happens near a black hole's event horizon. As you observe an object falling toward the black hole, when it reaches the event horizon it appears to you to be frozen in place, and gradually fades to black. See https://www.youtube.com/watch?v=XE5PNbsUERE
- I agree - I was going to make the same comment. Ianrbibtitlht (talk) 16:34, 21 December 2018 (UTC)
However, Hawking radiation describes the decay of black holes and so the black hole would get smaller and smaller, but I believe that you are also correct. Gollum (talk) 16:32, 21 December 2018 (UTC)
For the title text, I thought of the Cheshire Cat. Elvenivle (talk) 23:31, 21 December 2018 (UTC)
- Presumably The Cheshire Cat is able to change its size at will in order to vanish. As this doesn't change its mass eventually it passes the Schwarzchild Limit, beyond which information cannot escape. This is why the Cheshire Cat, like Mona Lisa, has an enigmatic smile - it's not possible to know why it smiles, as that would constitute information transfer. Espatie (talk) 18:03, 22 December 2018 (UTC)
No offence Elvenivle, but I don't think this has anything to do with the Cheshire Cat. I vote we change it. 108.162.245.244 23:35, 21 December 2018 (UTC)
- I vote against. Wonderland has everything to do with quantum physics. -- Hkmaly (talk) 01:20, 22 December 2018 (UTC)
Going off on a tangent
Sorry, I know this has got nothing to do with explaining the above comic, but when I read the title text a thought struck me: if the cat is getting cuter and cuter as it shrinks, a cat lover will get happier and happier as it increases in cuteness. However there will be a point that the cat lover will become sadder as they realise that the cat is going to disappear from their view forever. I would be interested in seeing the curve of cat lover's happiness against cat size, and seeing if we can determine the optimum size for "Cat Cuteness".
And now, having defined the unit CC, I am never going to be able to watch a medical drama in the same way again... 141.101.98.46 10:23, 22 December 2018 (UTC)
So according to the graph, a tiger would have very little cuteness, which might be true if said tiger was in the process of attacking you for his lunch. Otherwise, there are lots of tiger videos on Youtube that could be easily described as cute. Nutster (talk) 16:57, 22 December 2018 (UTC)
I googled something like "how do black holes form if time stops at the event horizon" and found the variety of expert-sounding answers to be quite engaging, for example. The simplest explanation to me seems to be that the matter mostly just stays on the surface forever, from our perspective, but the top-rated answer from that link is that space-time curves so much that the matter is no longer traveling through space and instead is falling through time itself! A statement like that sounds really cool and likely true, but could use a reason backing it up. 172.69.62.232 21:58, 22 December 2018 (UTC)
I don't think that has anything to do with Schrödinger. Simply, the cat gets smaller until it's smaller than its Schwarzschild radius and it becomes a black hole, and so its size is determined by its Schwarzschild radius. --172.69.6.94 04:18, 24 December 2018 (UTC)
Another Tangent This isn't technically for the comic itself, but the Incomplete banner on this page was so funny that I just HAD to preserve it "This explanation may be incomplete or incorrect: Created by a SMALL CAT WITH NO CONCEPT OF FIELD EQUATIONS. Could use more information on the relevant theoretical physics. Do NOT delete this tag too soon. If you can address this issue, please edit the page! Thanks. " HackneyedTrope (talk) 08:21, 30 December 2018 (UTC)
Slightly Disappointing that no one posted a picture of a tiny kitty (one that could be on the leading edge of that critical limit). [[1]]. DurtyWilly (talk) 11:56, 3 January 2019 (UTC)
Schwartzchild's Cat is local maximum of smallness x cuteness. I think the Schwartzchild's Cat is the smallest (and therefore, cutest) a cat can be before making it smaller saddens the human because it's now too small.
An alternate theory is that the critical limit marks the point where the small cat has become so cute that it cannot be seen, because a larger, grumpier cat has mailed it to Abu Dhabi. -- C.Robin (talk) 01:05, 27 September 2020 (UTC)
It must be said that very large cats can also be extremely cute.
So really the graph has two areas in which it reaches infinity. But does this mean that tigers are now invisible, as they are past the second cute point? Redacted II (talk) 17:51, 28 November 2024 (UTC)