2118: Normal Distribution
| Normal Distribution |
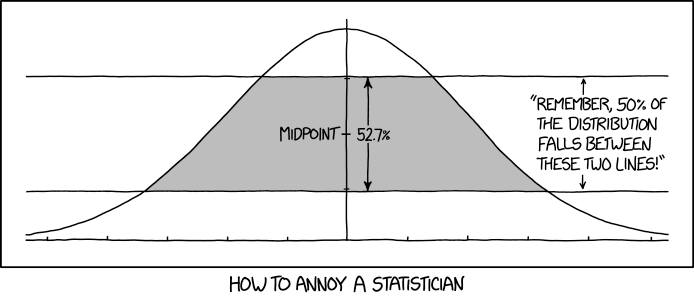 Title text: It's the NORMAL distribution, not the TANGENT distribution. |
Explanation[edit]
This is another comic on How to annoy people, particularly targeting statisticians in this instance.
In statistics, a distribution is a representation that can be understood in terms of how much of a sample is expected to fall into either discrete bins or between particular ranges of values. For example, if you wanted to represent an age distribution using bins of ten years (0-9, 10-19, etc.), you could produce a bar chart, one bar for each bin, where the height of each bar represents a count of the portion of the sample matching that bin. To turn that bar chart into a distribution, you'd get infinitely many people (technically: a number N which tends to infinity), put them into age bins that are infinitely narrow (technically: bins whose size is O(1/sqrt(N))), and then divide each bin count by the total count so that the whole thing added up to 1. It is common to ask how much of the distribution lies between two vertical lines; that would correspond to asking what percent of people are expected to fall between two ages.
Many statistical samplings resemble a pattern called a "normal distribution". A theoretically perfect normal distribution would have an infinite sample size and infinitely small bins. That would produce a bar chart matching the shape of the curve in the comic.
The area between two vertical lines of the distribution represents the probability that a randomly selected X-value is between the X-values of the lines. Randall instead finds the area between two horizontal lines, which is mathematically meaningless, because the Y-axis of a probability distribution is typically taken to represent magnitude as a fraction of unity. In the age-distribution analogy above, two points with the same X-value could be understood to represent two people with the same age; but two points with the same Y-value cannot easily be understood in terms of the analogy. The items "represented" by the magnitude at any given horizontal position are indistinguishable, unordered, and interchangeable; the fact that two items happen to fall at the same position on the Y-axis doesn't mean they have anything in common.
In short, Randall has invented a new probability distribution, which the title text humorously implies should be called the tangent distribution. This distribution is defined as follows: consider the area between the curve in the comic and the horizontal axis, and consider a random point (X, Y) uniformly distributed in that region. Then X has the normal distribution and Y has the tangent distribution. Areas between vertical lines in the comic give probabilities concerning X, and areas between horizontal lines in the comic give probabilities concerning Y. The comic correctly indicates that if we let R be the interval of Y values that is 52.682% of the range of Y centered at the midpoint of the range, then any randomly selected Y value has probability 1/2 of falling inside interval R.
This distribution has never been discussed before, and has no known application. Moreover, the distribution of Y is not symmetric: while 50% of Y values fall inside interval R, 41% fall below R and only 9% fall above R. So the single piece of information in the comic is not a good way to describe this distribution! We do use such intervals for the normal distribution because the normal distribution is symmetric, and the center of symmetry is the mean, median, and mode. (However, it would be just about as ridiculous to observe that 50% of the X values in a standard normal distribution fall between the vertical lines X=-0.2 and X=1.41.)
The title text refers to the notion of normals and tangents in geometry. Given a 2D curve or 3D surface, a line which points perpendicularly outward from a point on the curve or surface (making a 90-degree angle with the curve) is said to be normal to the curve, while a line which just grazes the curve, being exactly parallel to the curve at the point of contact, is said to be tangent to the curve at that point. The joke is that this geometrical notion of normal is completely unrelated to the statistical normal distribution. Randall observes that if you take a geometric normal and rotate it 90 degrees, you produce a tangent; thus, if you take the normal distribution and rotate it by 90 degrees, you must get something called the "tangent distribution." Saying this to a statistician would only annoy the statistician further.
This is annoying to a statistician not only because the terms normal and tangent come from differential geometry and have no established meaning in probability theory. Even the word perpendicular has no established meaning in probability theory. Of course, the x and y coordinates in the comic are perpendicular (orthogonal) coordinates, but X and Y are not "perpendicular" or "orthogonal" random variables. Even if we give "perpendicular" or "orthogonal" a probabilistic meaning, and the most obvious such meaning is either independent, which even uses a symbol related to the geometric symbol for perpendicularity, or uncorrelated, which makes X and Y orthogonal vectors in the Hilbert space of random variables that are square integrable with respect to Lebesgue measure, X and Y are not perpendicular in either of these senses.
So the more probability and statistics you know, the more annoying this comic becomes. It is not just about confusing novices.
Transcript[edit]
- [A bell curve of a normal distribution, with the area between two horizontal lines shaded.]
- [The center of the chart is marked between the two lines:]
- Midpoint
- [The distance between the lines is marked to the right of the midpoint, with the label:]
- 52.7%
- [A label on the outside of the graph, describing the distance between the two lines:]
- "Remember, 50% of the distribution falls between these two lines!"
- [Caption below the panel:]
- How to annoy a statistician
Discussion
Is there a statistician in the house? Hawthorn (talk) 15:32, 1 March 2019 (UTC)
I think they all got annoyed at the graph and left. Margath (talk) 15:46, 1 March 2019 (UTC)
Of course there is! 162.158.214.22 15:44, 1 March 2019 (UTC)
As an example: When measuring the height of people in the same age bracket, then you'll expect the number of people at each height to look like this graph. There will be a lot of people around the average height, fewer a foot shorter/taller, some (but very few) exceptionally tall people, and some (but very few) exceptionally short people. The x-value represents the height, the y-value essentially represents the amount of population that share that height. When we measure the middle 50% of the population using vertical bars, then people at a certain height are either inside OR outside the middle. Randall uses horizontal bars here, which means some people at a certain height will be counted in the middle 50%, but other people with the same height won't be. In fact, some people with the exact average height of the whole population would fall outside the middle. 108.162.241.214 16:01, 1 March 2019 (UTC)
Feel free to rip me apart for referring to it as the "number of people at each height", since y-axis is more complicated than a simple count. 108.162.241.214 16:03, 1 March 2019 (UTC)
Just to say, Randall's horizontal slice isn't entirely meaningless. It's a calculation I've had to do, where I have a series of binned samples of a population (say I knew how many fell in -10..10, how many fell in -5..5, how many fell in -2..2) and wanted to combine them with an appropriate weighting to approximate a Gaussian. I was using it for filtering, but it's logically similar. Fluppeteer (talk) 16:19, 1 March 2019 (UTC)
- Also, the slice sampler for MCMC is a trick for sampling from a distribution by "turning it on its side". But I don't think the 50% figure would be meaningful in that context. (Though the 52.7% number on this graph would be.) 172.68.54.136 21:16, 1 March 2019 (UTC)
Pedant: etymologically, there *is* actually a connection between a normal (to a surface or line) and the normal distribution; the former comes from the Latin for a set square (giving you perpendicular), and it later came to mean "standard". The "tangential distribution" certainly fits the etymology of "odd/unusual" though. Fluppeteer (talk) 16:26, 1 March 2019 (UTC)
This reminds me of the difference between Riemann(-Stieltjes) and Lebesgue integration. 172.68.54.160 20:16, 1 March 2019 (UTC)
As the axis are not labeled (see comic 833) we could consider this a multivariate distribution where one parameter is uniform and the other is normal. That was my first thought when I saw this. 172.68.34.88 18:43, 1 March 2019 (UTC)
Is there any meaning to midpoint: 52.7%? Maybe that is the arbitrary center he formed the horizontal bounds around? Maybe it relates to data? Is this a reference to something? It's certainly reminiscent of how normal distributions produce statistically meaningful numbers that have weird decimals in them (like the % represented by being within so many standard deviations). 162.158.78.178 19:45, 1 March 2019 (UTC)
- Maybe it's because the meaning of "50% of the chart lies between these lines" specifically becomes roughly useless for discerning error if the lines are not centered around the origin. 162.158.78.178 19:52, 1 March 2019 (UTC)
- I might get it!!! The area between the lines is 52.7% of the total area: which means that 50% is technically included in what lies between them. 162.158.78.220 23:07, 1 March 2019 (UTC)
The correct way to do this is to have the topmost vertical line equal to or above the top of the normal plot. Then the bottom-most line would represent the same values as vertical lines would. 162.158.78.220 23:32, 1 March 2019 (UTC)
Say I want to build a diverse team or a representative council. And it is more important that the selection is representative of several subpopulations (who should not be voted down by the majority) than that it gives an equal fair chance to anybody. I would cut away the absolute outliers and reduce the weight of the most abundant group - this gives just the area between the two lines. Sebastian --172.68.110.70 23:40, 1 March 2019 (UTC)
- That's actually... not a horrible idea. Problem is, it's not robust to transformations of the X axis, because of the Jacobian multiplier that comes with such transformations. Which in practice would look like people loudly insisting they have nothing in common with each other ("we wear baseball hats with the brim to the RIGHT while those other completely unrelated people wear them with the brim to the LEFT")162.158.63.244 16:26, 2 March 2019 (UTC)
Has somebody measured or calculated (by assuming normal distribution) the areas? It seems that the upper area is way smaller than the lower one, but both having the same 'height' in the middle. Is the 52.7% graphically correct? I tried half of the height at 0: .398942 and integrated, then I get 52,6% for the white area and 47,4% for the gray area. On the y-axis it seems that the three visible ticks are .1, .2, .3, then the gray area would be a bit broader than .2 and centered at .1. Sebastian --172.68.110.70 23:40, 1 March 2019 (UTC)
Got Nerd Sniped by the number "52.7%", but failed on an analytic solution and settled for a quick and dirty numerical integration instead, which suggested that the exact number might be somewhere between .5268 and .5269, so I think I'm not far from the truth. As I see it, the shaded area is vertically centered around the vertical midpoint, with a relative vertical width chosen such that the shaded area is exactly 50% of the total area under the curve. Just as usual, only with vertical instead of horizontal binning, which of course is the twist that makes this graph puzzling, funny, and completely useless for meaningful interpretation. The label "52.7%" is not an addition to the Midpoint label but instead gives the width of the vertical bin, as a percentage of the vertical height of the curve. I read the tics on the vertical axis to indicate just quarters of the curve maximum, which is consistent with my understanding of "Midpoint". Oh, and you are certainly right in that the marginal distributions at the top and the bottom are asymmetric, as is the gaussian when viewed sideways. 172.68.110.64 23:56, 1 March 2019 (UTC)
- Feh. You merely have to integrate something like Sqrt[Log[x]] which I'm too lazy for and use Mathematica instead which gives...<covers eyes>...what was #2117 about again? 162.158.94.2 11:57, 2 March 2019 (UTC)
- There's a way to (attempt to) symbolically integrate functions involving things like e^(-x^2) like you have with the normal distribution (Cherry's extension of the Risch algorithm, see his thesis or his 1985 paper), but I have no idea how to apply it here. It's definitely a very complex procedure. As I understand even Mathematica has not implemented it in full. - CRGreathouse (talk) 03:59, 3 March 2019 (UTC)
- I found this calculation of the number 52.7% from wolfram community. https://community.wolfram.com/groups/-/m/t/1623478 I found the area subtraction diagram near the middle most useful for understanding the basic idea of it. Also, a related question in quora. https://www.quora.com/In-the-xkcd-comic-Normal-Distribution-how-was-the-number-52-7-calculated Lamty101 (talk) 08:21, 21 August 2020 (UTC)
- There's a way to (attempt to) symbolically integrate functions involving things like e^(-x^2) like you have with the normal distribution (Cherry's extension of the Risch algorithm, see his thesis or his 1985 paper), but I have no idea how to apply it here. It's definitely a very complex procedure. As I understand even Mathematica has not implemented it in full. - CRGreathouse (talk) 03:59, 3 March 2019 (UTC)
How to annoy a Democratic Liberal Statician- Point out that every identity group that they're trying to make "normal" falls to the far left or the far right of the normal distribution curve.Seebert (talk) 14:50, 2 March 2019 (UTC)
- As somebody who happens to be all 3 of those things, I can confirm that your comment annoyed me. But only for bringing politics into a discussion that isn't political, and for misusing "normal" in a way like Randall's alt-text. The actual "edgy" political content of your post I find wrong but not particularly annoying. YMMV. 162.158.63.244 16:26, 2 March 2019 (UTC)
- All statistics are ultimately political, in that they are used to politically argue for predetermined conclusions. Statistics aren't very useful at actually discovering anything not previously determined to be true. And it isn't me has misused the word normal, it's those ~2% of the population identity groups that are now using the courts to claim to be normal, when mathematically, they'll never be normal.Seebert (talk) 15:14, 3 March 2019 (UTC)
"Completely meaningless?"
The explanation currently says, "Randall finds the area between two horizontal lines instead, which is mathematically completely meaningless." This doesn't seem right. Each of the two horizontal lines intersect the curve at points and those points have meaningful values on the x axis. I'm not sure if they represent anything interesting (or rather, what their significance might be), but the result is the horizontal lines are not meaningless. I'm a little reluctant to edit it because I'm not sure how meaning to ascribe (and I also haven't measured the or calculated what those points are), but the explanation as-written seems improper. Do I have it wrong? JohnHawkinson (talk) 15:02, 2 March 2019 (UTC)
- Nothing is ever completely meaningless. I think the change to "completely meaningless" may have been added by an annoyed statistician. I wrote the previous phrasing of it rarely being used for anything meaningful, so it seems impolite for me to edit it back. It's notable that implying there is meaning to the horizontal lines could be misleading to those new to statistics. It's also notable that the area between them represents a calculable portion of the samplesets, and that the points of intersection are just as meaningful as with vertical lines, two uses mentioned in comments above. 162.158.79.245 15:13, 2 March 2019 (UTC)
The horizontal division is vaguely reminiscent of Lebesgue integration. I wonder if that was intentional. Dfeuer (talk) 06:37, 3 March 2019 (UTC)
There is now a statistician in the house. I have added two paragraphs that discuss some of the fine points. This is wrong (which, of course, Randall knows) in so many ways! I tried to keep what I said simple, but it may need some expansion. I also don't think we need the graphic in the explanation because, as I say in the text I added, that is the wrong way to describe a nonsymmetric distribution like the "tangent distribution". Cjgeyer (talk) 22:56, 3 March 2019 (UTC)
Sloppy explanation
What I don't like, are phrases like: "To turn that bar chart into a distribution, you'd get an infinite number of people, put them into age bins that are infinitely narrow, [...]". Infinitely narrow is actually zero or 0. No other interpretation exists.
Pictures
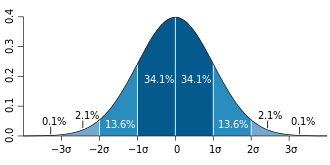
Hey @Zom-b, you changed the picture I set and gave the comment "I don't know what that other curve is, but it's not normal. (no) pun intended." The two pictures appear to have exactly the same curve in them. I was wondering what you meant by your comment? This is the first picture I've ever set in a wiki, and I worry I could have made an error. Here are the two pictures:
![]() . I like the first one, mine, because the lines extend beyond the graph as Randall's do. I like the second one, yours, because it includes percentages over the graph as Randall's has. But the curves both appear normal, in both senses, to me? 162.158.79.113 13:05, 5 March 2019 (UTC)
. I like the first one, mine, because the lines extend beyond the graph as Randall's do. I like the second one, yours, because it includes percentages over the graph as Randall's has. But the curves both appear normal, in both senses, to me? 162.158.79.113 13:05, 5 March 2019 (UTC)
- Regarding "infinitely narrow", I disagree that this is sloppy wording; it is concisely describing something that tends to zero at the limit of infinity, which is useful information. Hawthorn (talk) 10:26, 20 March 2019 (UTC)
 Add comment
Add comment
