2311: Confidence Interval
| Confidence Interval |
 Title text: The worst part is that's the millisigma interval. |
Explanation[edit]
This is another one of Randall's Tips, this time a Science Tip. This is the second time that a category of tips (with the first being "Protip") has been re-used.
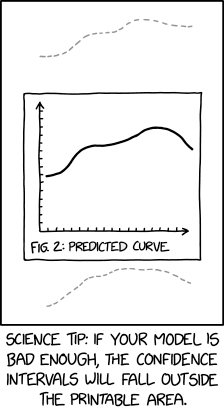
Graphs of continuous functions' predicted values often show confidence intervals, a region (either shaded or marked with dotted lines, the latter used here) that indicates the margin of error for the prediction at any point. The joke in this comic is that the estimate has so much uncertainty that the confidence interval extends off the top and bottom of the chart, which in a real report would usually prevent it from being printed and require a re-scaled chart to show it (if not declined altogether, as data with such wide variance might be deemed useless). This may be a tip as if it's outside the printable area, it won't be seen by anyone who reads it, and thus they won't realize how bad your model is, though this is more of a tip in how to trick people into falsely thinking you've shown a good result with your work than it is a tip in presenting an actual legitimate useful scientific result.
In the title text, a millisigma would be an error of +/- 1/1000th of a standard deviation. Statistical error and uncertainty is typically measured by standard deviation, which is written in formulas with the Greek letter sigma, and is also frequently referred to by the word "sigma." Measurements of sample means, one of the most common experimentally determined variables, will tend to follow a normal distribution, such that 68 percent of members of the population will fall within one sigma (plus or minus) of the mean value, 95 percent within two sigma, and 99.7 percent within three sigma. Any of these intervals may be usefully reported as the confidence interval, so long as it's made clear to the reader, but two- or three-sigma are sufficient for most applications. However, this graph shows data of such poor quality (or such poorly-chosen y-axis bounds) that even the millisigma confidence interval (0.08% of the population -- not often used in science, but occasionally found in e.g. molecular analysis tools) does not fit on the graph. Variations in the curve that are small compared to the error bar typically can't be distinguished from errors. Therefore, the shape of the curve - and the entire graph in this example - is meaningless.
Transcript[edit]
- [A graph is shown in the middle of the panel with a square frame around it. The graph has two unlabeled axes with ticks along both axes, and the axes end in arrows. A solid line graph is shown starting around the middle of the Y axis, going up and flattening twice before falling down towards the right. Far above and just below the frame around the graph are two gray dotted lines, following the same trend as the original but not identical copies.]
- Fig. 2: Predicted Curve
- [Caption below the panel:]
- Science tip: If your model is bad enough, the confidence intervals will fall outside the printable area.
Discussion
What's a millisigma? 162.158.107.209 03:31, 26 May 2020 (UTC)Ven
- Not an official scientific term - most likely referring to standard deviation. One standard deviation, or sigma, is the 68.3 % of values lying around the mean in a normal distribution. A millisigma in a standard deviation would be .0683 % of a normal distribution so that much variation would be bad? Not sure. 172.69.63.203 05:23, 26 May 2020 (UTC)
- Actually, if you integrate a normal distribution
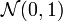 from
from 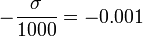 to
to 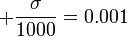 , you'll get a range of about 0.08% of all values. This would be bad because it would mean that, as big as the confidence interval appears in the picture, the more meaningful 1- or 3-sigma interval (whose size represents the uncertainty of the model) would be larger by a factor of 1250 or 3750, respectively. --Koveras (talk) 08:38, 26 May 2020 (UTC)
, you'll get a range of about 0.08% of all values. This would be bad because it would mean that, as big as the confidence interval appears in the picture, the more meaningful 1- or 3-sigma interval (whose size represents the uncertainty of the model) would be larger by a factor of 1250 or 3750, respectively. --Koveras (talk) 08:38, 26 May 2020 (UTC)
- Actually, if you integrate a normal distribution
- Perhaps you heard about Six Sigma, a quality method used by General Electric (among others) to keep specifications and processes within tiny tolerances. The six sigmas mean that even absolute (so-called) outliers in your production are within the strict tolerances. With milli-sigmas it is extremely seldom to get an acceptable result at all. Sebastian --108.162.229.234 10:53, 26 May 2020 (UTC)
Can it be related to Covid19 pandemic and all those graphs that try to predict if it is in decline or not? Tkopec (talk) 08:27, 26 May 2020 (UTC)
- I didn't think so, until I read the discussion of Millisigma above, and realized that the millisigma is awfully close to your chance, worldwide, of dying from COVID-19. A millisigma of the population will die.Seebert (talk) 14:56, 27 May 2020 (UTC)
- No. But maybe it's related to the recent Mt. St. Helens comic... :p Seriously, not everything has to be related to the hot-button topic of the day.
- Au contraire, mes amis, it is obvious to me that 1: Barrel - Part 1 is about socially isolating away from the virus. (Remember to sign?) 162.158.158.237 10:56, 26 May 2020 (UTC)
Isn't the (or a) reason that this is a science tip is that having confidence lines are off the page makes it look as if the prediction is precise? 141.101.99.65 11:35, 26 May 2020 (UTC)
Real life example of this comic (scroll down to Alaska, Hawaii, Montana, etc): https://rt.live/ Godzilla (talk) 15:26, 26 May 2020 (UTC)
The smaller the error or uncertainty value, the larger the confidence number. A confidence value of less than 1 is usually considered unreliable, but may justify further experiments/observations. Confidence that is practically indistinguishable from 0 means the result is only marginally better than pure chance or a result showing no correlation. Said another way, you have no confidence in your observations. Nutster (talk) 13:41, 26 May 2020 (UTC)
Doesn't it bother anybody else that the inside of the P, R and D characters are filled with gray in the comic? Divieira (talk) 17:43, 22 June 2020 (UTC)
Suggestions for improvement on the shape of the two confidence intervals[edit]
The confidence interval of interpolation (usually just the "confidence interval of prediction," not the confidence of the mean, but that's another story) should not be confused with the confidence interval of extrapolation, which should be called the "confidence interval of prediction" if the confidence interval of the curve fit wasn't called that.
https://imgur.com/gallery/dBvxzxF
I think mathematicians and cartoonists need to team up to fix this. 172.68.142.47 17:57, 26 May 2020 (UTC)