3010: Geometriphylogenetics
| Geometriphylogenetics |
 Title text: There's a maximum likelihood that I'm doing phylogenetics wrong. |
Explanation[edit]
|
This explanation may be incomplete or incorrect: Created by CLOSE BOT RELATIVE - Please change this comment when editing this page. Do NOT delete this tag too soon. If you can address this issue, please edit the page! Thanks. |
Data for phylogenetic analyses may come from any attributes ("characters") of the things being examined. Rigorous techniques for these analyses became available starting in the 1950s, and these replaced earlier methods based largely on the individual judgement of experts. In phylogenetic studies of organisms, their DNA is far and away the most data-dense source of information, and consequently, most present-day investigations are based on analyses of selected genes and, increasingly, whole genomes. Thanks to the advent of more robust datasets, and more robust methods of data analysis, it is now commonplace for studies, especially on relatively understudied creatures, to reconstruct an evolutionary history (a phylogeny) that is radically different from what had previously been assumed. This is the "phylogenetic revolution" referred to in the caption. One example is the genus Hippopotamus, which had been considered a relative of pigs, which the animals somewhat resemble, until modern data and methods revealed it to be more closely related to whales, despite the animals being very different physically (hippos spend time in water, but can't swim).
This comic presents a tree, which resembles and purports to be a phylogenetic tree, in which the endpoints ("terminal taxa") are geometric shapes. This has been given the name "geometriphylogenetics" — a portmanteau of "geometry" and "phylogenetics". The claim is that triangles have been moved from the lower part of the tree (where they would be closely related to squares, rectangles, pentangles, and the like) to the upper part (placing them closer to circles and ellipses). This is a riff on the findings, and even the wording, of authentic phylogenetic research papers that report "revolutionary" results. The absurdity, and the joke, is that geometries do not change over time. Human understanding might change, but triangles and circles and rectangles themselves did not evolve or descend from ancestors, they are not progeny of some other geometries of ages past, and therefore phylogenetic principles and techniques don't apply to their study. Moreover, geometries do not contain DNA,[citation needed] so genetic analysis, even if it was ever relevant, is impossible.
The title text alludes to maximum likelihood, one of the most robust, and most frequently used, methodologies for phylogenetic analysis. The method builds a number of trees from the data, assigns to each a probability that it conforms to a pre-selected model of evolution, and then selects the tree that has the highest (maximum) likelihood of conformity to the model. In this case, though, the statement "There's a [high probability] that I'm doing phylogenetics wrong" doesn't just have the maximum probability of the available options; it has the maximum possible probability of 1, because it is definitely the case.
Transcript[edit]
|
|
This transcript is incomplete. Please help editing it! Thanks. |
- [A tree diagram, or a dendrogram is shown, consisting of lines that branch off from left to right, starting with one horizontal line on the left. Eight results are shown on the right: ellipse on Path 1, circle on Path 2, triangle on Path 3, parallelogram on Path 4, trapezoid on Path 5, square on Path 6, rectangle on Path 7, and a pentagon on Path 8. The paths are listed in order top to bottom.]
- [Path 3 and the triangle are bold black, while the other branches are dimmer. The paths are connected as follows: Path 2 and 3 are connected, then both connect together to Path 1; Path 4 and 5 are connected, as are Path 6 and 7, and these two paths are connected altogether; Path 8 is then connected to the branch containing Paths 4 to 7. All of Paths 1 to 3 are then connected to Paths 4 to 8, the branches all culminating in a single line on the left.]
- [Caption below the panel:]
- The phylogenetic revolution continues:
- Triangles were long believed to be related to squares, but genetic analysis proves that they are actually very pointy circles.
add a comment! ⋅ add a topic (use sparingly)! ⋅ 
refresh comments!Discussion
Does the phrase "maximum likelihood" have any relationship to phylogenetics? Ianrbibtitlht (talk) 03:01, 12 November 2024 (UTC)
- Profoundly so. Most contemporary analyses, especially of large datasets, use either maximum-likelihood methodologies or Bayesian inference (q.v.). I will see if I can say something coherent and comprehensible about this in the explanation. 172.71.147.58 03:30, 12 November 2024 (UTC)
- If it was you who added the explanation for the title text, nicely done! Ianrbibtitlht (talk) 05:04, 12 November 2024 (UTC)
"Pointy circle" is, of course, an oxymoron. Randall is also making a joke about how older phylogenetic trees were based on anatomy, like saying that squares and triangles are close because they have exoskeletons with straight lines and joints. Now, the tree is (where possible) based on genetic similarity. Nitpicking (talk) 05:10, 12 November 2024 (UTC)
Hippos can't swim? Did the BBC lie to us? https://youtu.be/X20NjqMiQyo?si=8pN-xwgKJEWM08ZF 172.68.186.135 06:18, 12 November 2024 (UTC)
Why was phylogenetic analysis required to establish this relationship? Reuleaux triangles are an intermediate form, demonstrating a close relation between circles and triangles. 172.71.130.208 06:24, 12 November 2024 (UTC)
Obviously, he's doing phylogenetics wrong: the pentagons (& hexagons, not shown) should also be shown as descending from the circles. Plus, the ovoids (far more than a middle step between lentiform & triangle, truly an extant branch in their own right) are not represented at all. A major oversight, to cut such corners, given the point he's circling about? ProphetZarquon (talk) 06:31, 12 November 2024 (UTC)
- There are two competing theories of the origin of circles. They are either very basal polygons (having one side) or very derived (having infinite sides). It's possible that both are true and 'circle' is a polyphyletic group. RegularSizedGuy (talk) 16:19, 12 November 2024 (UTC)
- Circles are priests, obviously. 172.69.43.183 23:46, 12 November 2024 (UTC)
Someone should add something about how circles and triangles are related through trig in a way that the rest aren't. Sorry I am new to this and don't know how to format my comment correctly.
I'm sure you could develop a 'DNA' sequence for geometric shapes. [Number of active vertices + angle, Number of curves in each side + variation from straight + orientation from centre, thickness of stroke, etc] basically the sort of data in any drawing data of said shape. Thus you could have two circles that look every similar, but one being an extreme Reulaux triangle and the other a 10,000 sided polygon with no side curvature at all! C.f. Swift and swallow! YMMV RIIW - Ponder it (talk) 10:38, 12 November 2024 (UTC)
- The result would be a taxon x character data matrix, the first step in all forms of phylogenetic analysis. On such a small matrix, you could probably perform maximum parsimony analysis by hand, as Hennig did. However, with such a small number of characters per taxon, taxon resolution would probably be low (lots of polytomies instead of fully resolved dichotomies), and bootstrap support values would be horrible. The resulting consensus tree would likely be [ahem] sharply criticized - not least because it would be a "mere" similarity analysis and not a true phylogeny (not a reconstruction of descent with modification of progeny). Do not submit such a tree for peer review, and especially do not take it to a meeting of the Willi Hennig Society. You have been warned. 162.158.42.130 13:56, 12 November 2024 (UTC)
- I’m reminded of the incircle and circumcircle of a triangle. Triangles are the only shape where all polygons of that edge count are guaranteed to have an incircle and a circumcircle (unless, of course, it is degenerate). 172.71.24.5 13:34, 12 November 2024 (UTC)
Sorry, but I don't believe in this "Theory of Polygon Evolution". I believe all abstract polygons were created in their current state by intelligent mathematicians. Mathmannix (talk) 12:21, 12 November 2024 (UTC)
- Heathen - The One True Creator is Euclid! 😉 RIIW - Ponder it (talk) 12:38, 12 November 2024 (UTC)
Reminds me of pedigree genetic charts as well, anyways you geomreationists are so absurdly wrong it's laughable /j 108.162.238.130 13:24, 12 November 2024 (UTC)
Obviously both triangles and squares descended from circles. But, while triangles evolved from circles with protrusions that extended into points for improved dynamics, squares evolved from circles that developed flattened sides for more stability. Looking forward at their descendants, we see that both shapes have crab-like descendants. But again, developed from very different mechanisms: The evolved triangles's points split and reformed into the crab claws, while the squares evolved into rectangles which developed concave ends that eventually consolidated into the crab claw shape. 2314: Carcinization 162.158.41.73 20:11, 12 November 2024 (UTC)
It also reminds me of the quadrilateral family tree (google it, I guess), which has always bothered me exactly because it shows just how unapplicable phylogenetics is to geometry, or they are just super incestuous in a time-traveling sort of way? 172.70.43.29 20:14, 12 November 2024 (UTC)
- Also (re-)interbreeding. c.f. parallelograms that (regularised) become rhombi, but also the "kite" branch can lead, by regularising, to a rhombus. And rhombi descend to the special case of squares, as do special cases of rectangles (differently special cases of parallelograms than rhombi). If anything, the most interesting sub-family of quadrilateral are all the ones that (while not self-intersecting, adding further complications) manage not to be a rhombus, parallelogram or trapezium. 172.69.43.183 23:46, 12 November 2024 (UTC)
Circles are descended from polygons and squares are descended from triangles, at least according to the renowned expert Edwin Abbott Abbott. 172.71.175.23 21:48, 12 November 2024 (UTC)
Exciting new research may have found the universal common ancestor, which is being called a 'point'.172.70.86.111 09:32, 13 November 2024 (UTC)
If anyone would like to peer review me, I've filled in the "missing links" https://jimmysfiles.com/misc/evolution-of-shapes.png 172.69.194.78 (talk) 10:18, 13 November 2024 (please sign your comments with ~~~~)
- Nice! I did a very different ancestor reconstruction. Not to take any of this too seriously, but making an ancestor that is intermediate between the descendants (as in your triangle subtree) is rarely parsimonious because it requires mutations on both branches. So I end up with a circle as the root. I do like what you did with the quadrilaterals though, where changing an angle or side length counts as a mutation. Maybe angles are more fundamental in shape DNA than concepts like parallel and symmetric; who knows?
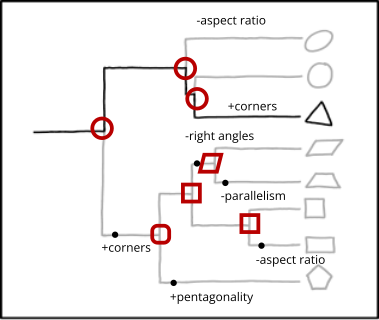
- --Quantum7 (talk) 13:44, 14 November 2024 (UTC)
- Is this a flatworld reference?
Intentional or unintentional, treating geometric shapes as related life forms is quite reminiscent of flatworld. 172.68.245.207 (talk) 14:33, 14 November 2024 (please sign your comments with ~~~~)
- Probably not, as it flat-out (npi!) contradicts the known lore of Flatland (if that's what you meant), without even obviously deliberately and knowingly doing so. It's just a general geometry thing, of which Flatland is a different branch of parody entirely. 162.158.74.69 15:26, 14 November 2024 (UTC)
