Talk:2070: Trig Identities
I am confused by the insect line. This seems to be true only if s=t.
141.101.96.209 19:03, 9 November 2018 (UTC)
- I added a note regarding how similar it sounds to 'sinsec'. 172.68.51.154 01:47, 10 November 2018 (UTC)
- That one and the `cas` aren't making any sense to me. GreatBigDot (talk) 20:02, 9 November 2018 (UTC)
- Oh, the casinus is much important to... What was it? --Dgbrt (talk) 20:15, 9 November 2018 (UTC)
- cas is realtively easy... it is cos(theta)=a/c -> cs(theta)=ao/c -> cas(theta)=o/c; when you realise that the top one isn't zero but o it clicks 141.101.96.209 23:35, 9 November 2018 (UTC)
- You made the same error Randall did: you divided by 'o' on the left and multiplied on the right. I think the theme of the page is expanding significantly upon common math errors that were already humorous, like the common proof of 5=3 by dividing and multiplying by zero. The error here is in line with the theme of casual beginner errors. 172.68.51.154
- You can see cin is derived from sin by swapping the positions of c and s. Likewise, Switching the a and o in cos(theta) = a/c gives cas(theta) = o/c i.e. no need for multiplicative consistency. The rule of treating things as a product of terms is implemented fully in the following lines. 162.158.91.83 11:23, 12 November 2018 (UTC)
-
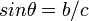 leading to
leading to 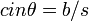 is algebraically valid if you interpret sin as the product of s, i, n by multiplying both sides by c/s. It is not valid to just "swap" two letters in one equation that is part of a system of equations. You could do the same trick and get
is algebraically valid if you interpret sin as the product of s, i, n by multiplying both sides by c/s. It is not valid to just "swap" two letters in one equation that is part of a system of equations. You could do the same trick and get 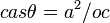 from
from 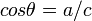 or start with
or start with 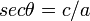 and get
and get 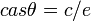 . Note for all equations except
. Note for all equations except 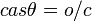 and switching an
and switching an  to a
to a 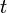 to find
to find 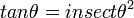 , the equations can be correctly derived by treating trig functions as product of single letter variables and algebraically manipulating them. Jimbob (talk) 16:59, 12 November 2018 (UTC)
, the equations can be correctly derived by treating trig functions as product of single letter variables and algebraically manipulating them. Jimbob (talk) 16:59, 12 November 2018 (UTC)
-
Is Enchant at target a magic:the gathering reference? AncientSwordRage (talk) 20:55, 9 November 2018 (UTC)
- I think it is a Magic: The Gathering reference. Although it is phrased oddly. You'd think it would be "at target enchantment", rather than "target at enchantment". --Dryhamm (talk) 21:04, 9 November 2018 (UTC)
- Likely, it refers to the bigbox retailer, Target. 172.68.58.233 (talk) (please sign your comments with ~~~~)
- To me it sounds more like a reference to a nerdy video game, where a certain object worked like this, turning e.g. BEAM OF DARK ENERGY into a BAKED FERRY GNOME 108.162.246.11 21:53, 12 November 2018 (UTC)
- Likely, it refers to the bigbox retailer, Target. 172.68.58.233 (talk) (please sign your comments with ~~~~)
- Voila - s=t. -- Elliott (talk) (please sign your comments with ~~~~)
- That was incredible! (assuming previous poster discovered the extrapolated proof in the description) 172.68.51.154 01:47, 10 November 2018 (UTC)
- Combining
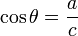 and
and 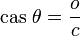 allows you to conclude
allows you to conclude 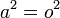 , not
, not  . 162.158.146.10 (talk) (please sign your comments with ~~~~)
. 162.158.146.10 (talk) (please sign your comments with ~~~~)
Somebody added a comment on puns, e.g. that "cin sucks". More explanation is needed. It looks like some kind of a meta-joke. If you ask why, and start interpreting, you see that "b/c" == "because". It might be the answer to why the puns line should be removed, though. 172.68.51.154
For the Bot->Boat->Stoat line, this comes from the word game where you add/change letters to make a new word. Start with bot=a/c, multiply by a on both sides gets boat=a^2/c. Multiply by st on both sides and divide b on both sides gets Stoat=a^2/c*St/b. 162.158.78.166 (talk) (please sign your comments with ~~~~)
Uh... people... THE NAME GAME? Hello? https://en.wikipedia.org/wiki/The_Name_Game 162.158.79.107 (talk) (please sign your comments with ~~~~)
Checking through the math, just working from the real trig identities, without considering Randall's at-first-glance questionable identities like cas theta = o/c, basically everything that does not have a factor of d or 2 in it is equal to 1, and d is equal to 1/2, which then establishes the more questionable identities as tautological, 1=1. 162.158.142.100 04:09, 10 November 2018 (UTC)
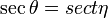 141.101.104.71 13:36, 10 November 2018 (UTC) AndreasH
141.101.104.71 13:36, 10 November 2018 (UTC) AndreasH
Am I the only one who saw t²n²a⁴ as "tuna"? 172.68.58.233 14:17, 10 November 2018 (UTC)
- Yes. 162.158.75.190 (talk) (please sign your comments with ~~~~)
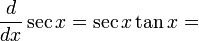 sex tanks. Probably not Douglas Hofstadter (talk) 21:36, 11 November 2018 (UTC)
sex tanks. Probably not Douglas Hofstadter (talk) 21:36, 11 November 2018 (UTC)
I thought "distance 2 banana" had to be a reference to QBasic's Gorillas game. "Enchant at target" could refer to the banana exploding when it hits something. mrpsbrk 162.158.123.91 (talk) (please sign your comments with ~~~~)
From when I saw 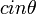 I knew the rest of the comic would be
I knew the rest of the comic would be  . Observer of the Absurd (talk) 13:28, 15 May 2019 (UTC)
. Observer of the Absurd (talk) 13:28, 15 May 2019 (UTC)
