3179: Fishing

Fishing

|< < Prev #3179 (December 10, 2025) Next > >|

Title text: 'That's definitely above the catch-and-release size minimum for planetesimals.' 'I'm going to throw it back anyway.'

|< < Prev Random Explanation Next > >|

Explanation

This is one of 54 incomplete explanations: This page was created BY A FISH WITH THE WEIGHT OF THE SUN. Don't remove this notice too soon. If you can fix this issue, edit the page!

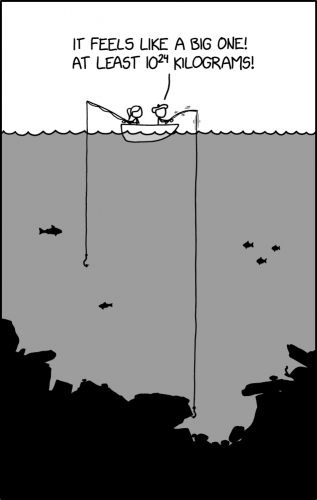
Ponytail and Beret Guy are fishing in the middle of a body of water, and Beret Guy has hooked a rock. He states that it must be 'at least 10²⁴ kilograms'. The joke here comes from the fact that Beret Guy has caught the Earth in its entirety, whose mass can be estimated at approximately 6.0x10²⁴ kilograms (~13.1x10²⁴ pounds at standard gravitational acceleration of the earth).

Catch-and-release sizes restrict what sizes of catch of various species can be kept, generally to protect stocks. There may be minimum sizes (to protect young fish and ensure that they can reach mature reproductive age) or maximum sizes (to protect existing breeding populations). Apparently, the Earth is too small to be kept, suggesting that it is considered an immature planet, and that it might be expected to grow to 'adult' planet size.

Transcript

This is one of 29 incomplete transcripts: Don't remove this notice too soon. If you can fix this issue, edit the page!

[Ponytail and Beret Guy are sitting on a boat in the ocean. Fish are seen swimming in the water. Megan has a fishing rod that is about halfway down to the ocean floor. Beret Guy's fishing hook is hooked onto the sea floor.]

Beret Guy: It feels like a big one! At least 10²⁴ kilograms!

  Add comment        Create topic (use sparingly)       Refresh 

Discussion

The tug on a fishing line would be measured in newtons, not kilograms. 76.187.17.7 04:30, 11 December 2025 (UTC)

It's at least a C+ 65.35.15.18 05:12, 11 December 2025 (UTC)

Yes, but he is not measuring the force, he is measuring the "weight" (mass) of the thing he thinks he hooked. (e.g. a 5 lb fish)2603:8000:5E00:2913:EE02:2D56:E960:2CDE 05:21, 11 December 2025 (UTC)

123:_Centrifugal_Force --88.65.244.212 20:18, 12 December 2025 (UTC)

He can't be weighing the object, it is under water. He can only be estimating its mass. BTW, the Earth is weightless, as it is in free fall. SDSpivey (talk) 15:02, 13 December 2025 (UTC)

YAY BERET GUY!Mathmaster (talk)

Beret Guy's estimate is, of course, absurd (or it would be for anyone else). His lifting capacity, the breaking points of his line and rod, the buoyancy of his boat and the force to break loose an individual piece of rock (the lowest of which would mark the upper bounds for his estimate) are (many) orders of magnitude lower than the force required to haul a 10^24 kg catch into the boat [citation needed, I guess] 627235 (talk) 11:42, 11 December 2025 (UTC)

He's not saying that he can reel it in, just estimating the size of the "fish" he's hooked. Barmar (talk) 14:57, 11 December 2025 (UTC)

When he pulls, there is a little bit of give (infinitesimal) as the planet moves - he might be sensing that and estimating based on it. Assuming you know the properties of the fishing line, like its stretch, and of the boat's surface area, buoyancy. I don't see why it wouldn't be possible to estimate given perfect knowledge of the water, boat, line, forces, etc, even if the Earth is much more massive than the boat being pulled downwards R128 (talk) 15:22, 11 December 2025 (UTC)

At that massive scale, wouldn’t the upper bound of weight he could detect the buoyancy of the boat - beyond that he is no longer pulling anything up, but pulling himself down - so that the resistance he feels is the buoyancy keeping the boat up? 71.17.36.59 16:18, 11 December 2025 (UTC)

You have to have a 'feel' for the potential elongation of the line (which depends a bit upon knowing how much you've deployed), the properties of the rod and (at least for fish, which weigh 'nothing', when they wish to be neutrally buoyant, but have a muscle-related resistive power and a degree of swim-bladder 'weight adjustment) the pseudo-weight that a given size of likely catch (of a likely species) fights against your line-tug with. You can get fooled that a static-snag is actively fighting you if you think you're only dealing with a fairly shallow fish when you've managed to snag onto something somewhat deeper so that the resonance of your attempts to pull give you the feeling of a reaction that's more just some kind of Young's Modulus/Hooke's Law artefact. It all feels completely different from a fish finally wrested entirely out of the water, and even allows a catch that's heavier than the eventual breaking-stress of your line (or weight+its effort to be greater than that) to be gradually played towards you while in the water, tiring it and bringing it into reach of your grasp/catch-net that will do the actual work of landing it.

Though, in this case, I think that Beret Guy knows how much line he is using/etc, and that he's hooked a planet (however that feels) rather than a more actively resisting (and tiring) seacreature. But by the very subtle reaction of the body to 'test tugs' (accounting for how this also moves the boat) he has correctly (within an order of magnitude!) assessed its 'dry mass'.

(A cynic might ask what other masses he might have caught, between Earth-sized and the next most massive mass that's hookable in this manner... a large part of the Titanic..? Having established that it 'tugs back' more than the latter, then Earth would be the only logical target to lead to such a 'logical guess' of mass. Though even establishing that it isn't a massive shipwreck probably needs extremely well tuned supersenses to rule out. So we can probably still consider it a preternatural Skill Of Beret Guy, even to do that.) 78.144.255.82 19:56, 11 December 2025 (UTC)

Planets don't have a catch size limit. By definition, a planet has cleared its neighborhood, meaning there's no need to maintain a breeding population. Now, dwarf planets and small solar system bodies are a different story, and the rules are rather strict. 209.188.63.98 19:08, 11 December 2025 (UTC)

I don't know whether you're supposed to throw planets back, if they're too small, but everybody knows that nobody tosses a dwarf... 78.144.255.82 22:11, 11 December 2025 (UTC)

Throwing planets back can have catastrophic effects on the local neighbourhood if you're not very careful about how you throw them back. 82.13.184.33 09:40, 12 December 2025 (UTC)

Beret Guy is surprisingly inaccurate on this one. You'd need to divide the actual weight of Earth by 6 to his estimated weight. --DollarStoreBa'al^Converse 19:23, 11 December 2025 (UTC)

I was wondering about that, and at first considered that he was either only referring to the mass of the Earth's crust (two orders of magnitude lighter), or including the mantle (factor or 4 heavier). Both options are way off. It's probably just a Fermi estimate. 2A02:590:1200:E001:EC09:A5D:4C27:42F3 21:32, 11 December 2025 (UTC)

He did say it was *at least* 10^24, which is not wrong... But you're right, he is off by quite a bit. R128 (talk) 13:44, 12 December 2025 (UTC)

I'd like to see you do any better. ;) 78.144.255.82 19:31, 12 December 2025 (UTC)

Just gave a rock a tug. Feels like six trillion trillion kilos, roughly. lmao R128 (talk) 20:03, 12 December 2025 (UTC)

Any reason to believe this is an ocean instead of a lake? I changed the transcript to make it more generic, but like "seafloor" better than "bottom," so would change it back if there is some reason to know it is an ocean. Bobthegoat123 (talk) 19:48, 11 December 2025 (UTC)

Has anyone considered that Beret Guy might be fishing on a different PLANET entirely? That would the explain the different mass he found. 47.152.132.12 19:03, 12 December 2025 (UTC)

What different mass? "At least 10²⁴ kilograms" is pretty darn close. And not even slightly excessive. Seems like a (very) good estimate of the Earth's mass to me. 78.144.255.82 19:29, 12 December 2025 (UTC)

The Earth's mass is 5.97 x 10²⁴ kilograms. The actual mass of the Earth is around 6 times 10²⁴. 47.152.132.12 03:25, 13 December 2025 (UTC)

Yes, pretty darned close, given the magnitude. Almost 97% the same, comparing ln/ln. 78.144.255.82 19:43, 13 December 2025 (UTC)
        Add comment