2407: Depth and Breadth
| Depth and Breadth |
 Title text: A death-first search is when you lose your keys and travel to the depths of hell to find them, and then if they're not there you start checking your coat pockets. |
Explanation
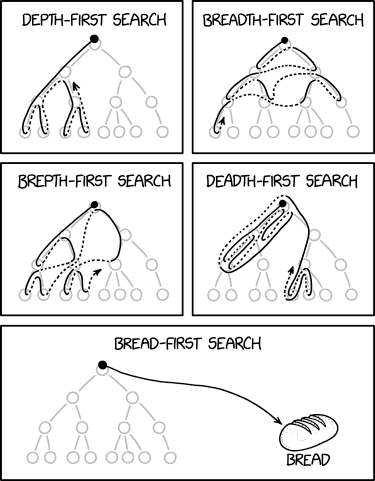
Tree structures are one of the most common data structures used in computer science. The common ways of enumerating items arranged in a tree is either depth-first, or breadth-first, which are depicted accurately in the comic. Randall humorously combines the words, to produce "brepth-first", "deadth-first", "bread-first", and "death-first" search algorithms.
Depth-first search explores down a full branch of the tree before working back to a higher level. This type of tree structure was already discussed as inefficient for human needs in 761: DFS. The "opposite" of this is breadth-first search, which explores each level of the tree at a time.
In the "brepth-first" algorithm, a depth-first and a breadth-first search are hybridized where the left-most node is visited more frequently than the right node, but the right node is still visited. This might be good for exploring data that is loosely but not strictly weighted to the left, or where data in deeper nodes needs some time to be loaded before it can be used. As implied by 761: DFS, this might be the best algorithm for a human to employ, where one can explore several topics briefly before deciding which one to explore more deeply, rather than blindly following the first rabbit hole to an absurd conclusion. Informed search algorithms like A* search, Beam search, and other Best-first search algorithms show this type of behavior by expanding the most promising node in the current set (under some appropriate metrics).
The nature of the "deadth-first" algorithm is unclear and inefficient, since it searches the same nodes multiple times before moving to an entirely different region of the tree. It might be useful in a context where examining nodes has some probability of returning a noisy or incorrect result, such as searching for small objects that may be overlooked.
The bread-first search is taken literally. Bread is searched for first. Since the computer user now has already met their want to find bread, the computer has no reason to explore the tree at all.[citation needed]
The title text introduces a "death-first" search, in which the user explores what it is like to be dead, before considering anything else. Specifically, the title text refers to hell, which calls to mind the adventures of Dante Alighieri in his Inferno, and is a less likely place for keys to be left than one's coat pockets [citation needed]. In 2021 (the year this comic was published) there are commemorations for the 700th anniversary of Dante's Death. These are expected to take place among the living only, and not in Hell.[citation needed] A much more pleasant death-first algorithm might be to skip hell and purgatory and search heaven first, perhaps multiple times (which in itself would be a use of the deadth-first approach).
Transcript
| |
This transcript is incomplete. Please help editing it! Thanks. |
- [Five panels, each containing identical copies of a rooted tree graph, grayed out in the background. The tree has a height of 3 and 15 nodes.]
- [In all five panels, a black twisty arrow in the foreground indicates the order in which nodes are traversed. The arrow does not complete the entire traversal but cuts off at some point. Backtracking is indicated with a dotted line.]
- [In the descriptions below, node 1 is the root, nodes 2 and 3 are its child nodes, nodes 4 and 5 are 2's child nodes, nodes 6 and 7 are 3's child nodes, nodes 8 and 9 are 4's child nodes, and so on up to node 15.]
- [Backtracking is omitted from the descriptions below, as they increased confusion when read.]
- Depth-first search
- [The arrow visits nodes 1, 2, 4, 8, 9, 5, 10, 11.]
- Breadth-first search
- [The arrow visits nodes 1, 2, 3, 4, 5, 7[sic], 6, 8.]
- Brepth-first search
- [The arrow visits nodes 1, 2, 4, 5, 8, 9, 3, 6, 10, 11.]
- Deadth-first search
- [The arrow visits nodes 1, 2, 4, 4, 2, 4, 3, 6, 12, 13, 12.]
- Bread-first search
- [The arrow starts at node 1, then immediately leaves the tree off to the right to point to a small loaf labeled "Bread".]
Discussion
Soldier loves bread-first search for obvious reasons.162.158.49.50 10:53, 5 January 2021 (UTC)
where did the quality go 172.69.34.24 19:34, 4 January 2021 (UTC)
- I noticed this too. As discussed at User:DgbrtBOT there are two sizes of each comic. The default (smaller) size of 2407 looks much worse than the original, which you can find at https://imgs.xkcd.com/comics/depth_and_breadth_2x.png I suggest we use the larger version for this comic. Alchemistmatt (talk) 20:18, 4 January 2021 (UTC)
- I tried to upload the higher quality PNG but I do not have permission; we'll have to wait for an editor to provide their opinion. Alchemistmatt (talk) 20:35, 4 January 2021 (UTC)
It would appear that the first version of the picture of this day's cartoon presents artifacts due to an unusual export method. The image seems to have been exported using the 'nearest neighbor' resampling method, which would explain the jaggy edges. Usually, the images appear to be exported using bilinear downsampling from an white-grey-black original, resulting in a published version with a larger color palette. 162.158.111.161 20:17, 4 January 2021 (UTC)
- Randall has uploaded a new image: [1], which I uploaded to explainxkcd. Natg19 (talk) 21:48, 4 January 2021 (UTC)
In the breadth-first, for the second node on the right, the right branch is searched first, while everywhere else, the left branch is. And in deadth-first, the nodes are searched multiple times (e.g. left-most node of layer 3 is search 3 times, assuming a search is at the end of a continuous line). Alternatively, maybe the search goes up first sometimes (it's not actually clear when a node is being looked at), but that doesn't explain the order of the left-most node of layer 2. 172.68.142.201 22:15, 4 January 2021 (UTC)
- I noticed that. With perhaps two reasons: 1) aesthetics - drawn to go to nodes .2, .2.1, (.2), .2.2, then .1.1.1 (via .1.1, crossing .2.1, .1.2) would look a bit worse than this (crossing just .1.2); or 2) there's no absolute sorting order vs choice, it's just chance (or aesthetic choice) that .1s take priority over .2s in every other case - 3 out of the four choices is well within explorative chance.
- I favour the latter (with maybe an aesthetic bias) as often when I run a tree-searching algorithm I like to randomly splice the next option out of the list of options (rather than run from first to last or last to first) where I am not aware of any advantageous link (maybe in ruling out 'dead' branches early to prune off useless branches early) and thus whatever natural sort-order the structure imposes would create biases.
- Alternately, if continued it would definitely prioritise .2s down every .2(-dominant) branch, for a nicely symmetric 'wide-breadth first' pattern (.2.2.2 over .2.2.1, etc) for a pattern only visible once continued beyond the step currently shown. The root choice cannot be anything other than symmetry-breaking, but could as easily be a coinflip. 141.101.98.68 00:32, 5 January 2021 (UTC)
- If you look at the bottom row you can see that these are not binary trees but rather arbitrary graphs (one node has 3 children). So assuming arbitrary order when enumerating children is reasonable. Quantum7 (talk) 08:46, 8 January 2021 (UTC)
The top two drawings for "depth" and "breadth" are legitimate methods of listing out a tree structure. The next two drawings substitute the "d" and "br" from "depth" and "breadth" to get "brepth" and "deadth". The fifth drawing removes the "th" from "breadth" to get "bread". And the title text substitutes the "p" from "depth" with an "a" to get "death". Rtanenbaum (talk) 22:32, 4 January 2021 (UTC)
After the bread-first search, the next logical variant is the breakfast search! PotatoGod (talk) 04:58, 5 January 2021 (UTC)
I associated this comic with the way (non native english speakers like myself) tend to pronounce words like depth and breadth, especially during discussions about which tree traversal strategy to use. Then, using a term like breadth-first can easily degrade to dep-first and bread-first (skipping the harder-to-pronounce 'th'). So maybe add this as a possible background? 162.158.159.50 12:42, 5 January 2021 (UTC)
Somebody erased my commentary on deadth-first and hell regarding AI problems. These problems are real and people have experienced them firsthand. I notice the changes added in some heaven-references. I'm happy to add a much more pro-AI slant to the commentary; obviously AI makes lots of heaven, this is just not the _only_ thing that happens as people explore it. I don't think it's appropriate to leave information out, calling the brepth-first search more adaptive than the deadth-first search. It's pretty obvious from the dotted lines that the deadth-first search is adaptively considering its branches, and not revisiting nodes. I don't have the energy atm to start an actual edit war and add my information back in. 108.162.219.74 18:07, 6 January 2021 (UTC) EDIT: on closer review I see both exploration strategies have pretty deterministic behavior, and are quite poorly described by the commentary.
I went ahead and tried to implement this on NPM https://www.npmjs.com/package/bread-first-search 162.158.74.149 19:30, 6 January 2021 (UTC)
Can anyone write pseudocode for the brepth searches? I feel like there is a certain logic to it, but I'm unable to clearly articulate the recursion. Pseudocode seems infeasible for deadth-first, as the multiple visits make it fairly incomprehensible. Quantum7 (talk) 08:44, 8 January 2021 (UTC)
172.68.132.19 22:17, 8 January 2021 (UTC)Am I the only person that sees the deadth first search is a raptor?
There is no description of the breadth-first algorithm. Also while the third paragraph talks about brebth-first image, the reference to 761: DFS which was added by BlackHat is actually talking about breadth-first and not brebth-first. 172.68.63.137 18:37, 11 January 2021 (UTC)
now randall should also implement a toast search! An user who has no account yet (talk) 22:37, 2 September 2023 (UTC)
