2059: Modified Bayes' Theorem
| Modified Bayes' Theorem |
 Title text: Don't forget to add another term for "probability that the Modified Bayes' Theorem is correct." |
Explanation[edit]
Bayes' Theorem is an equation in statistics that gives the probability of a given hypothesis accounting not only for a single experiment or observation but also for your existing knowledge about the hypothesis, i.e. its prior probability. Randall's modified form of the equation also purports to account for the probability that you are indeed applying Bayes' Theorem itself correctly by including that as a term in the equation.
Bayes' theorem is:
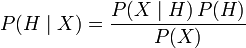
- P(H | X) is the probability that H, the hypothesis, is true given observation X. This is called the posterior probability.
- P(X | H) is the probability that observation X will appear given the truth of hypothesis H. This term is often called the likelihood.
- P(H) is the probability that hypothesis H is true before any observations. This is called the prior, or belief.
- P(X) is the probability of the observation X regardless of any hypothesis might have produced it. This term is called the marginal likelihood.
The purpose of Bayesian inference is to discover something we want to know (how likely is it that our explanation is correct given the evidence we've seen) by mathematically expressing it in terms of things we can find out: how likely are our observations, how likely is our hypothesis a priori, and how likely are we to see the observations we've seen assuming our hypothesis is true. A Bayesian learning system will iterate over available observations, each time using the likelihood of new observations to update its priors (beliefs) with the hope that, after seeing enough data points, the prior and posterior will converge to a single model.
The probability always has a value between zero and one, the latter value represents a 100% probability. Both extremes would be:
- If P(C)=1 the modified theorem reverts to the original Bayes' theorem (which makes sense, as a probability one would mean certainty that you are using Bayes' theorem correctly).
- If P(C)=0 the modified theorem becomes P(H | X) = P(H), which says that the belief in your hypothesis is not affected by the result of the observation.
It is a linear-interpolated weighted average of the belief from before the calculation and the belief after applying the theorem correctly. This goes smoothly from not believing the calculation at all up to be fully convinced to it.
Bayesian statistics is often contrasted with "frequentist" statistics. For a frequentist, probability is defined as the limit of the relative frequency after a large number of trials. So to a frequentist the notion of "Probability that you are using Bayesian Statistics correctly" is meaningless: One cannot do repeated trials, even in principle. A Bayesian considers probability to be a quantification of personal belief, and so concepts such as "Probability that you are using Bayesian Statistics correctly" is meaningful. However since the value of such subjective prior probablities cannot be independently determined, the value of P(H|X) cannot be objectively found.
The title text suggests that an additional term should be added for the probability that the Modified Bayes Theorem is correct. But that's this equation, so it would make the formula self-referential, unless we call the result the Modified Modified Bayes Theorem. It could also result in an infinite regress -- needing another term for the probability that the version with the probability added is correct, and another term for that version, and so on. If the modifications have a limit, then a Modifiedω Bayes Theorem would be the result, but then another term for whether it's correct is needed, leading to the Modifiedω+1 Bayes Theorem, and so on through every ordinal number.
Modified theories are often suggested in science when the measurements doesn't fit the original theory. An example is the Modified Newtonian dynamics theory, among many others, in which some physicists try to explain dark matter with not much success.
Transcript[edit]
- [The comic shows a formula with a header in gray on top:]
- Modified Bayes' theorem:
- [The formula:]
- P(H|X) = P(H) × (1 + P(C) × ( P(X|H)/P(X) - 1 ))
- [Variables and functions are described also in gray:]
- H: Hypothesis
- X: Observation
- P(H): Prior probability that H is true
- P(X): Prior probability of observing X
- P(C): Probability that you're using Bayesian statistics correctly
Discussion
Right now the layout is awful:
- "If
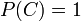 the..."
the..." - should look like this:
- "If P(C)=1 the..."
But there is more wrong right now. Look at a typical Wikipedia article, the Math-extension should be used for formulas but not in the floating text. --Dgbrt (talk) 20:03, 15 October 2018 (UTC)
- Credit for a good explanation though. It made perfect sense to me, even though I didn't understand it. 162.158.167.42 04:14, 16 October 2018 (UTC)
I removed this, because it makes no sense:
- As an equation, the rewritten form makes no sense.
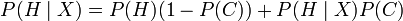 is strangely self-referential and reduces to the piecewise equation
is strangely self-referential and reduces to the piecewise equation 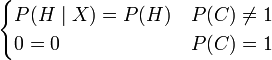 . However, the Modified Bayes Theorem includes an extra variable not listed in the conditioning, so a person with an AI background might understand that Randal was trying to write an expression for updating
. However, the Modified Bayes Theorem includes an extra variable not listed in the conditioning, so a person with an AI background might understand that Randal was trying to write an expression for updating 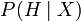 with knowledge of
with knowledge of 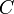 i.e.
i.e. 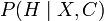 , the belief in the hypothesis given the observation
, the belief in the hypothesis given the observation 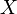 and the confidence that you were applying Bayes' theorem correctly
and the confidence that you were applying Bayes' theorem correctly 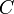 , for which the expression
, for which the expression 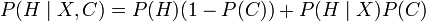 makes some intuitive sense.
makes some intuitive sense.
Between removing it and posting here, I think that I've figured out what it's saying. But it comes down to criticizing a mistake made in an earlier edit by the same editor, so I'll just fix that mistake instead.
—TobyBartels (talk) 13:03, 16 October 2018 (UTC)
What about examples of correct and incorrect use of Bayes' Theorem? I don't feel equal to executing that, but DNA evidence in a criminal case could be illuminating. As a sketch, it may show that of 7 billion people alive today, the blood at the scene came from any one of just 10,000 people of which the accused is one. Interesting, but not absolute. At least 9,999 of the 10,000 are innocent. Probability of mistake or malfeasance by the testing laboratory also needs to be considered. Then there's sports drug testing, disease screening with imperfect tests and rare true positives, etc. [email protected] 141.101.76.82 09:42, 17 October 2018 (UTC)
Where is the next comic button for this page? IYN (talk) 15:46, 17 October 2018 (UTC)
- Please be patient for that button, it always appears a little bit late since a few days ago when a new comic is out. Right now you always can click the Latest comic link at the menu. I'm aware of this minor issue. --Dgbrt (talk) 20:16, 17 October 2018 (UTC)
 Add comment
Add comment
