216: Romantic Drama Equation
| Romantic Drama Equation |
 Title text: Real-life prospective-pairing curves over things like age can get depressing. |
Explanation[edit]
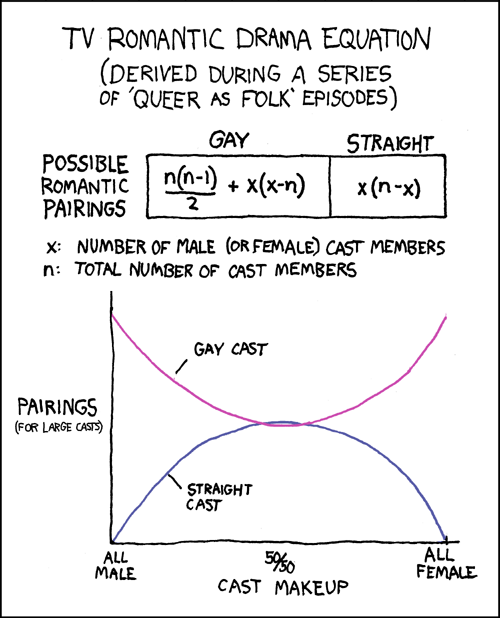
In a group of n people, such as the cast of a TV romantic drama like Queer as Folk, the number of possible different pairs of people is n(n-1)/2. A romantic drama will often consider, over time, many possible romantic pairs of its cast members, even seeming to test the limit of how many pairs are possible. Through an austerely binaristic lens, this comic explores the implication of sex and sexual orientation in characterizing the possible pairs.
If everyone in the group is male or female, then each pair could be classified as gay or straight. The formulas in the comic give how many of the possible pairs are gay and how many are straight, as a function of the total number of people and how many are male (or, equivalently, how many are female.) For example, of the 9 principal cast of Firefly, 5 are men and 4 are women. With n=9 and x=5, we have 16 possible gay pairs and 20 possible straight pairs.
A graph shows how the relative number of males and females affects the number of gay pairs and straight pairs. When the group is all male (or all female), all of the possible pairs are gay, but as the minority sex's number is increased, more of the pairs are straight. When the group is half male and half female, the number of straight pairs is maximized, and straight pairs slightly outnumber gay pairs. The curves are labeled "gay cast" and "straight cast", perhaps implying that a "gay cast" would consider only gay pairs, and a "straight cast" would consider only straight pairs.
There is a note that the graph describes large casts. Because all the quantities involved are discrete, for a small [n] there are only a few points to plot on the graph, and the smooth, continuous curves seen in the comic are less recognizable.
The title-text mentions that Randall made a graph of his prospective dating pool over time and was depressed by the results. As he gets older, his dating pool gets smaller: fewer people his age are single. But as Randall later shows in 314: Dating Pools, age is not the problem--he is!
Formulas[edit]
The formulas may be derived as follows:
Each straight pair needs to include one of the x males and one of the (n-x) females, so there are x(n-x) possible ways of combining one of each. E.g., if there are n=5 people, of whom x=2 are male, then there will be 3 possible pairings involving the first male, and 3 possible pairings involving the second, yielding 2(5-2)=6 possible pairs.
Wolfram|Alpha: x*(n-x)
Each gay pair needs to include either two males or two females. To choose two males, we can start with any of the x males and choose any of the (x-1) remaining males. However, that counts each possible pair twice. E.g., Adam&Steve got counted when we chose Adam first and Steve second, and again when we chose Steve first and Adam second. To avoid double-counting the pairs, we therefore need to divide the product by 2. So there are x(x-1)/2 possible pairs of two males. Similarly, there are (n-x)(n-x-1)/2 possible pairings of two females. Summing these, we get the total number of possible gay pairs as [x^2 - x + n^2 - nx - n - xn + x^2 + x]/2. That simplifies to [n^2 - n + 2 x^2 - 2 xn]/2. The left two terms can be combined together as n(n-1) and the right two terms can be combined together as -2x(n-x) or 2x(x-n) [which is negative, because x-n<0]. Since the sum of these terms was divided by 2, we get that the total number of possible gay pairs is n(n-1)/2 - x(n-x), or n(n-1)/2 + x(x-n), which is what the cartoon says.
Wolfram|Alpha: n*(n-1)/2+x*(x-n)
Desmos: https://www.desmos.com/3d/j0sgfhbcci
Transcript[edit]
- TV Romantic Drama Equation (Derived during a series of 'Queer as Folk' episodes)
- [A table shows equations for possible romantic pairings in a TV show. The equation under "gay" is n(n-1) 2+x(x-n); the equation under "straight" is x(n-x).]
- x: Number of male (or female) cast members.
- n: total number of cast members.
- [A graph plots pairings (for large casts) against cast makeup. Each of the above equations forms a curve. "Gay cast" starts high for an all male cast, dips down at 50/50 cast makeup, and then rises again for all female. "Straight cast" starts at zero for an all male cast, peaks at 50/50 cast makeup, and then drops to zero again for an all female cast. The two curves intersect at two points close to the middle.]
Discussion
This can't be right, even at 50/50, the number of gay pairings far outnumbers the number of straight pairings.80.235.105.134 20:10, 28 February 2013 (UTC) Moved from article page
- Not quite. Consider a cast of 4 with 2 male (A, B) and 2 female (C, D). Possible gay pairings - 2 (A-B and C-D). Possible straight pairings - 4 (A-C, A-D, B-C, B-D) 122.200.61.203 (talk) (please sign your comments with ~~~~)
- He says for large casts. For 2000 cast members, with 1000 of each gender, the gay couplings comes out at 999,000 and straight at 1,000,000. Presumably this is the small cross over the diagram alludes to. If you substitute x = n/2 into the equations, then you get (n^2-2n)/4 for the gay combinations and n^2/4 for the straight combinations, so for gender balanced cast size of n, the straight combinations outnumber the gay by n/2 141.101.98.229 (talk) (please sign your comments with ~~~~)
- The intuitive explanation for this is that if there are equally many men and women (i.e., x = n/2), each individual can pair with (n/2 - 1) others of the same gender, but with n/2 of the opposite gender. So each individual has 1 more pairing with the opposite gender than with the same gender. Taken across the population, that leads to a difference of n/2. 172.71.126.145 10:13, 11 March 2024 (UTC)
There is a typo in his formula for gay casts. The + should be a -. 199.27.128.159 (talk) (please sign your comments with ~~~~) No, he's right. Notice the x-n term. x<n, so x-n is negative.108.162.215.61 03:14, 2 March 2014 (UTC)
This also the small implication that "Queer as Folk" was so dull that Randall produced this equation to occupy his mind during it. I often find my mind wandering while sat watching soaps with my other half. Drmouse (talk) 14:20, 3 January 2014 (UTC)
The first equation can also be understood more simply as the total number of possible pairings, minus the number of straight ones. 162.158.23.191 (talk) (please sign your comments with ~~~~)
- Good point! I wonder where exactly that small crossover region should be. n(n-1)/2 - x(n-x) = x(n-x) so n(n-1)/2 = 2x(n-x) so n(n-1) = 4x(n-x). Hm, he said for large casts, so I suppose Randall's making approximations based on the limit. As n -> infinity, n(n-1) -> n^2, and as x -> n/2, 4x(n-x) -> 2 n(n/2) which is also n^2. So it makes sense that the crossover region gets closer to just being one point at n/2. But can we calculate an exact trend? n(n-1)=4nx-x^2, so x^2-4nx+n(n-1)=0, so x=[4nx±sqrt(16-4(n)(n-1))]/2, so x(1-2n)=x-2nx=±sqrt[16-4(n)(n-1)]/2=±sqrt[4-n(n-1)], so x=±sqrt[4-n(n-1)]/(1-2n). Also, that can't possibly be right because it would give a negative answer but whatever, it's late, I think I did the approximated math right so that's good enough 172.68.78.100 05:53, 21 June 2017 (UTC)
I think all genders being constant isn't really an assumption of the graph. Obviously the graph only works for a single moment in time in a TV show, since the cast changes over time with the plot of the show (such as when people die in the show). The graph already needs to be re-drawn every time someone enters or leaves the cast. For the data we're tracking, a sex change operation is the same as, for example, a man leaving the show and a woman subsequently entering it. Sure, you could then also say that the cast being constant is an assumption of the graph, but that's not really accurate either. The graph simply doesn't observe the passage of time. You'd have to add a time axis for that, making the graph three-dimensional. 172.68.26.251 04:15, 21 March 2017 (UTC)
I think a better way to explain the gay pairing equation would be to look at it like this: n(n-1)/2 are all possible pairings, since you take each person(n), pair them with everyone except themselves(multiply by n-1) and then divide by 2 to eliminate pairing the same people twice. Then substract x(n-x) which is the equation for all straight pairings. - x(n-x)=x(x-n), hence the second part of this equation.(Hope I'm editing correctly)
It actually comes out that if each individual's gender is chosen randomly, the expected value for straight casts and for gay casts is the same (not too hard to prove via induction).