2294: Coronavirus Charts
| Coronavirus Charts |
 Title text: Adding data for South Korea but with their cases scaled to match the population of Japan and the land area of Australia, and vice versa. |
Explanation[edit]
This comic is the 19th comic in a row (not counting the April Fools' Day comic 2288: Collector's Edition and the previous tribute comic) in a series of comics related to the COVID-19 pandemic.
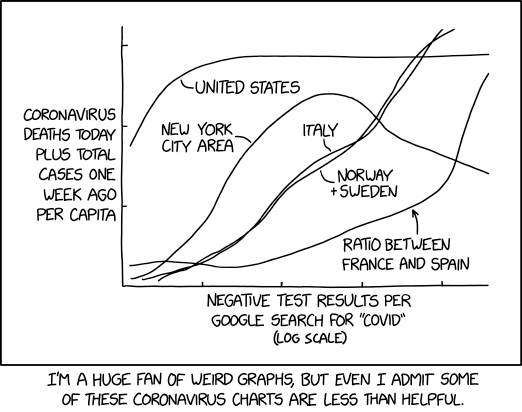
During the current outbreak of COVID-19, there have been many graphs used by health officials and others to show trends in infection and death rates. Their x-axis is usually time. The curves might represent different countries or different mitigation strategies. But health officials and media have struggled to decide what to put on the y-axis. Because testing strategies and reporting are so variable across even small regions, their data does not reflect comparable guesses at the true number of cases. So they produce graphs of confirmed cases, confirmed plus suspected cases, deaths, hospitalizations, any of the above per capita, day-to-day changes in any of the above, and share of test results that are positive for different areas of New York.
However, this graph, while sharing similarities with actual data and graphs, is completely useless. This is due to the bizarre data-points being used, as well as the unhelpful graph axes. The caption of the comic notes as much, perhaps indicating that this comic is intended to satirize the useful, but exceptionally detailed graphs that are currently in use. Some of these graphs have a semilog scale, like this graph - but generally the y-axis is the log scale and the x-axis is not. Sometimes the other graphs compare things of vastly different sizes - as demonstrated by showing both the USA and New York. Sometimes they scale the data to population, as referenced by the title text.
In addition, the selection of geographic areas used here is incomprehensible. Two of the lines represent countries (USA and Italy), and another represents part of one of those countries (New York City area). The New York City area may have been chosen because it has a very large number of cases, more than some countries. However, a fourth line combines Norway and Sweden -- two countries which are culturally, economically, and geographically similar but have imposed very different strategies regarding closing businesses and schools. Combining Norway and Sweden obscures any differences attributable to their different policies regarding the virus. A fifth line represents not a geographical area but the ratio between France and Spain, making an already meaningless graph even less comprehensible.
The title text adds a further ambiguity: Usually, there are only two items being compared in a "vice versa" (e.g. "Would you rather have live in a city with the land size of San Francisco and the population density of Tokyo, or vice versa?" when comparing two other cities with those measurements); here there are three, leading to either ambiguity (possibly two South Korea lines, each based on one of two complementary sets of cross-demographic refactoring), or six lines being embodied in that "vice versa".
Other metrics used
X-axis:
- Negative test results: Negative test results would refer to people who were tested for COVID-19, but who do not have the disease (or were not able to confirm having the disease). If there are any places reluctant to test, in order to artificially suppress the unpopular number of positives, this measure would similarly be unreasonably low. It might therefore be an important key measure, used as just one component of a meta-measurement, to regrade or even highlight such practices. At least until the figures are freshly massaged by instead overtesting people with a low probability of being infected.
- per Google search for "COVID": Meanwhile, Google search results for "COVID" are search hits for that word. There is no relation between these two, and furthermore, it does not make sense for this to be graphed on a logarithmic scale.
- As mentioned above, the x-axis for most charts is time, as it is valuable to know how the virus or deaths are spreading over time. Negative test results should grow over time, but may not grow uniformly depending on availability of tests, and some may later be invalidated as testing methodologies are refined. Given that and depending on the trends in Google searches for COVID, it's entirely possible for multiple points in time to map to the same value of x (although none of the curves shown here do, Scenario 4 from 2289: Scenario 4 did).
Y-axis:
- Coronavirus deaths today: Deaths from the coronavirus "today" are constantly reported by the media, and could be a helpful metric in seeing whether the virus is spreading or not, if deaths "today" are compared to deaths yesterday and previous days.
- Total cases one week ago: This is a much larger number than deaths and will completely dominate the sum. Cases one week ago might have some predictive value for deaths today or in the near future, but adding them together double-counts many cases.
- Per capita: This is a measure of the amount per person, and is useful for averaging out numbers based on population size. For example, the United States have the most publicly-reported COVID-19 cases and deaths, but also has the third-largest population of all countries, so using per capita numbers tells a different story.
Title text: While adding data for South Korea might be helpful (as it shows an Asian country, compared to just Europe and the US), it is only logical to scale the data to the population of another country (e.g. Japan) if you're actually comparing the two countries (i.e. does Japan have more or fewer cases per capita than South Korea). Scaling cases based on land area is much less useful; it's true that countries with lots of land area, like Australia, do have lower population densities, which affects the spread of disease, but most of the people in Australia live in higher-density cities on the coast, so the actual change is not that great.
Transcript[edit]
[A graph is drawn.]
- [A curve labeled "United States" starts about halfway up the vertical axis, rises almost to the top, and then levels off about a third of the way along the horizontal axis.]
- [4 other curves are also shown, labeled "New York City area", "Italy", "Norway + Sweden" and "Ratio between France and Spain".]
- Y-axis label: Coronavirus deaths today plus total cases one week ago per capita
- X-axis label: Negative test results per Google search for "COVID" (log scale)
- Caption: I'm a huge fan of weird graphs, but even I admit some of these coronavirus charts are less than helpful.
Discussion
It must be because there aren't any numbers along the axes 172.69.34.104 23:53, 15 April 2020 (UTC)
I want to know if this is a random sketch with silly labels, or if Randall looked up actual data to plot it. It seems to be a combination of 4 metrics which might be reported somewhere (search popularity, death rate, total reported cases, and number of tests performed). I suspect there aren't many countries/regions for which all 4 are available, but it's conceivable that someone's published enough stats to draw this crazy plot. ¬Angel (talk) 01:39, 16 April 2020 (UTC)
- What would negative results in a google search be? How do you make them a graph axis? I think its just random labels on graphs. --Lupo (talk) 05:12, 16 April 2020 (UTC)
- It doesn't say negative test results for a google search. It's the number of people who've tested negative for the disease, divided by the number of people who've searched google for it. I'm moderately surprised that nobody's yet started a list of links to various data soources that could be used to plot this graph. Does Google provide per-country search frequencies? ¬Angel (talk) 09:34, 16 April 2020 (UTC)
- Google Trends is always normalized so that the data returned is in [0, 100], and denormalizing out of relative values back to raw numbers is almost impossible. The best you can do is get a unitless proportion by comparing to a second search term chosen as one which doesn't vary much over time. 172.68.142.203 10:54, 16 April 2020 (UTC)
- From the docs, looks like that data is simply scaled. "A value of 50 means that the term is half as popular [as its most popular day]". Using that 0-100 number as if it were an actual number of people should give the same graph, just with the units on the X-axis offset by some value. Positioning the graphs relative to each other would be harder, as the "Interest by region" chart doesn't follow the same rules; we're lacking good data for the ratio between one country and another. Angel (talk) 13:48, 16 April 2020 (UTC)
- Google Trends is always normalized so that the data returned is in [0, 100], and denormalizing out of relative values back to raw numbers is almost impossible. The best you can do is get a unitless proportion by comparing to a second search term chosen as one which doesn't vary much over time. 172.68.142.203 10:54, 16 April 2020 (UTC)
- It doesn't say negative test results for a google search. It's the number of people who've tested negative for the disease, divided by the number of people who've searched google for it. I'm moderately surprised that nobody's yet started a list of links to various data soources that could be used to plot this graph. Does Google provide per-country search frequencies? ¬Angel (talk) 09:34, 16 April 2020 (UTC)
Is the y-axis (death_today + cases_aweekago)/capita or death_today + (cases_aweekago/capita)? This would hugely effect the weighting of the two terms. (Parentheses in second interpretation are for clarity only, I know they change nothing mathematically.) 172.69.54.9 09:03, 16 April 2020 (UTC)
- Perhaps it is intentionally ambiguous to support the main point about bad charts. 172.68.142.203 10:54, 16 April 2020 (UTC)
- I assumed the latter; but the page here seems to assume the former. Either way, one of the results will dwarf the other. Angel (talk) 13:48, 16 April 2020 (UTC)
The 19th COVID19 comic... :-) almost in a row. --Kynde (talk) 12:40, 16 April 2020 (UTC)
I tried my hand at graphing the data for the United States, in this spreadsheet here: [1]. If anybody is motivated enough to add data from other countries, go ahead. As it is, this data doesn't really look anything like what Randall graphed, making me think that he just made up the lines. 172.68.174.82 16:42, 16 April 2020 (UTC)
- OH NO! 172.68.143.96 18:43, 16 April 2020 (UTC)
- Well, since the x axis doesn't graph time, there's no reason for the trend lines to be functions of x— he just chose to draw them that way. Both x and y are independent functions of t. 172.68.174.70 19:11, 16 April 2020 (UTC)
I suddenly wondered if the graph means negative test results to date; or the new ones returned today. Same for the Google results, I guess. The Y-axis explicitly says it's talking about the total number of cases and today's death count, but the X-axis doesn't say for either of its values. And then that gave me the idea that "total" on the Y axis might actually mean "worldwide". So now I'm reading the Y-axis label as being (today's deaths in $country)+(worldwide infection count/population of $country). Maybe that makes the graph more useful. Angel (talk) 22:36, 16 April 2020 (UTC)
So did this comic not come out on 4/15 or is that just me? It seemed like all of yesterday was still the Conway Memorial comic. 172.69.63.167 22:48, 16 April 2020 (UTC) Acolyte
- i thought so too! is this the first time in ages that randall missed a day? maybe someone wants to add this to a trivia section. -- //gir.st/ (talk) 23:01, 16 April 2020 (UTC)
- I saw this comic on 4/15 (late in the afternoon/early evening PDT). According to Randall here, it was posted on 4/15. 172.69.34.104 00:19, 17 April 2020 (UTC)
- looking at the first capture in the internet archive (https://web.archive.org/web/20200415230401/https://xkcd.com/2294/), it was indeed posted on the 15th -- albeit at 23:04:01. -- //gir.st/ (talk) 13:53, 17 April 2020 (UTC)
- I saw this comic on 4/15 (late in the afternoon/early evening PDT). According to Randall here, it was posted on 4/15. 172.69.34.104 00:19, 17 April 2020 (UTC)
I've removed the remark that logarithmic scale axes "would not have evenly spaced ticks as shown", as it is incorrect. when the marks are 10, 100, 1000, ... the marks are evenly spaced. -- //gir.st/ (talk) 23:00, 16 April 2020 (UTC)
For those of you interested in the difficulties experienced by epidemiology under the embarrassment of riches allowed by contemporary big data, please see this working draft on the sufficiency of testing. 172.69.22.146 23:59, 16 April 2020 (UTC)
There's a graph from an economist at the Cleveland Federal Reserve Bank that may have been an inspiration for this comic--it has log scales and a difficult to decipher X-axis that is only vaguely time-like. Also discussion here.
--DanR (talk) 15:13, 17 April 2020 (UTC)