2671: Rotation
| Rotation |
 Title text: It's okay, we can just feed the one-pixel image into an AI upscaler and recover the original image, or at least one that's just as cool. |
Explanation[edit]
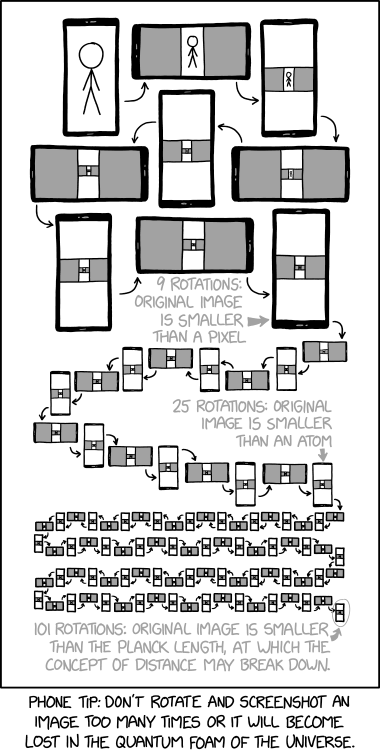
This is another one of Randall's Tips, this time a phone tip. This tip claims that rotating a phone and taking a screenshot too many times will cause an image to disappear into nothingness and warns the user against doing so. The camera and the display both have limited resolutions, so the detail of the original screenshot at the center of the image will be reduced as it approaches the range of a few pixels, hence the original image will be lost before it reaches the sub-pixel range. This is funny because the default resolution of contemporary camera phones can be too large to meet size requirements for e.g. mobile phone Multimedia Messaging Service, web file uploads, or email attachments, so one or two steps of this awkward procedure are sometimes necessary. Other comics such as 878: Model Rail also use recursion as limits.
For a fuller explanation of the concepts involved, including Planck units, often associated with the topological quantum foam of string theory, see this CGP Grey video. For an explanation of topological string theory, see 2658: Coffee Cup Holes. See also 1683: Digital Data for an analogous image processing concept.
The title text refers to producing photographically likely higher resolution images from lower resolutions, an active area of current research.[1] Because reducing the resolution of an image is a lossy process, results obtained through such processes will not be able to perfectly recreate the original. Machine learning can be used to calculate how images of known photographic subjects (or e.g. anime-style art, in the case of waifu2x) behave under certain types of noise or reduction in size, so that images of those kinds can be upscaled in a way that, if not perfectly recreating the original, at least is a faithful representation, but when the image is scaled all the way down to one pixel, everything except a small amount of data about the image's overall color is lost, making reconstructing the original image impossible. Randall disclaims that, because the AI upscaling is based on ingesting a large corpus of human-made art (with subjects that we find 'interesting' or at least meaningful being predominantly represented), the AI will produce an image that is at least as cool as the original image was, and in fact some image generation AIs actually work on a similar principle — for example, "reverse diffusion" AIs are trained by teaching them to reconstruct images from noise, at which they can produce entirely new images by being fed actual noise. He could also be making a pun on color temperature, which the upscaler will be able to match to the original image. The "enhance button" for upscaling images is a common trope in movies and television, especially in crime and science fiction stories.
Mathematical corner[edit]
The scale reduction caused by a rotation can be approximated. If a is the width of the picture and b its height, the reduction is x=a/b, the aspect ratio of the picture rectangle. As can be seen in the comic, the first rotation leaves two gray areas on each side of the picture that are roughly square. The width of the reduced picture is x*a = a²/b. Each gray area is a (high) by (b-x*a)/2 (wide). This is roughly square, but will not be exactly square unless
- b = 2a + x*a and since x=a/b, dividing by b we obtain 1 = 2x + x².
This is a quadratic equation, whose only positive solution is √2-1 ≈ 0.414
Returning to the general problem: the reduction is geometric, so that after nine rotations, the picture will be reduced by a factor of x⁹. Since this is "smaller than a pixel", the original screen resolution is fewer than (1/x)⁹ pixels. It is not stated whether it is the width, height, or area of the original picture that have been reduced to "smaller than a pixel".
25 rotations reduces a lot further and logarithms are useful to compute that. Let L be log(a/b), a negative number since a/b is less than 1. If the original screen is 10cm wide, its reduced picture will be x^25 times smaller in width. The comic tells us that the picture is now "smaller than an atom" (typically 10^-10m). If referring to the width, then 25L is less than about -9.0 using base-10 logarithms.
After 101 rotations, the reduction will be x^101, and the picture is now "smaller than the Planck length". The log of the Planck length is about -34.8, so 101L is less than -33.8.
Significantly we know that 100 rotations was not enough, so 100L is greater than -33.8. If we split the difference and say that 100.5L is equal to -33.8, we get an aspect ratio a/b just about 0.461. Multiple popular phone sizes are within the range, including the iPhone X or XS both with an aspect ratio of 1125/2436 ~ 0.4618.
Transcript[edit]
- [A phone in portrait orientation shows an image of Cueball standing. It is then rotated, showing the image smaller with bars in landscape orientation, then the next phone is in portrait showing the entire screen of the previous rotated sideways, shrinking it every time. An arrow points from each phone to the phone with the next smaller image, until the last one. The labels, at the 9th, 25th, and 101st rotation, show the decreasing size of the original image as it goes through successive rotations.]
- [Labels:]
- 9 rotations: original image is smaller than a pixel.
- 25 rotations: original image is smaller than an atom.
- 101 rotations: original image is smaller than the Planck length, at which the concept of distance may break down.
- [Bottom caption:]
- Phone tip: don't rotate and screenshot an image too many times or it will become lost in the quantum foam of the universe.
Discussion
For extra credit: Waht is the resolution of the phone screen? 172.71.94.135 18:59, 12 September 2022 (UTC)
- From the image you can assume an 9/20 aspect ratio. Assuming each rotation reduces the image dimensions by that fraction after 9 rotations the dimensions would be reduced 1322 times so the resolution would be something between 1322x595 pixels (anything less than that would made it require 8 rotations or less) to 2935x1321 pixels (anything beyond that would require 10 rotations or more). 1600x720 or 2400x1080 maybe? Applying the same formula for the phone width and assuming atoms are typically around 100 picometers across then the phone width is close to 4.67 cm, too small, but maybe that's because rounding. In the other hand that formula does not work with Planck length at all: using it the phone width would be 1.69 meters. If you assume a width of 7 cm and 97 rotations you get pretty close to Planck length, but the comic says 101, not 97. Something is wrong with my calculations, I don't know what. 162.158.63.160 21:03, 12 September 2022 (UTC)
- I took almost the reverse approach. Estimate phone height is 0.2 metres, Planck length is 1.6e-35 metres, ratio is 1.25e34, then take the 101th root. That would give about 2.176 as the reduction factor, which is also the screen aspect ratio. Then ask, "how far off might this be?" I assumed the 101th reduction is just barely smaller than the Planck length, it could be almost another reduction and still work. In other words, the aspect ratio is constrained to be between the 101th root and the 102nd root of the screen height in Planck units. With a 20 cm high screen, that puts the aspect ratio between 2.159 and 2.176 -- so the 9:20 aspect ratio (2.222) is completely ruled out. However
all thelatest iPhone sizes work just fine: 1792/828=2.164,2436/1125=2.165, 2688/1242=2.164, 2436/1125=2.165. I'll just guess that Randall has one of those. Mrob27 (talk) 06:41, 13 September 2022 (UTC) - Adding: I forgot to apply your method to constrain the width in pixels. 1125 and 1242 is ruled out because they are bigger than 2.159^9. In fact all the phone dimensions in that list I linked are ruled out except one: iPhone XR, 828x1792 pixels. Mrob27 (talk) 07:01, 13 September 2022 (UTC)
- I took almost the reverse approach. Estimate phone height is 0.2 metres, Planck length is 1.6e-35 metres, ratio is 1.25e34, then take the 101th root. That would give about 2.176 as the reduction factor, which is also the screen aspect ratio. Then ask, "how far off might this be?" I assumed the 101th reduction is just barely smaller than the Planck length, it could be almost another reduction and still work. In other words, the aspect ratio is constrained to be between the 101th root and the 102nd root of the screen height in Planck units. With a 20 cm high screen, that puts the aspect ratio between 2.159 and 2.176 -- so the 9:20 aspect ratio (2.222) is completely ruled out. However
- This question assumes it is the same phone screen being used for every screenshot. That seems to be unlikely to me. Wouldn't the reason for taking a screenshot be to share it with others? Also, my Samsung phone saves screenshots as JPEG images, which are lossy. Does the iPhone save screenshots lossless? I would love to see the image degradation caused by so many repeated lossy saves! 162.158.222.211 07:40, 15 September 2022 (UTC)
This seems like it could actually be really cool. Can anyone do this and put the picture here as an example? Also, if possible, include an AI upscale of the one pixel. 172.69.90.83 19:07, 12 September 2022 (UTC)
There's a minor counting error: instead of pointing to the 9th rotation, the 'nine rotations' statement points to the 8th as the first phone has no rotations.172.70.90.77 19:10, 12 September 2022 (UTC)
- That error is also on the 25 rotation, in both cases he counts the first screen with, and thus is one rotation behind. Also there are only 99 screens and thus 98 rotations so he missed the last 3 rotations, and screens, as there should have been 102 screens. --Kynde (talk) 09:06, 13 September 2022 (UTC)
Anyone getting a 404? Seems like the comic has disappeared. EDIT: ...aaaand it's back. 172.70.100.54 19:34, 12 September 2022 (UTC)
Just putting https://www.codeguru.com/multimedia/rotate-a-bitmap-image/ here. 172.69.134.131 20:12, 12 September 2022 (UTC)
- Microsoft C#, and not the original HAKMEM or Smalltalk 80? Please! You might as well be using C++: https://docs.microsoft.com/en-us/windows/win32/api/wingdi/nf-wingdi-plgblt 162.158.166.173 20:21, 12 September 2022 (UTC)
- I see your trivial software squabble, and raise one peer reviewed open access article citation: https://link.springer.com/article/10.1007/s10648-010-9144-5 172.69.22.5 22:03, 12 September 2022 (UTC)
- I'll see your humorously ambiguous reference, and raise you a slightly more on-topic chapter encompassing both: https://journalspress.com/LJRHSS_Volume17/208_The-Geometric-Progression.pdf 162.158.166.125 22:10, 12 September 2022 (UTC)
- I see your trivial software squabble, and raise one peer reviewed open access article citation: https://link.springer.com/article/10.1007/s10648-010-9144-5 172.69.22.5 22:03, 12 September 2022 (UTC)
Tiktok 108.162.246.68 20:40, 12 September 2022 (UTC)
Where would the rotated photograph bar be on 1909: Digital Resource Lifespan? 172.70.211.50 22:14, 12 September 2022 (UTC)
Doing this with an jpeg does the same. When rotating an image and saving it the lossy compression will lose more pixels. This makes it more blurry each step. 162.158.203.38 22:41, 12 September 2022 (UTC)
- Who said it had to be something like JPEG? Since the information added at each step is known and finite, you could easily devise an iterated rotated image format that perfectly preserves the detail at every level down to the Planck length, and provide the possibility of zooming in on the screen all the way down. Of course you couldn't *display* all the detail at every level at the same time, but you could certainly store it in a hypothetical IRI (tm) format. 172.70.162.147 16:00, 13 September 2022 (UTC)
I'm skeptical of "details at a sub-pixel level but that would have been significant if recorded at a greater resolution cannot emerge" -- this is subjective at a couple levels, and not as entirely impossible as opposed to just vaguely unlikely as the italics imply. 172.69.22.119 00:43, 13 September 2022 (UTC)
- Well, after finding the context... Using pixel-multiplying techniques on low-res pixels (either direct, a poor imaging source, or upon previously downsampled high-res one) will either never recreate features 'lost' in the lower resolution or will always do (or at least always in a given non-zero proportion of pixel-patternations indistinguishable from the more justified one) even in situations where there was no justification for such an algorithmically-invoked artefact.
- But I suppose the most perfect fractal-compression, if it matches 'reality' well enough, could be rediscovered by the statistical pixel analysis which then extrapolates (or interpolates) all kinds of image details that were never even present even in the rawest of raw digital images but were always there to be discovered in the real-world had only the correct zoom level and framing been used. And, if you've got something that can do that, I'll up the stakes with the Photo Enhancer/Inferrer thing that Rick Deckard used... It can even interpolate around corners! 172.71.178.65 02:33, 13 September 2022 (UTC)
The title text reminds me of the CSI TV show where a reflection of a faint image would be zoomed in on and the tiny text on the original could be read clearly.172.70.100.136 11:13, 13 September 2022 (UTC)
- After casually getting links to potentially follow up on 172.71.178.65, above, one of the interesting ones is: https://www.google.com/amp/s/scifiinterfaces.com/2020/04/29/deckards-photo-inspector/amp/ 172.70.162.77 13:17, 13 September 2022 (UTC)
I thought Randall was poking fun at all the dumb movies and TV programs that have the magic ability to “enhance” images and recover sub-pixel detail. It’s such an egregious plot point that you can recognize computer scientists by their groans in movie theaters. There’s even a TV Trope about it: https://tvtropes.org/pmwiki/pmwiki.php/Main/EnhanceButton — Also, the infinitely regressing image is called a Droste Image. --Dúthomhas (talk) 08:08, 14 September 2022 (UTC)
This comic reminds me a lot of 1683: Digital Data, which is also about degradation of images through re-posting screenshots. 162.158.222.211 09:27, 14 September 2022 (UTC)
- Absolutely no question, I spent half an hour looking for that one. Added; thanks! 172.70.211.162 21:03, 14 September 2022 (UTC)
" This is funny because the default resolution of contemporary camera phones can be too large to meet size requirements for e.g. mobile phone Multimedia Messaging Service, web file uploads, or email attachments, so one or two steps of this awkward procedure are sometimes necessary." - if true (presumedly screen-res and thus screencap-res is lower than the camera output, so after the image viewer is used to effectively downscale (maybe even pinch-zoom in and reframe the image) without using an actual image-editor/cropper app) then I don't see why two steps are necessary. The second scrcap step has the same number of pixels as the first... But, hey, it sounds like a kludge anyway. And I just thought I'd comment, don't mind me. (Can't see how "this is funny because", though. This is lacking all the humour of the almost-literal reductio ad absurdum already demonstrated and discussed. I don't think many times "This is funny because..." has been a useful thing to add to an Explanation, even if that's the intention of the site.) 172.71.178.65 10:57, 15 September 2022 (UTC)
- What's more useful on this site than explaining the jokes? If you want to teach people how to fish, you should be on WikiHow. 172.70.210.209 22:11, 16 September 2022 (UTC)
- "This is funny because..." is redundant if true, I would say. The explanation can reveal the humour explicitly or by cluing the reader into it, but those four extra words add nothing. And subtract much when wrong. Interesting interpretations (like the above? Do people actually downscale by screenshotting?) may add to understanding, but not any humour. And then the statement is wrong, as it stands. That's without the "...or two steps", which I also think is just plain wrong, just never got around to editing out. 172.70.90.61 00:30, 17 September 2022 (UTC)
A similar case in real life: https://9gag.com/gag/aL2e3YM 198.41.231.180 (talk) 13:41, 21 September 2022 (please sign your comments with ~~~~)
"(Why was '.' being used instead of '*' for multiplication?)" – possibly because it's one of the various valid notations in use, although I might have used x•a, or even just gone for xa, myself. Just a matter of style choice, really, though there are indeed many different styles that some situations might (differently) stronly suggest. But it's perfectly understandable in context. 172.71.178.64 14:31, 19 June 2023 (UTC)