Difference between revisions of "2509: Useful Geometry Formulas"
m (rv) |
|||
| Line 1: | Line 1: | ||
| − | + | {{comic | |
| + | | number = 2509 | ||
| + | | date = August 30, 2021 | ||
| + | | title = Useful Geometry Formulas | ||
| + | | image = useful_geometry_formulas.png | ||
| + | | titletext = Geometry textbooks always try to trick you by adding decorative stripes and dotted lines. | ||
| + | }} | ||
| + | |||
| + | ==Explanation== | ||
| + | {{incomplete|Created by a STRIPED AND DOTTED TEXTBOOK ILLUSTRATOR. Explain the formulas for each of the areas, and also the correct formula for the 3D object they seem to represent. Consider whether to add a table with the formula given and the correct formula for the 3D shape. Do NOT delete this tag too soon.}} | ||
| + | This comic showcases area formulas for the areas of four two-dimensional geometric shapes which each have extra dotted and/or solid lines making them look like illustrations for 3-dimensional objects. The first, a simple equation for the area of a circle, the second an equation for the area of a triangle with a semi-elliptic base, the third an equation for the area of a rectangle with an elliptical base and top, and the fourth an equation for the area of a hexagon consisting of two opposing right-angled corners and two parallel diagonal lines connecting their sides. In each case, only the area formed by the outline of each shape is calculated. | ||
| + | |||
| + | Similar illustrations are commonly found in geometry textbooks, which are used to depict three-dimensional figures on a two-dimensional page. They commonly make use of slanted lines to indicate edges receding into the distance and dashed lines to indicate an edge occluded by nearer parts of the solid. The joke is that the formulae given here are for the area of each two-dimensional shape within its outer solid lines, not for the surface area or volume of the illustrated 3D object (as would be shown in the geometry textbook). The title text continues the joke by claiming that the dotted lines are simply decorative. | ||
| + | |||
| + | The illustrations depict the following plane or solid figures, depending on the interpretation. | ||
| + | |||
| + | ; Top Left - Circle with an inscribed ellipse, or Sphere | ||
| + | This illustration is commonly used to depict a three-dimensional sphere, with the ellipse representing a "horizontal" or axial cross-section through the center; the solid lower half of the ellipse represents the "front" of the circumference of this cross-section, while the dotted upper half represents the "back" of the same section, which would be occluded from view if this were a solid shape. | ||
| + | |||
| + | The radius of the circle, from the center to the right edge where it meets the ellipse, is labeled 'r'. In a textbook diagram of a sphere, the radius might be instead labeled with a diagonal line from the center to a different point on the ellipse, implying the generality that all points on that cross-section, and indeed on the whole spherical surface, are at the same radius from the center. However, this line would be shorter on the page than the actual radius, making it useless for the formula of the area of the 2D outer shape. | ||
| + | |||
| + | The area of the 2D shape on the page is the area of the circle, which is A = πr<sup>2</sup>. This is captioned below the figure. | ||
| + | |||
| + | Coincidentally the area of the horizontal cross-section of the 3D sphere, as depicted by the ellipse, is also πr<sup>2</sup>, and a reader familiar with such diagrams might initially assume that this is what was meant. However, this does not extend to the other figures. | ||
| + | |||
| + | The 3D sphere commonly depicted by this drawing would have a volume of <sup>4</sup>/<sub>3</sub> πr<sup>3</sup> and a surface area of 4πr<sup>2</sup>. | ||
| + | |||
| + | ; Top Right - Ellipse with symmetrical diagonal lines, or Cone | ||
| + | This illustration is commonly used to depict a three-dimensional right circular cone, with the lower half of the ellipse representing the "front edge" of the bottom surface, and the upper half representing the occluded "back edge". However such drawings would usually not use both 'a' and 'b' to describe the radius of the base of the cone, which is drawn as an ellipse due to foreshortening. Alternatively, the drawing could depict a right elliptical cone. | ||
| + | |||
| + | Randall approximates the area of the 2D shape on the page as the sum of the area of the triangle formed by the major axis of the ellipse and the two lines, and half of the area of the ellipse (<sup>π</sup>/<sub>2</sub> ab) since most of the upper half of the ellipse overlaps the triangle. The equation for this area is A = 1/2 πab + bh. This is captioned below the figure. | ||
| + | |||
| + | The actual area of a picture of a cone is not Randall's approximation, because the sides connect at the points on the ellipse where they can spread widest and form tangents to the ellipse, and such points are a little higher than those which define the major axis. This is most obvious in cases when h is only a little larger than a. The area can be computed to be exactly A = b (a arccos(-a/h)) + √(h<sup>2</sup>-a<sup>2</sup>)). | ||
| + | |||
| + | The 3D right circular cone commonly depicted by this drawing would have a volume of πr<sup>2</sup>h/3 where r=a=b. The area of the "lower" surface would be πr<sup>2</sup>, while the surface area of the upper conical surface would be πr√(h<sup>2</sup> + r<sup>2</sup>). Neither of these areas can correspond with the caption in the comic, nor does the total surface area (the sum of these two). | ||
| + | |||
| + | If we do not assume that a = b, this drawing could also depict a right elliptic cone. The volume of the elliptic cone would be <sup>π</sup>/<sub>3</sub> abh. The area of the lower surface would be πab and the area of the curved upper surface would be <br>2a√(b<sup>2</sup> + h<sup>2</sup>) <sub>0</sub>∫<sup>1</sup> √(<sup>a²h²(t²-1) - b²(a²+h²t²)</sup>/<sub>a²(t²-1)(b²+h²)</sub>) dt. | ||
| + | |||
| + | ; Bottom Left - Two ellipses joined vertically, or Cylinder | ||
| + | This illustration is commonly used to depict a 3D cylinder or right circular prism. In this case, the upper ellipse represents the "visible" part of the top circular surface, with its "depth" shorter than its "width" due to foreshortening, and the lower part of the lower ellipse represents the "front" edge of the lower surface; the dotted half of the lower ellipse represents the occluded "back" edge of the lower surface. | ||
| + | |||
| + | To add to the confusion, the upper ellipse has its major axis labeled 'd' which usually denotes the diameter of a circular surface, while the lower ellipse has its semimajor axis labeled 'r' which similarly denotes a radius, even though the ellipses drawn have neither diameter nor radius. The 'h' denoting height is also used for both rectangles and solid objects. While 'd' in this case is required for the area calculation of the 2D shape, in textbooks only 'r' may be marked and the arrow may be offset at a diagonal rather than in line with any figurative axis, to imply its applicability to any angle of radius. | ||
| + | |||
| + | The non-overlapping parts of the 2D shape are composed of the rectangle formed by the major axes of the two ellipses and the vertical lines, plus half of the top ellipse and half of the bottom ellipse. The area of the rectangle is dh, and the area of an ellipse with semimajor axis d/2 and semiminor axis r is πrd/2. The total area is A = d(πr/2 + h), which is captioned below the figure. | ||
| + | |||
| + | A 3D right circular prism (cylinder) would have a volume of πr<sup>2</sup>h and a surface area of 2πr<sup>2</sup> + πdh, or 2πr(r + h) since in this case d = 2r. The area of each flat surface would be πr<sup>2</sup>. If we do not assume d = 2r, then the lateral surface area of the right elliptic cylinder is 4h <sub>0</sub>∫<sup>1</sup> √(<sup>1 - t²(1-4r²/d²)</sup>/<sub>1 - t²</sub>) dt. The volume is <sup>π</sup>/<sub>2</sub> rdh. | ||
| + | |||
| + | ; Bottom Right - Parallel Hexagon, or Prism | ||
| + | This illustration is commonly used to depict a rectangular prism, with 'b' denoting the 'breadth', 'd' the 'depth' and 'h' the 'height'. However, the labeled angle θ, which is necessary for the area calculation of the 2D shape, would not normally be used in a diagram of a rectangular prism, as all angles are assumed to be right angles. A rhomboidal prism could be accurately described by this diagram with the assumption that the 'base' parallelogram is perpendicular to the 'front' and that the only non-right angle is θ. In that case 'd' would not accurately describe the depth of the solid, which would be d sin θ. | ||
| + | |||
| + | The area of the 2D shape is comprised of the rectangle at the lower left, the parallelogram above it, and the parallelogram on the right. The area of the rectangle representing the front face of the prism is bh. The area of the upper parallelogram is db sin θ. The area of the right parallelogram is dh cos θ. The equation for this area is A = bh + d(b sinθ + h cosθ) as is given below the figure. | ||
| + | |||
| + | The surface area of the prism would be 2bh + 2db sin θ + 2dh. The volume is bdh sin θ. Assuming a 3D shape, θ can be artificially altered by the projection; the assumption could be made that θ is 90 degrees, and sin θ is 1 (and therefore can be eliminated from the formulas), but since θ is marked, such an assumption might not be valid. | ||
| + | |||
| + | In the history of the development of computer-generated 3D graphics, calculations of the apparent visual area taken up by the projection of a volume may have been useful in occlusion-like optimizations, where each drawn pixel may be passed through many fragment shaders. | ||
| + | |||
| + | ==Transcript== | ||
| + | {{incomplete transcript|Do NOT delete this tag too soon.}} | ||
| + | :[Four figures in two rows of two, each being a common two-dimensional representation of a three-dimensional object, with solid lines in front and dotted lines behind. Each figure has some labeled dimensions represented with arrows and a formula underneath indicating its area. Above the four figures is a header:] | ||
| + | :Useful geometry formulas | ||
| + | |||
| + | :[Top left; A circle with an inscribed concentric ellipse sharing its horizontal diameter. The edge of the ellipse above the major axis is drawn with a dotted line, while the lower edge is drawn with a solid line, similar to textbook depictions of a 3D sphere. The shared radius/semi-major axis to the right of the center is drawn as an arrow and labeled 'r'. ] | ||
| + | :A = πr² | ||
| + | |||
| + | :[Top right; An ellipse with horizontal major axis, plus two straight lines: one from each end of the major axis, up to a point vertical to the center of the ellipse, so that the major axis of the ellipse (not drawn) and the two lines would form an isosceles triangle with a vertical axis of symmetry. The upper edge of the ellipse above the major axis is drawn with a dotted line, while the lower edge is drawn with a solid line, similar to textbook depictions of a right elliptical cone, or more commonly a right circular cone. The semi-minor axis of the ellipse is drawn with an arrow down from the center and labeled 'a' and the semi-major axis is similarly drawn to the right of the center and labeled 'b'. To the right of the shape, the height of the isosceles triangle is drawn using arrows, and labeled 'h'.] | ||
| + | :A = 1/2 πab + bh | ||
| + | |||
| + | :[Bottom left; Two ellipses of the same dimensions, with major axes horizontal, drawn vertically one above the other, with vertical lines connecting each end of the major axis of the top ellipse to the corresponding points on the bottom ellipse. The upper edge of the bottom ellipse above the major axis is drawn with a dotted line, while the lower edge is drawn with a solid line, similar to textbook depictions of a right elliptical prism or, more commonly, a right cylinder (circular prism). Inside the shape, the major axis of the upper ellipse is drawn as a double-ended arrow and labeled 'd'. The semi-minor axis of the lower ellipse is drawn as an arrow down from the center and labeled 'r'. To the right of the shape, the length of the vertical lines is replicated using arrows and labeled 'h'. ] | ||
| + | :A = d(πr/2 + h) | ||
| + | |||
| + | :[Bottom right; Two rectangles of the same vertical and horizontal dimensions, drawn with one offset diagonally to the upper right of the other, with diagonal lines connecting the corresponding vertices, forming a hexagon with opposite sides parallel. The upper right rectangle has its left and bottom sides drawn with dotted lines, and a similar dotted line is used connecting the bottom left corner of the two rectangles, similar to textbook depictions of rhomboid-based right prisms, or more commonly rectangular prisms. Outside the shape, the bottom edge of the lower rectangle is redrawn below the shape with arrows and labeled 'b'. The length of the left edge is similarly redrawn to the left and labeled 'h'. The length of the diagonal line connecting the upper left corners of the two rectangles is similarly redrawn on the top left using arrows and labeled 'd'. The acute angle between the bottom edge of the lower rectangle, and the dotted diagonal connecting the two lower left corners, is labeled 'θ'] | ||
| + | :A = bh + d(b sinθ + h cosθ) | ||
| + | |||
| + | {{comic discussion}} | ||
| + | |||
| + | [[Category:Math]] | ||
Revision as of 22:12, 4 May 2022
| Useful Geometry Formulas |
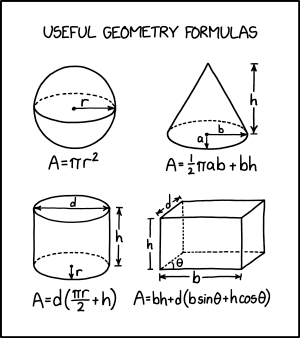 Title text: Geometry textbooks always try to trick you by adding decorative stripes and dotted lines. |
Explanation
| |
This explanation may be incomplete or incorrect: Created by a STRIPED AND DOTTED TEXTBOOK ILLUSTRATOR. Explain the formulas for each of the areas, and also the correct formula for the 3D object they seem to represent. Consider whether to add a table with the formula given and the correct formula for the 3D shape. Do NOT delete this tag too soon. If you can address this issue, please edit the page! Thanks. |
This comic showcases area formulas for the areas of four two-dimensional geometric shapes which each have extra dotted and/or solid lines making them look like illustrations for 3-dimensional objects. The first, a simple equation for the area of a circle, the second an equation for the area of a triangle with a semi-elliptic base, the third an equation for the area of a rectangle with an elliptical base and top, and the fourth an equation for the area of a hexagon consisting of two opposing right-angled corners and two parallel diagonal lines connecting their sides. In each case, only the area formed by the outline of each shape is calculated.
Similar illustrations are commonly found in geometry textbooks, which are used to depict three-dimensional figures on a two-dimensional page. They commonly make use of slanted lines to indicate edges receding into the distance and dashed lines to indicate an edge occluded by nearer parts of the solid. The joke is that the formulae given here are for the area of each two-dimensional shape within its outer solid lines, not for the surface area or volume of the illustrated 3D object (as would be shown in the geometry textbook). The title text continues the joke by claiming that the dotted lines are simply decorative.
The illustrations depict the following plane or solid figures, depending on the interpretation.
- Top Left - Circle with an inscribed ellipse, or Sphere
This illustration is commonly used to depict a three-dimensional sphere, with the ellipse representing a "horizontal" or axial cross-section through the center; the solid lower half of the ellipse represents the "front" of the circumference of this cross-section, while the dotted upper half represents the "back" of the same section, which would be occluded from view if this were a solid shape.
The radius of the circle, from the center to the right edge where it meets the ellipse, is labeled 'r'. In a textbook diagram of a sphere, the radius might be instead labeled with a diagonal line from the center to a different point on the ellipse, implying the generality that all points on that cross-section, and indeed on the whole spherical surface, are at the same radius from the center. However, this line would be shorter on the page than the actual radius, making it useless for the formula of the area of the 2D outer shape.
The area of the 2D shape on the page is the area of the circle, which is A = πr2. This is captioned below the figure.
Coincidentally the area of the horizontal cross-section of the 3D sphere, as depicted by the ellipse, is also πr2, and a reader familiar with such diagrams might initially assume that this is what was meant. However, this does not extend to the other figures.
The 3D sphere commonly depicted by this drawing would have a volume of 4/3 πr3 and a surface area of 4πr2.
- Top Right - Ellipse with symmetrical diagonal lines, or Cone
This illustration is commonly used to depict a three-dimensional right circular cone, with the lower half of the ellipse representing the "front edge" of the bottom surface, and the upper half representing the occluded "back edge". However such drawings would usually not use both 'a' and 'b' to describe the radius of the base of the cone, which is drawn as an ellipse due to foreshortening. Alternatively, the drawing could depict a right elliptical cone.
Randall approximates the area of the 2D shape on the page as the sum of the area of the triangle formed by the major axis of the ellipse and the two lines, and half of the area of the ellipse (π/2 ab) since most of the upper half of the ellipse overlaps the triangle. The equation for this area is A = 1/2 πab + bh. This is captioned below the figure.
The actual area of a picture of a cone is not Randall's approximation, because the sides connect at the points on the ellipse where they can spread widest and form tangents to the ellipse, and such points are a little higher than those which define the major axis. This is most obvious in cases when h is only a little larger than a. The area can be computed to be exactly A = b (a arccos(-a/h)) + √(h2-a2)).
The 3D right circular cone commonly depicted by this drawing would have a volume of πr2h/3 where r=a=b. The area of the "lower" surface would be πr2, while the surface area of the upper conical surface would be πr√(h2 + r2). Neither of these areas can correspond with the caption in the comic, nor does the total surface area (the sum of these two).
If we do not assume that a = b, this drawing could also depict a right elliptic cone. The volume of the elliptic cone would be π/3 abh. The area of the lower surface would be πab and the area of the curved upper surface would be
2a√(b2 + h2) 0∫1 √(a²h²(t²-1) - b²(a²+h²t²)/a²(t²-1)(b²+h²)) dt.
- Bottom Left - Two ellipses joined vertically, or Cylinder
This illustration is commonly used to depict a 3D cylinder or right circular prism. In this case, the upper ellipse represents the "visible" part of the top circular surface, with its "depth" shorter than its "width" due to foreshortening, and the lower part of the lower ellipse represents the "front" edge of the lower surface; the dotted half of the lower ellipse represents the occluded "back" edge of the lower surface.
To add to the confusion, the upper ellipse has its major axis labeled 'd' which usually denotes the diameter of a circular surface, while the lower ellipse has its semimajor axis labeled 'r' which similarly denotes a radius, even though the ellipses drawn have neither diameter nor radius. The 'h' denoting height is also used for both rectangles and solid objects. While 'd' in this case is required for the area calculation of the 2D shape, in textbooks only 'r' may be marked and the arrow may be offset at a diagonal rather than in line with any figurative axis, to imply its applicability to any angle of radius.
The non-overlapping parts of the 2D shape are composed of the rectangle formed by the major axes of the two ellipses and the vertical lines, plus half of the top ellipse and half of the bottom ellipse. The area of the rectangle is dh, and the area of an ellipse with semimajor axis d/2 and semiminor axis r is πrd/2. The total area is A = d(πr/2 + h), which is captioned below the figure.
A 3D right circular prism (cylinder) would have a volume of πr2h and a surface area of 2πr2 + πdh, or 2πr(r + h) since in this case d = 2r. The area of each flat surface would be πr2. If we do not assume d = 2r, then the lateral surface area of the right elliptic cylinder is 4h 0∫1 √(1 - t²(1-4r²/d²)/1 - t²) dt. The volume is π/2 rdh.
- Bottom Right - Parallel Hexagon, or Prism
This illustration is commonly used to depict a rectangular prism, with 'b' denoting the 'breadth', 'd' the 'depth' and 'h' the 'height'. However, the labeled angle θ, which is necessary for the area calculation of the 2D shape, would not normally be used in a diagram of a rectangular prism, as all angles are assumed to be right angles. A rhomboidal prism could be accurately described by this diagram with the assumption that the 'base' parallelogram is perpendicular to the 'front' and that the only non-right angle is θ. In that case 'd' would not accurately describe the depth of the solid, which would be d sin θ.
The area of the 2D shape is comprised of the rectangle at the lower left, the parallelogram above it, and the parallelogram on the right. The area of the rectangle representing the front face of the prism is bh. The area of the upper parallelogram is db sin θ. The area of the right parallelogram is dh cos θ. The equation for this area is A = bh + d(b sinθ + h cosθ) as is given below the figure.
The surface area of the prism would be 2bh + 2db sin θ + 2dh. The volume is bdh sin θ. Assuming a 3D shape, θ can be artificially altered by the projection; the assumption could be made that θ is 90 degrees, and sin θ is 1 (and therefore can be eliminated from the formulas), but since θ is marked, such an assumption might not be valid.
In the history of the development of computer-generated 3D graphics, calculations of the apparent visual area taken up by the projection of a volume may have been useful in occlusion-like optimizations, where each drawn pixel may be passed through many fragment shaders.
Transcript
| |
This transcript is incomplete. Please help editing it! Thanks. |
- [Four figures in two rows of two, each being a common two-dimensional representation of a three-dimensional object, with solid lines in front and dotted lines behind. Each figure has some labeled dimensions represented with arrows and a formula underneath indicating its area. Above the four figures is a header:]
- Useful geometry formulas
- [Top left; A circle with an inscribed concentric ellipse sharing its horizontal diameter. The edge of the ellipse above the major axis is drawn with a dotted line, while the lower edge is drawn with a solid line, similar to textbook depictions of a 3D sphere. The shared radius/semi-major axis to the right of the center is drawn as an arrow and labeled 'r'. ]
- A = πr²
- [Top right; An ellipse with horizontal major axis, plus two straight lines: one from each end of the major axis, up to a point vertical to the center of the ellipse, so that the major axis of the ellipse (not drawn) and the two lines would form an isosceles triangle with a vertical axis of symmetry. The upper edge of the ellipse above the major axis is drawn with a dotted line, while the lower edge is drawn with a solid line, similar to textbook depictions of a right elliptical cone, or more commonly a right circular cone. The semi-minor axis of the ellipse is drawn with an arrow down from the center and labeled 'a' and the semi-major axis is similarly drawn to the right of the center and labeled 'b'. To the right of the shape, the height of the isosceles triangle is drawn using arrows, and labeled 'h'.]
- A = 1/2 πab + bh
- [Bottom left; Two ellipses of the same dimensions, with major axes horizontal, drawn vertically one above the other, with vertical lines connecting each end of the major axis of the top ellipse to the corresponding points on the bottom ellipse. The upper edge of the bottom ellipse above the major axis is drawn with a dotted line, while the lower edge is drawn with a solid line, similar to textbook depictions of a right elliptical prism or, more commonly, a right cylinder (circular prism). Inside the shape, the major axis of the upper ellipse is drawn as a double-ended arrow and labeled 'd'. The semi-minor axis of the lower ellipse is drawn as an arrow down from the center and labeled 'r'. To the right of the shape, the length of the vertical lines is replicated using arrows and labeled 'h'. ]
- A = d(πr/2 + h)
- [Bottom right; Two rectangles of the same vertical and horizontal dimensions, drawn with one offset diagonally to the upper right of the other, with diagonal lines connecting the corresponding vertices, forming a hexagon with opposite sides parallel. The upper right rectangle has its left and bottom sides drawn with dotted lines, and a similar dotted line is used connecting the bottom left corner of the two rectangles, similar to textbook depictions of rhomboid-based right prisms, or more commonly rectangular prisms. Outside the shape, the bottom edge of the lower rectangle is redrawn below the shape with arrows and labeled 'b'. The length of the left edge is similarly redrawn to the left and labeled 'h'. The length of the diagonal line connecting the upper left corners of the two rectangles is similarly redrawn on the top left using arrows and labeled 'd'. The acute angle between the bottom edge of the lower rectangle, and the dotted diagonal connecting the two lower left corners, is labeled 'θ']
- A = bh + d(b sinθ + h cosθ)
Discussion
Area formulas are for 2D object as seen instead of surface of a projected 3D object. Sebastian --162.158.89.200 02:36, 31 August 2021 (UTC)
The "decorative stripes and dotted lines" are the parts of the diagrams that are intended to indicate the third dimension. The conceit of the comic is that these are superfluous. Barmar (talk) 02:56, 31 August 2021 (UTC)
- Can you "see" this as 2D?
One aspect of this comic that has not been mentioned is how strong the dashed line convention is if you are very familiar with these sorts of representations. I found it almost impossible to force my brain to see this as a 2D diagram with solid and (superflous) dashed lines. That third dimension just keeps popping out, although I could occasionally reverse the convention and see the dashed lines as in front rather than in back. Arl guy (talk) 14:27, 2 September 2021 (UTC)
Can someone explain how the last one works? GcGYSF(asterisk)P(vertical line)e (talk) 04:28, 31 August 2021 (UTC)
- bh is the area of the front face. The top face is a parallelogram with sides d and b, with an angle of θ between them, so its area is d b sin(θ). The right face is a parallelogram with sides d and h, with an angle of 90º - θ between them, so its area is h d sin(90º - θ) = h d cos(θ). So the area of the whole picture is bh + d b sin(θ) + d h cos(θ).
- --172.68.24.165 04:46, 31 August 2021 (UTC)
- In case you don't know the area of a parallelogram by heart, you can read d b sin(θ) as b * d sin(θ), where d sin(θ) is the height of the parallelogram; if you cut the right corner of the parallelogram off and add it on the left, you get a rectangle where the bottom side is b and the height is that d sin(θ), so it works out. The other parallelogram's area is h * d cos(θ), with the same reasoning. 162.158.90.241 05:00, 31 August 2021 (UTC)
Funnily enough, both this comic and 2506 are about projection. CRLF (talk) 05:11, 31 August 2021 (UTC)
- I had considered working that into the explanation, but that needs to account for the fact that the indicated measurements (e.g. the angle θ) have to be read in 2D, not in 3D and projected. But it would be correct to say that the 2D shapes are projections of simple 3D objects. 162.158.90.149 05:23, 31 August 2021 (UTC)
- Between this, 2506, and all the ones about Mercator and other map projections ... "projection" is a very large word in Randall's brain's word cloud. 172.69.63.8 15:29, 31 August 2021 (UTC)
- Feels to me like every comic since 2500 could be tagged "projection" in one sense of the word or another. --172.69.69.225 21:55, 31 August 2021 (UTC)
- Does the bottom-left formula have a mistake?</s>
It seems like the bottom-left formula should be A=d(πr+h) rather than A=d(πr/2+h), because there are two half-ellipses that add up to a complete ellipse. Am I missing something? (This doesn't seem like an extra joke, does it?) 162.158.106.179 05:28, 31 August 2021 (UTC)
- No, it's correct. d is all of the major axis, not just half, so we have to divide that by 2. 162.158.92.83 05:51, 31 August 2021 (UTC)
- Oh, right; good call! 162.158.106.179 06:49, 31 August 2021 (UTC)
- Does the top-right formula have a mistake?
I think it should be in brackets, the top triangle area needs the 1/2 also, so it should be: A=1/2(πab + bh)
- No, it's correct. The bottom is a half ellipse, with area 1/2 π a b, and the top is a triangle with base 2 b and height h, so its area is 1/2 2b h = bh. The total area is 1/2 π a b + b h.
--172.68.25.144 06:49, 31 August 2021 (UTC)
- 3D formulae for reference
4πr^2
πb(a+√(b^2+h^2)) if a=b
πr(2r+h)
2(bd+bh+dh)
162.158.107.80 09:54, 31 August 2021 (UTC)
- It would be clarifying to add these to the comic, but of course they are flagrantly wrong. Baffo32 (talk) 09:57, 31 August 2021 (UTC)
- Surely ripe for a table, in place of much of the longhand paragraph spiel (which could be kept, but simpler for just the narrative but otherwise non-technical details)... "Shape (2D)", "Area", "Pretended Shape (3D)", "Surface Area", "Volume", ¿"Notes"? (Not sure about specific Notes, some things could/should be said below the formulae/descriptions in the relevent cell to which that matters, in special cases where necessary, which might be better than a Notes either empty or jammed up with all the combined row-specific corollaries, etc, that I can imagine.) Anyway, an idea. 141.101.76.11 11:56, 31 August 2021 (UTC)
- I think the formulas are correct. Those given should be from the text book, not for those with ellipse bases. Someone has put a lot of work into giving these complicated formulas for the cone and cylinder. But I think that is overkill. I have added to the explanation the simple versions before, and would suggest deleting the complicated, which was never the intention of either text book or Randall! ;-)--Kynde (talk) 12:36, 31 August 2021 (UTC)
- What complicate formulae?? --GcGYSF(asterisk)P(vertical line)e (talk) 20:28, 4 September 2021 (UTC)
- I think the formulas are correct. Those given should be from the text book, not for those with ellipse bases. Someone has put a lot of work into giving these complicated formulas for the cone and cylinder. But I think that is overkill. I have added to the explanation the simple versions before, and would suggest deleting the complicated, which was never the intention of either text book or Randall! ;-)--Kynde (talk) 12:36, 31 August 2021 (UTC)
- Surely ripe for a table, in place of much of the longhand paragraph spiel (which could be kept, but simpler for just the narrative but otherwise non-technical details)... "Shape (2D)", "Area", "Pretended Shape (3D)", "Surface Area", "Volume", ¿"Notes"? (Not sure about specific Notes, some things could/should be said below the formulae/descriptions in the relevent cell to which that matters, in special cases where necessary, which might be better than a Notes either empty or jammed up with all the combined row-specific corollaries, etc, that I can imagine.) Anyway, an idea. 141.101.76.11 11:56, 31 August 2021 (UTC)
- Surface area. Not volume. My bad. I usually consider volume associated with pics like like that. Don't use surface area much. Baffo32 (talk) 22:22, 1 September 2021 (UTC)
add an extra edited image that is the comic without dotted lines to make it easier to see the 2d shapes? 172.69.71.177 12:46, 31 August 2021 (UTC)Bampf
- And an animated GIF of the 3D solid objects rotating to show their real shapes. At different speeds. If you have the time. :-) Robert Carnegie [email protected] 141.101.76.11 16:31, 31 August 2021 (UTC)
- Image here: https://i.imgur.com/dq7VmnK.png Editing done myself, feel free to upload it to this wiki if you have an account on this wiki. :) --162.158.88.29 17:22, 1 September 2021 (UTC)
Please do check my (additional) changes to the bottom-right item (hexagon-cum-prism) in both main and transcript texts. As hinted in my edit notes, cos-theta is important because the skewed tetrahedron (rhomboid, whether in plan or the true area of the 'fake' perspective) is not d*b in area. The fact that without the theta it would look like a standard oblique orthographic projection with entirely right-angled corners is perhaps part of the (intended?) confusion, although we can probably assume that all unmarked (and, of course, uncongruent/uncomplimentary) angles are 90° so that it isn't a full on parallelepiped with an additional phi-angle on an adjacent face and a complicated third dependent-angle somewhere upon the remaining face-plane. As such, I put in the cosine element to both the 3d surface formula (it only affects the bd-shape, the both of them) and the 3d volume (from this shape, extrudes without further adjustment straight up the h-axis), but I always have to second guess if I've done this simple bit of trig right, it seems, even though I should know better and just trust to SOHCAHTOA... ;) 162.158.158.146 13:24, 31 August 2021 (UTC)
- (Case in point: I thought I'd added cosines, and I'd put sines anyway, when fussing about copying the clipboarded theta-character into the right place! Re-read, seen, corrected(?) this myself. Unless I thought I was was wrong; but I was wrong, I was right!) 162.158.155.145 13:33, 31 August 2021 (UTC)
I believe both of those prism formulas should use sine theta. If theta is ninety degrees, then sine theta will be 1 (thus reducing to the rectangular case), whereas cosine of 90 degrees is zero.Tovodeverett (talk) 15:19, 31 August 2021 (UTC)
- You're right (me again, from just above), I was rushed and had been right first time, I realised while I was off-grid and it was nagging away at the back of my head. I'm better on paper (or when I can sanity-test real code, but for some reason tapping it in like this just screws my mind up, taking away/inverting my technical ability and reason. (I blame the microwaves emitting from my tablet... pass the tinfoil hat!) 162.158.158.178 16:29, 31 August 2021 (UTC)
Unconvinced by the cone! The equation shown, is correct for an isosceles triangle with a half-ellipse on its base. But that shape has 'corners' where the sides meet that half-ellipse. In a 3D projected view of an actual cone, the sides will meet the base ellipse at a tangent, meaning that it is more than a half-ellipse. But I suppose it's close enough as an approximation...172.69.55.131 15:57, 1 September 2021 (UTC)
- I verified your claim by imagining the surface of the cone as formed by a set of lines extending from the different points on the ellipse to a single fixed point at the tip. No matter where you put that tip point, the outermost lines seem tangent to the ellipse. Seems it works for both perspective and orthographic projections. Updated the explanation. Randall's formula is incorrect, especially for very short cone projections. Baffo32 (talk) 22:46, 1 September 2021 (UTC)
- I expanded the text slightly, and worked out the correct formula: it should be (2π - 2arctan(h/a))ab + b sqrt(h^2 - a^2). Can someone verify that, format it properly for the wiki, and add it? The easy way to check it is to shrink the diagram horizontally so the ellipse is a circle of radius a. (Does the wiki not have MathJax or similar installed? Seems odd, given Randall Munroe's interests.) It's maybe also worth mentioning that looking closely at the picture at a pixel level shows that he did draw the tangents, rather than do the half-ellipse + triangle that the formula suggests. --172.69.90.75 16:48, 2 September 2021 (UTC)
- It's 3am (okay 5am) and I made it really long!
I just followed the directions in the "incomplete" which said to add in explanations of the formulae ... Please feel free to edit to take out redundancy. However I did add in the following explanations: - the fact that the formula in the third figure is actually the same as the cross-section represented by the ellipse, which is why you may not get the joke after reading the first picture; - the use of 'd', 'r' and 'h' in the third figure, which adds to the confusion as they imply "diameter", "radius" and "height" - the fact that the area calculations must take into account the overlapping shapes (there were previously references to "semi-ellipses" which are extrapolations, not what's drawn there) Haven't yet done the last figure - pretty sure 'b' 'd' and 'h' are for 'breadth', 'depth' and 'height' and while 'height' is also used for 2D rectangles, 'breadth' less so in maths textbooks (usually 'width') - whoever pointed out that there is a theta as well, pretty sure it's only there because it's necessary for the area calculation, as 'depth' only really applies as labelled to rectangular prisms - if the base were not rectangular, 'd' would not be equal to the 'depth' Will try to come back later and shorten... 162.158.166.40 18:56, 1 September 2021 (UTC)
Someone thought that "formulae" was a typo for "formulas" (which it might easily be, on a QWERTY or similar layout). Not going to revert, but note that (for a mathematical formula, if perhaps not a chemical one/etc, but there's plenty of mixed use) this is actually quite correct. If it were up to me alone (I didn't write that one, orother mentions like in the above Talk contribution), for the record, I'd probably have used "formulæ" myself. ;) 162.158.155.145 20:28, 1 September 2021 (UTC)
If you don't assume that the bottom right figure is 3D, what's the justification for projecting upward and assuming that the angle theta is also the angle of the top parallelogram? Arl guy (talk) 02:25, 2 September 2021 (UTC)
- If you assume that the two rectangles have equal width and height, then it can be mathematically proven that the angles must be equal (probably using congruent triangles). However this assumption is not stated on the figure. That said, you would make the same assumption for the 3D figure, along with a whole bunch of other assumptions of course.172.70.147.23 06:31, 2 September 2021 (UTC) Edit: The two rectangles must have equal width and height to make the rest of the shapes parallelograms in the first place. If they aren't identical you get trapezoids all round and possibly a bunch of different angles. 172.70.143.22 06:43, 2 September 2021 (UTC)
- Yes, I think you are mostly right, but you don't necessarily get trapezoids all around. You can move the top solid line down and to the right and rotate the top left and top right slanted lines to keep the top shape a parallelogram, but the right shape will now be a trapezoid. I think the key assumption is that all the solid and dashed lines that loop parallel are, in fact, parallel. Arl guy (talk) 14:20, 2 September 2021 (UTC)
- There's always many possible unindicated perspective tricks (or axonometric/othographic ones, as might be more appropriate) in which the components of lines and relationships towards/away from the viewer are non-zero (or not non-zero in the way expected). Various of the shapes involved could be infinitely warped with leans, curves or even highly inflected wiggles to allow some 'as expected' profile even as others that should be connected are not. (Though it would make the surface 'planes' warped and distorted, even more against the conventions of wireframe diagrams.)
- Because of dependencies, as the theta moves the other similar angles might be thetas too, or they could be kept as RAs and (?)three other chosen angles could be distorted (in or out of the page, by a calculable and entirely derivative amount) to compensate. Or, like the Triangle illusion, there's overlaid duplicate edges with not all/any vertices actually being the same, just in the same illustrated place. (Again, making a mockery of the 'simple' diagram, but we're already way past that. ;) ) 162.158.155.247 08:56, 2 September 2021 (UTC)
- Sure, but we were talking about the 2D figure and taking it at "face" value - the internal angle is defined while the ones you'd actually use for the parallelogram area calculations aren't, and neither are the dimensions of the upper rectangle. In a proper geometric figure you'd have markings showing which lengths are equal and which angles are right angles.172.70.143.22 05:38, 3 September 2021 (UTC)
Subtext??: I wonder if this comic implies that we are being transformed from 3d creatures into 2D creatures... hadaso --162.158.91.184 07:04, 5 September 2021 (UTC)
Cross-section - reword please I made a wording error in describing all points on the "cross-section" of the sphere as being equidistant from the centre, and I'm stuck on how to fix it concisely. Problem is that "cross-section" is ambiguous - I think mathematically it could mean the circle at the intersection of the hollow sphere and the plane, but to me it usually means the part of the plane where it intersects the solid sphere, which makes the statement false. I want to replace it with "circle", with the quote marks, but we're actually talking about the ellipse-cum-circle so I'm not sure if that's good enough. 172.70.142.239 11:00, 7 September 2021 (UTC)
Can somebody draw what these 2d shapes are supposed to look like?
