2327: Oily House Index
| Oily House Index |
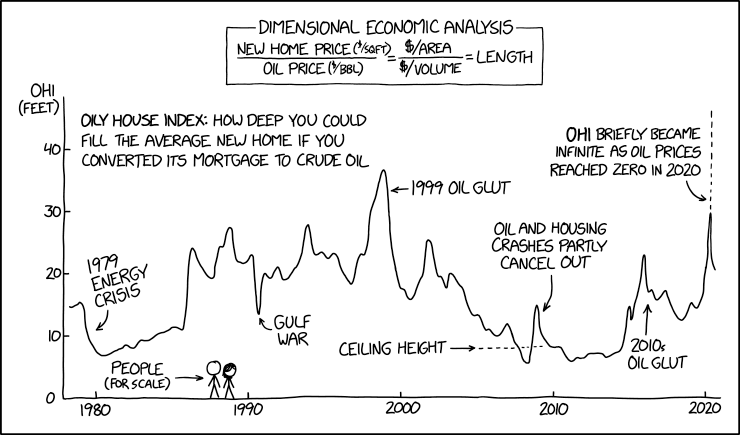 Title text: We're underwater on our mortgage thanks to the low price of water. |
Explanation
In economics, an index is a statistical measure of change in a representative group of individual data points. Common indices include NASDAQ (a measure of a range of stock prices) and a consumer price index (a measure of retail prices)
This chart demonstrates an invented index, the "Oily House Index", which measures a ratio of oil price to average house prices, over time.
The numerator is the average price of a new home (presumably in the US), in USD per square foot ($/sqft). It does not specify what kind of home, or where. One available metric is the average price per square foot of floor space in new single-family houses in the United States which was $118.91 in 2019. The caption refers to converting the mortgage of the new house (that is, how much the purchaser borrowed, which could be zero), while the definition simply refers to the new home price (the total value). It is not clear which of these two is used in the chart.
The denominator is the price of oil in USD per barrel ($/BBL). This is also not well defined, although the chart's caption suggests that it is based on crude oil. There are many different indices for different blends of oil in different locations, such as West Texas Intermediate, which is a crude oil commonly used as a global oil benchmark. (Others include Brent and Dubai Crude). The WTI price fluctuated around $55-60 throughout 2019. A barrel is a standard unit of oil volume, defined as 42 U.S. gallons (roughly 5.615 cubic feet or 0.16 cubic meters).
The comic then applies dimensional analysis to this index: dividing $/sqft by $/bbl yields a result whose dimension is a linear measurement, which can be called length. 1 barrel is 42 gallons, a gallon is 231 cubic inches, and a cubic foot is 123=1728 cubic inches, so a barrel is approximately 5.6146 cubic feet and a cubic foot is approximately 0.1781 barrel. The average price per square foot of a new single-family dwelling in the USA in 2019 was about $119/square foot, while the price of oil in mid 2019 was about $60/BBL or $10.7/cubic foot. Dividing $119/square foot by $10.7/cubic foot gives approximately 11.1 foot. This is slightly lower than the value shown on the chart of around 15.
The chart's caption then interprets that length as the depth that a new home could be filled with the crude oil that could be purchased with its price. For scale Cueball and Megan has been drawn, and the ceiling height of a typical house has been indicated, showing that only in time with deep crisis will the oil not fill the house. It's also not exactly clear where the extra oil should go after a multi-story house has been filled; on the top floor, you could just take off the roof and let the oil pile up (perhaps after building some retaining walls), but on the lower floors, there's already oil above the ceiling.
The index is high when house prices are high and oil prices are low (such as during the 1999 oil glut), and low when house prices are low and oil prices are high (such as during the 1979 energy crisis). See details about the chart below.
The title text, "We're underwater on our mortgage thanks to the low price of water", is a pun. A mortgage on a property is considered to be "underwater" when the value of the mortgage exceeds the value of the property. This is bad for both the owner (who owes more money than the property is worth) and the bank (who now have a loan which is not fully secured against a default: if the property owner defaults, the bank will lose money in selling the property)- though obviously far worse for the owner.
The title text is hinting at an alternative index based on the ratio of house price to the price of water instead of oil. At the 2019 rate of $118.91/ft² and a rough average water price of $0.0015/gallon, a house would have to be filled with water to a depth of 1060 ft for the house cost to match the water cost. If the price of water fell or the house cost per square foot rose, then the index would rise, causing the house to be even deeper in water (following the metaphor of the index as filling the house with physical water). This situation could arise even if the property value remained high, although Randall may be humorously suggesting that the increase in the index would literally flood the property with water, which would then damage it, obviously decreasing its value. (If the index continues to be computed on average house prices, then this single event would not materially impact the index as a whole.)
In What If #11 "Droppings", Randall commented that "unit cancellation is weird" after making a similar calculation about fuel efficiency -- the European convention of presenting fuel mileage as "liters per 100 kilometers" represents an area (volume/distance), which can be physically interpreted as the cross-sectional area of a tube of gasoline with the total volume of fuel burned stretched out over the length of the journey.
Chart
- 1979 energy crisis
- In the wake of the Iranian Revolution, global oil supply reduced by only 4%, but caused widespread panic and a huge increase in oil price.
- Gulf War
- The Gulf War (August 1990 - Feb 1991) was the invasion of Iraq by the US, which decreased oil supplies and caused a spike in prices.
- 1999 oil glut
- In early 1999, Iraq increased its oil production, while the Asian Financial Crisis reduced demand. Prices briefly fell to as low as $16.[1]
- Ceiling height
- Reinforcing the connection with the metaphorical house filled with oil, "ceiling height" here is shown at somewhere just below 10 feet. The standard ceiling height in US homes is 9 feet for ground floor, and 8 feet on higher floors. [2]
- Only twice has the height been below ceiling height, during the 1979 energy crisis, and in the beginning of the financial crisis of 2007-2008.
- Oil and housing crashes partly cancel out
- As a result of the financial crisis of 2007-2008, oil prices crashed from $147/BBL in July 2008 to $30 in December 2008. Meanwhile, falling house prices, which had partially triggered the financial crisis, continued to slump across the US, with the Case-Shiller home price index reporting its largest ever price drop in December 2008. Since both oil price and house prices were falling, the effect of dividing one by the other means that the index didn't change significantly, remaining around 8-15 feet.
- 2010s oil glut
- In 2014-16 there was a serious surplus of crude oil, partially caused by increasing shale oil from the US and Canada, a slowdown in demand from China, and increasing fuel efficiency and use of renewable energy. Prices dropped from $125/BBL from 2012 to below $30 in January 2016. By October 2018, prices had recovered to $85/BBL. ]
- OHI briefly became infinite as oil prices reached zero in 2020
- In April 2020, the coronavirus pandemic dramatically reduced vehicle and air transport, crashing oil demand. Oil futures actually went to zero, and even below, several times: oil producers paying consumers to take their oil, to avoid the costs of storing it. Dividing anything by zero officially has no defined result, but in many thought experiments yields infinity, hence the "infinite oily house index". The graph should actually wrap around to the negative axis at this point.
Transcript
- [A line graph is shown. Above it is a rectangular frame with formulas inside. Most of the top part of the frame is removed and instead a heading is written over the missing section of the frame. The formula is written in three parts, with the first two parts having a division line with text written above and below.]
- Dimensional economic analysis
- New home price ($/sqft) / Oil price ($/BBL) = $/area / $/volume = Length
- [The graph has a labeled Y-axis with four ticks, which have values, and also the origin has a value. The X.axis is a time-line without label. There are five labeled ticks.]
- X-axis: 1980 1990 2000 2010 2020
- Y-axis label: OHI (feet)
- Y-axis: 40 30 20 10 0
- [Above the line graph there is a caption:]
- Oily House Index: How deep you could fill the average new home if you converted its mortgage to crude oil
- [The graph begins around 15 before 1980, then dips below 10, rises slowly until about 1988 when it rises sharply. It stays high but has several peaks, and one deep valley until 1999 when there is a very high peak, which then drops fast. A few more peaks, and then a decline to the lowest point in 2008, which is followed by a small peak, and then another drop. From there it stays low until 2015 when it rises quite fast and has one very high peak. It then drops of, until 2020 when there is a really sharp peak. Above the top of the peak is a dotted line extending to the top of the graph (i.e. the top of the Y-axis, not the top of the panel). Then it drops down but not very low as it reaches the present.]
- [There are six labels with arrows pointing from them to notable peaks and valleys along the graph. They are written both above and below the line. From left to right they are:]
- 1979 energy crisis
- Gulf War
- 1999 oil glut
- Oil and housing crashes partly cancel out
- 2010s oil glut
- OHI briefly became infinite as oil prices reached zero in 2020
- [From 2005-2010 there is a dotted horizontal line that hits the valley at 2008. This is labeled with an arrow pointing to it:]
- Ceiling height
- [Below the line is a drawing of Cueball and Megan standing on the X-axis near 1990. Next to them is a label with an arrow pointing to them:]
- People (for scale)
Discussion
Dangit Randall, this was my retirement plan & now everybody's gonna want to try it! ProphetZarquon (talk) 00:53, 2 July 2020 (UTC)
Negative Equity (owing more than the house is worth) shouldn't be an immediate problem under most circumstances. If the householder isn't actually wanting to move and can still afford the asked-for repayments then it doesn't change the physical situation at all. The bank has no problems so long as the household has no problems, as they ride over (temporary) pricing crashes and emerge the other side. It's when banks get nervous that the home'owners' might default and thus put pressures on them (e.g. 'negotiating' for unsustainably greater repayments or 'immediate settlement' of the unforeseen temporary deficit) that they could tip their so-called customer over the edge. And an increase of defaulting further suppresses house-prices (general availability of sell-quick homes by owners/bank and/or the reduced neighbourhood value around abandoned properties not sold nor (officially) lived in) to draw more agreements into the self-creating danger-zone. Of course it aint as simple as all that. And permanently being underwater due to coastal flooding, probably won't sit well with the actuaries behind your continuing loan if your property isn't in Innsmouth... 162.158.159.76 09:31, 2 July 2020 (UTC)
- Maths
Can someone figure out where I went wrong here?
>The comic then applies dimensional analysis to this index: dividing $/sqft by $/bbl yields a result whose dimension is a linear measurement, which can be called length. 1 barrel is 5.6 cubic feet. The average price per square foot of a new single-family dwelling in the USA in 2019 was about 119 $/sqft, while the price of oil in mid 2019 was about $60/BBL or $337/cubic foot. Dividing gives 60/337 feet-1 or about 5.61 feet. (This doesn't match the value shown on the chart of around 15, so we have done something wrong here. :))
Thanks. Stevage (talk) 00:54, 2 July 2020 (UTC)
- Since barrels are in the denominator, you have to divide by 5.6 to get the price per cubic foot. LegionMammal978 (talk) 01:00, 2 July 2020 (UTC)
($/area)/($/volume)=($/sq.ft)/($/cu.ft)=1/ft? Shouldn't the result be in ft?
- ($/sq.ft)/($/cu.ft)=($/sq.ft)*(cu.ft/$)=($*ft*ft*ft)/($*ft*ft)=ft I initially made the 1/ft mistake too, until I remembered to invert the fraction in the denominator172.69.63.155 14:53, 8 July 2020 (UTC)
- Units
Shouldn't area divided by volume be height, not length? It would also fit better with the graph. 162.158.123.173 03:41, 2 July 2020 (UTC)
- For dimensional analysis, you don't care about the physical context of the units, just about the dimension they are associated with. Height is horizontal length, so it has the dimension of length. In the context of the comic this length can be interpreted as a height, but in another context, it could be a length in a different orientation. 162.158.88.78 04:16, 2 July 2020 (UTC)
- Category
Should we start a category of dimensional analysis comics: e.g. 687, 1707, 2312 --WhiteDragon (talk) 07:41, 2 July 2020 (UTC)
- Division Error?
You can't divide by zero; which means Randall made an error. Should we update the page to reflect this? 173.245.52.67 10:25, 2 July 2020 (UTC)
- "OHI briefly became infinite as oil prices reached zero in 2020" could be read as approaching both infinity and zero; that fixes the problem 162.158.74.249 11:18, 2 July 2020 (UTC)
- Randall did not divide by zero. If the price went continually to zero the OHI would aproach infinity. Of course at the time the price hit zero (or negative), then the OHI breaks down, which is what infinite means. So he did not make any error. (Wrote this and had an edit conflict with the first reply.) --Kynde (talk) 11:20, 2 July 2020 (UTC)
- You can divide by zero, its just that those lazy mathematicians haven't defined it yet.
- Programmers have defined it but it isn't a number: x/0 = NaN (Not a Number) 108.162.216.134 11:43, 3 July 2020 (UTC)
162.158.123.155 04:04, 3 July 2020 (UTC)
- Actually, most programmers, including IEEE, define x/0 as Infinity if x > 0, -Infinity if x < 0, and NaN if x = 0 (for floating-point numbers; for integers, it's still undefined). 162.158.62.32
- We defined it; y'all just don't like what we came up with. https://en.wikipedia.org/wiki/Wheel_theory TobyBartels (talk) 06:45, 3 July 2020 (UTC)
- You can divide by zero, but it doesn't do the house any good: House divided by zero These Are Not The Comments You Are Looking For (talk) 22:23, 5 July 2020 (UTC)
- Randall writes “became infinite”, not “became infinity”, isn’t that a difference? Dividing by zero doesn’t give something finite, so it is in-finite, but not ∞, right?
The comic should not use the word "mortgage," because the calculations are based on sale price. The size of the mortgage depends on the down payment. Cellocgw (talk) 11:40, 2 July 2020 (UTC)
- My understanding is that if you fully mortgage your house (so that you now have in your hands enough money to buy the house again) and convert the total amount of money that the house is worth into oil, you can then fill your house with X feet of oil. 141.101.98.56 15:11, 2 July 2020 (UTC)
- Find me a mortgage that will give me 100% of the value of my house. Please! 162.158.123.155 04:02, 3 July 2020 (UTC)
- Hint: Start by not writing in the "Reason for mortgage" box anything like "I want to entirely fill my home with viscous and/or flammable liquid". Notwithstanding what I believe the US calls 'zoning laws'... 162.158.159.14 20:38, 3 July 2020 (UTC)
- Find me a mortgage that will give me 100% of the value of my house. Please! 162.158.123.155 04:02, 3 July 2020 (UTC)
It's a pity the graph doesn't go back as far as the 1973 oil crisis. 141.101.98.26 12:02, 3 July 2020 (UTC)
I belatedly wonder if the title is meant to be similar to some other famous Index that I happen to have not heard of. Searching around, Freedom House is an American... thing, which apparently publishes a "Freedom House Index" which is a sort of measurement of how "democratic" a country is from year to year. So something like that... Robert Carnegie [email protected] 162.158.159.14 21:25, 3 July 2020 (UTC)
Shouldn't the OHI be higher because the footprint of a multiple story house is less than its square footage? - 162.158.74.173
I sent this to Matt Levine, and he included it in his Money Stuff newsletter. [3] Benjaminikuta (talk) 07:01, 8 July 2020 (UTC)
