2042: Rolle's Theorem
| Rolle's Theorem |
 Title text: I mean, if it's that easy to get a theorem named for you ... "a straight line that passes through the center of a coplanar circle always divides the circle into two equal halves." Can I have that one? Wait, can I auction off the naming rights? It can be the Red Bull Theorem or the Quicken Loans Theorem, depending who wants it more. |
Explanation[edit]
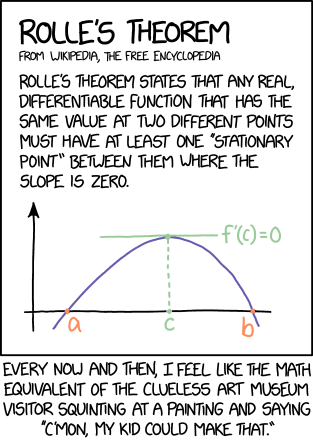
In mathematics, a differentiable function is a function that is "smooth" everywhere, without any sudden breaks or pointy "kinks" or similar. The derivative of such a function is a new function that represents the "slope" or "rate of change" of the original. The function in this comic curves up from point (a) until a point above (c), smoothly turns around, and then curves down from (c) to (b). As a result, the derivative of this function is positive from (a) to (c), and then is negative from (c) to (b). At (c) itself, the function is "flat": the more one zooms in, the more horizontal it looks. The function is moving neither up nor down, so the derivative is neither positive nor negative, but zero. This is what f'(c) = 0 means, as f' is a common notation for the derivative of the function f in differential calculus.
A theorem in mathematics is a statement that has been proven from former accepted statements, like other theorems or axioms. This comic references Rolle's theorem. The theorem essentially states that, if a smoothly changing function has the same output at two different inputs, then it must have one or more turning points in between, as the derivative is zero at each one. As a special case, should the function remain flat between the two inputs, then its derivative is actually zero for every point between the inputs. To Randall, this is obvious. However, the proof of this theorem is not as obvious as the result.
The seeming triviality of the theorem, coupled with the honour bestowed on the theorem namer, leads Randall to make a comparison to attendees of art museums who look at abstract art pieces and perceive only an apparent technical simplicity in the work. Such a visitor might exclaim "My child could paint that!". However, such works of art typically are seen as having value from attributes other than the painterly difficulty in achieving the piece. For example, an artist's work in this style may be lauded for its visionary qualities, or the emotions expressed through the choice of colours or textures. One such artist is Jackson Pollock. The 'clueless' visitor does not see these aspects and believes their child could imitate the piece. Randall suggests he experiences a similar feeling looking at Rolle's Theorem and noting only the obvious correctness without acknowledging the complicated nature of the proof, or other hidden aspects of the theorem.
In the title text, Randall mentions a line together with a coplanar circle. This simply means that both those two-dimensional objects must lay in the same plane in a higher, three-or-more-dimensional space. And by this means, every line drawn through the center of a circle is just a diameter which divides it into two equal parts. Even if this fact is trivial, even the legendary Proclus admits that the first man who proved it was Thales. Auctioning of naming rights, also noted in the title text, refers to the practice of naming entertainment venues for companies which pay for the privilege, such as any of the three Red Bull Arenas or Quicken Loans Arena. (See "Are there any theorems/objects involving company names." on r/math.) The naming of mathematical theorems (along with lemmas, equations, laws, methods, etc.) is not always straightforward and often results in misleading names.
Randall implies that there are many seemingly easy theorems like this. For instance the Dirichlet's box principle, also known as the Pigeonhole principle, which states that if you have more objects than containers, you're going to have to put at least two objects in one container.
Transcript[edit]
- [A single framed picture shows a colored x-y-graph with a text above:]
- Rolle's Theorem
- From Wikipedia, the free encyclopedia
- Rolle's theorem states that any real, differentiable function that has the same value at two different points must have at least one "stationary point" between them where the slope is zero.
- [The graph shows a sine like curve in blue intersecting the x-axis at points "a" and "b" marked in red while in the middle a point "c" has a vertical dashed green line to the apex and on top also in green f'(c)=0 is drawn with a horizontal tangent line.]
- [Caption below the frame:]
- Every now and then, I feel like the math equivalent of the clueless art museum visitor squinting at a painting and saying "c'mon, my kid could make that."
Discussion
Now we wait for https://en.wikipedia.org/wiki/Munroes_theorem. 172.69.54.165 15:51, 5 September 2018 (UTC)
- Can't wait to see how long it takes to remove the article. Linker (talk) 17:05, 5 September 2018 (UTC)
- Which article? The log is empty --172.69.151.94 09:06, 14 October 2023 (UTC)
- Don't you mean Munroe's theorem?Artem (talk) 06:35, 23 November 2025 (UTC)
- Proposed ideas for Munroe's Law:
- - Any seemingly simple idea will be difficult to prove; the simpler it seems, the harder the proof.
- - Any proof which is discovered by a layperson will have been previously discovered by an expert (or an "expert") in the field.
- Raj-a-Kiit (talk) 17:57, 5 September 2018 (UTC)
- I do not have the time to do it good, so here a suggestion: Would someone go to the wikipedia page of Rolle's theorem and add a "in popular culture" section? may be a first? Not even "Nash equilibrum" has that :-) 162.158.234.16 08:13, 6 September 2018 (UTC)
- Done. Kmote (talk) 17:56, 10 September 2018 (UTC)
- Speaking of popular culture, there's a (moderately) well known Ballad of Rolle's theorem Balada o vete Rolleovej ("moderately" meaning some people who studied at Faculty of mathematics in Bratislava might have heard (of) it) --Kventin (talk) 07:41, 7 September 2018 (UTC)
- Proposed idea for Munroe’s Law:
- – Whenever XKCD references a theorem, an edit war is caused on the respective Wikipedia article.--172.69.151.93 09:03, 14 October 2023 (UTC)
- I feel that can be generalized to "whenever xkcd references a Wikipedia article, an edit war is started on said article" guess who (if you want to | what i have done) 03:08, 25 September 2024 (UTC)
- – Whenever XKCD references a theorem, an edit war is caused on the respective Wikipedia article.--172.69.151.93 09:03, 14 October 2023 (UTC)
I feel like Euclid beat Randall to the punch here, a couple millennia. 162.158.155.146 16:54, 5 September 2018 (UTC)
I don't see that Thales has proven Randall's theorem. Do not to be confused with Thales's theorem, that's about right angles. Maybe I'm blind or just dumb, but if so it has to be explained with more traceable background. I just believe that this diagonal is so trivial that even the ancient Greeks weren't engaged on a proof. --Dgbrt (talk) 21:38, 5 September 2018 (UTC)
- From Wikipedia: Other quotes from Proclus list more of Thales' mathematical achievements: "They say that Thales was the first to demonstrate that the circle is bisected by the diameter, the cause of the bisection being the unimpeded passage of the straight line through the centre." Alexei Kopylov (talk) 05:39, 6 September 2018 (UTC)
- On the other hand not all historian believe Proclus. But van der Waerden does: [1]. Alexei Kopylov (talk) 05:49, 6 September 2018 (UTC)
Rolle's Theorem counterexample?
Isn't the TAN(x) function a counterexample to this? Starting at a given point, it rises to infinity, then returns from negative infinity to the same point without ever having a slope of zero. 172.68.58.89 06:58, 6 September 2018 (UTC)
- TAN(x) isn't differentiable at pi/2, hence the theorem doesn't apply--162.158.92.40 07:48, 6 September 2018 (UTC)
Clueless Museum Visitor
The math in the comic is well explained, but shouldn't there be something about the "math equivalent of the clueless art museum visitor..." part? -- Zetfr (talk) (please sign your comments with ~~~~) 09:17, 6 September 2018 (UTC)
- Seconded, all the argument here is about math that isn't even *in* the comic, whereas the bit that confuses me is the cultural metaphor... 162.158.154.235 07:16, 7 September 2018 (UTC)
- I had a go.162.158.154.103 08:35, 7 September 2018 (UTC)
Just so we're on the same page, while the proof of Rolle's theorem is not completely trivial, neither is it difficult by any means. Proving it seems to be a pretty common homework assignment in undergrad math classes, for example, so one might legitimately ask why it deserved to be named. Perhaps it's simply that it's old enough that the methods at the time were crappy, and so modern proofs are much easier. 172.69.22.140
- It is named because it's a very important theorem in calculus, used to prove many other theorems or results. So when you need to prove something using this property, instead of re-demonstrating it or merely saying "it is well known that..." (which often raises alarm bells in the mind of the reader/corrector), all you have to do is reference Rolle's theorem.162.158.155.158 11:08, 6 September 2018 (UTC)
- It could almost be called "Rolle's lemma". 162.158.154.103 12:28, 6 September 2018 (UTC)
- When I am teaching Rolle's theorem, I always make it a point to draw the link to reals. Rolle's theorem fails when the output is complex valued. Then you can see for yourself how non-trivial this is. 162.158.165.124 04:40, 7 September 2018 (UTC)
Has anyone else noted the irony of having a wiki page to explain a comic whose subject is how some things are self-evident? JamesCurran (talk) 20:13, 6 September 2018 (UTC)
Does the Kepler Conjecture actually belong on that list at the end? Most of the others are "derp" level intuitively obvious and/or essentially tautological on a very basic level, but the Kepler Conjecture couldn't actually be exhaustively proven until machine computation, nor is it intuitively definitive--if you've ever stacked round things into a box you've noticed that it feels like you're wasting a lot of space at the edges. So...? AtrumMessor (talk) 21:37, 6 September 2018 (UTC)
- I would also argue against most of the other examples. Neither the isoperimetric inequality nor the hairy ball theorem are obviously true and their proof is quite a bit more involved than the one of Rolle's theorem. The Jordan curve theorem sounds obvious but then the proof definitely isn't. The parallel postulate isn't even a theorem. The only real good example in the list is the pigeonhole principle.162.158.91.155 12:35, 7 September 2018 (UTC)
- I have removed all but that, as it is the only one comparable to Rolle's in simplicity to understand without understanding math. --Kynde (talk) 14:04, 7 September 2018 (UTC)
- I agree, Randall mentions nothing like that and a simple parallel is enough. --Dgbrt (talk) 14:25, 7 September 2018 (UTC)
- I would argue that a lot of them could have stayed. Just because some of the examples given do have a lot of "hidden" mathematical complexity and are important bases for mathematical fields does not mean they are not useful parallels to the comic's example. In fact, one that comes to mind is the infamous 300-page Russell/Whitehead proof of 1+1=2. If anything, the more axiomatically complex but intuitively, even stupidly obvious something is, the BETTER it fits. My original point was that the Kepler Conjecture felt like a "which one of these things is not like the others" situation in the original list, as it was not at all easily proven, nor is it intuitively obvious. Some of these were actually pretty useful examples and should have been left, no matter how foundational they are to calculus ;) AtrumMessor (talk) 06:46, 9 September 2018 (UTC)
I also suggest that Fundamental Theorem of Calculus be removed from this list. Firstly, the beginner student, just introduced to derivatives and antiderivatives, will not easily see that antiderivatives are the same as finding areas under curves. Instead, it is only obvious upon hindsight, after instruction. More importantly, a restriction of the FTC to better-behaved spaces shows a far greater insanity: the restricted FTC is a consequence of generalised Stokes's theorem applied twice. This operation is so highly unintuitive, that one simply cannot claim that this is in any way, shape, or form, trivial. I think that trying to pretend that anything in beginning calculus is obvious to students is just going to alienate them rather than soothe their worries. 162.158.165.124 04:40, 7 September 2018 (UTC)
- Ehh what? No, FTC restricted to smooth functions is simply a special-case of Stokes' Theorem. This is explained here. I don't even know what you could possibly mean by applying Stokes' theorem twice, in any context. Zmatt (talk) 13:23, 7 September 2018 (UTC)
- ``FTC restricted to smooth function is simply a special case of Stokes's theorem"" is basically what I said, although FTC proper applies to a wider range of functions. As to applying Stokes's theorem twice, remember that the differential form for areas is A = iint dw, where dw = dx ^ dy. You apply once to get that A = oint w, where oint runs around the entire boundary of the area to be considered. Then you have to use some smarts to zero the contributions from 3 of the 4 sides, leaving just the contribution from the x-axis. Then the boundary, which is supposed to have no boundary itself, gets two new boundaries, of which then you can apply another Stokes's theorem to get the F(b)-F(a) result. Again, this process is highly non-trivial, as evidenced by your failure to see what I meant from the first time talking about it. Pardon if the IP changed, it is me. 162.158.167.60 04:48, 9 September 2018 (UTC)
- No it isn't "basically" what you said. I know FTC applies to a wider range of functions, that's why I said "restricted to smooth functions". I have not even the slightest idea what process you're trying to explain or why you're talking about 2D integrals. FTC restricted to smooth functions is exactly Stokes restricted to a line-segment, there is no "process". Again, this wikipedia section explains this quite well, albeit informally. Zmatt (talk) 11:01, 10 September 2018 (UTC)
- You seem to be missing what I am referring to. There are at least two parts. Let's start with the main one. You keep referring to the same place of the same article. That is not under contention, so it is irrelevant. So I checked Wikipedia's article on FTC itself and I think I see why you don't see my point. When I learnt FTC from textbooks, the definition of integrals is via the area under curve, i.e. the relevant bit in the FTC article is the geometric intuition. The FTC article, however, quite much like you seem to be, however, only covers the anti-derivative part. In a sense, it comes down to the definition of what an ``integral" means. AFAIK, for beginners, there is only 3 definitions in common use, the directed area under curve, limit of a certain sum, and anti-derivatives. When I teach, I tend to define the directed area under curve, just because students like to see things. Because of that, my FTC has to cover the area under curve. And that is the 2D integral known to Leibniz. If you want the 2D integral, then you ought to integrate the fundamental differential form I was talking about---you don't talk about generalised Stokes's theorem without differential geometry, and I am trying to say that the identification of a definite integral with the area under curve is what is taught to beginning students, but is highly non-trivial under differential geometry! I hope this is clearer. Of course, the moment the 2D integral is reduced to a 1D integral with new boundaries, then the part you keep referring to is relevant, and again, not under any contention. I am simply saying I am not happy with that being the sole content of FTC. The FTC I respect is the one that includes the geometrical intuition. Finally, just the quibble---what part of my ``the restricted FTC is a consequence of generalised Stokes's theorem" is different from your ``FTC restricted to smooth functions is simply a special case of Stokes' theorem"? Even if you disagreed with my ``applied twice", you should not be disagreeing with my ``basically what I said". 162.158.166.191 16:55, 10 September 2018 (UTC)
"Munroe's theorem" should definitely refer to the circle thing in the alt text 162.158.62.57 (talk) 02:05, 7 September 2018 (UTC) (please sign your comments with ~~~~)
Since I'm half a mathematician, I did the math. I looked up Rolle's theorem and it uses the theorem of Weierstraß. I looked up the theorem of Weierstraß (better known as extreme value theorem) and it uses the theorem of Bolzano-Weierstraß. I looked up...why am I suddenly reminded of https://xkcd.com/609 ? :-) 141.101.104.71 08:36, 7 September 2018 (UTC)
What goes up must come down. 198.41.238.64 05:53, 8 September 2018 (UTC)
Going in the opposite direction.
Sure, some seemingly obvious things can be made theorems, but there's a point of view that the most complex theorems may seem obvious to a sufficiently smart entity, that we have such hard time studying mathematics simply because it's difficult for us to grasp long sequences of obvious connections in our insufficiently powerful imagination, so we need to break it down into manageable pieces. "I have come to believe, though very reluctantly, that it [mathematics] consists of tautologies. I fear that, to a mind of sufficient intellectual power, the whole of mathematics would appear trivial, as trivial as the statement that a four-legged animal is an animal." ---Bertrand Russell (1957) 162.158.74.231 (talk) 06:39, 11 September 2018 (UTC) (please sign your comments with ~~~~)
"This is what f'(c) = 0 means, as f' is a common notation for the derivative of the function f in differential calculus." Is it? I took both calculus and differential equations as an undergraduate (in the United States in the 1970s/1980s) and never saw that notation.Nitpicking (talk) 17:57, 1 August 2022 (UTC)
- Coming from a UK background, myself, I recognise it as such. Not really much experience the '70s, but definitely across the early '80s and beyond. For Secondary Education, in the first instance where the initial "Number machines" idea led straight into algebra, and differentiation/integration was in the second or third year (whatever that is in 'K-12'-style numbering that's in use today, seemingly imported from the US). Not sure what system dominated beyond secondary and tertiary/college levels and into my own university years (heading towards the '90s). It might have depended on whether it was the physics or the maths lectures and workshops (or indeed the given lecturer/workshopper of the moment) as to which of the many possible conventions we could have used and be considered correct. dFoo/dBar probably was used a lot, but obviously got messier than functioning things when going far into that sort of thing (either direction!). Though whether curly-ds or primes, it does get more difficult to differentiate the number of differentiations once you get into higher realms of notation... ;)
- I went a-looking and it is fairly common, even unto higher derivatives with multiple marks (which I've used, well... to no more than the third degree, probably).
- Looking further still, I now know (have reminded myself?) that it's 'Lagrangian' notation, at least as far as it stays unawkward before going into the numeric form rather than repeated Prime-marks towards a sublime ridiculousness.
- Of course, elsewhere on that latter link you might find your own learnt system. Or various others more familiar to you and which I may as readily recognise, unprompted. 162.158.159.133 18:23, 1 August 2022 (UTC)
 Add comment
Add comment
