2599: Spacecraft Debris Odds Ratio
Explanation
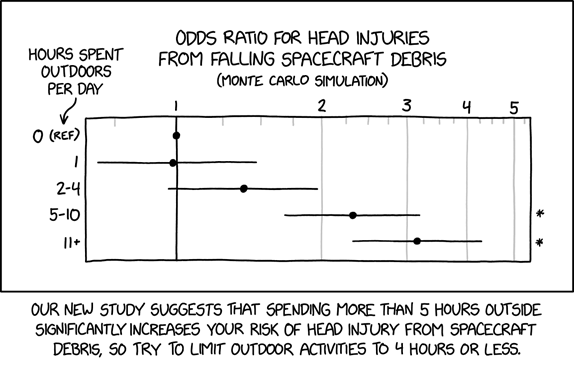
This comic is a misunderstanding of statistics very similar to that of 1252: Increased Risk. It explains that going outside for more than 5 hours per day significantly increases your risk of head injury from falling spacecraft, and advises to limit outside activity to avoid this risk.
However, since the odds of being hit in the head by (any part of) a falling spacecraft are astronomically low to begin with, quadrupling it or more still results in a negligible probability. The horizontal error bars for times greater than 4 hours are marked with asterisks to indicate they are significantly different from the reference value at 0 hours, as indeed those error bars don't overlap the vertical line for the 0-hours reference value.
Error bars are graphical representations of the variability of data and used on graphs to indicate the error or uncertainty in a reported measurement.
Presenting the data by hour brackets hides the data distribution inside each bracket. If the data were presented hour by hour, and not by groups of hours, they may show a different threshold of increased risk or no threshold (odds ratio could be linear).
The graph and error bars are based on a Monte Carlo simulation, a type of computational algorithm that uses repeated random sampling to obtain the likelihood of a range of results of occurring; see, for instance, this article about Monte Carlo simulations. Additionally, this may indicate that the entire study was conducted via a Monte Carlo simulation and that no real data was collected adding to the absurdity of the claim that more time spent outside could lead to an increased risk of head injuries due to falling space craft. Indeed, it is so rare for humans to be struck by spacecraft debris that a simulation is probably the only way to study the risk; an absurdly large sample size, involving tens of millions of participants over several decades, would be necessary to obtain significant experimental data.
The specific reference to falling spacecraft is likely inspired by events happening around the time of this comics release (March 2022). Around a month before this was posted, the head of the Russian space agency, Roscosmos, warned that sanctions against Russia (mostly those over the 2022 Russian invasion of Ukraine) could result in the International Space Station crashing. Since the Russian section of the space station is the one that provides propulsion (although it is built to rely on the power generated by the other sections), this was taken seriously and as of when this was posted, NASA was trying to come up with alternative stabilization strategies in case the situation worsened. There was also a recent report of some 600 kg space rocket debris found in Brazil.
The title text makes a similar joke. While the increase in chances of death by a bear attack are greater when going outside than the decrease in chances of death by cardiovascular disease, by getting out to exercise, it is incorrect to combine them in this way, since cardiovascular disease has a much higher starting chance of death, and reducing it by 30% has a much more significant effect on overall life expectancy than quadrupling the very very small chance of death by bear attack. At least for the majority of us who don't live in or near wild bears' natural habitats.
The "280% increase" of the title text is also an error, though perhaps not for reasons that are obvious at first (for instance, the correct calculation is not "300% − 30% = 270%"). To "increase by 300%" means multiplying the probability by (1 + 3.0) = 4.0, while to "decrease by 30%" means multiplying by (1 − 0.3) = 0.7. Combining these means multiplying by both, for an overall change of 4.0 × 0.7 = 2.8, or 280%. However, this result means the risk has increased to 280% of its old value, not by 280%. And in any case, it is still not valid to simply combine two changes in wildly different risks like this.
Odds & Odds Ratios
The odds of an event is the probability that it happens divided by the probability that it doesn't happen. People often express odds as a ratio (e.g. the odds of rolling a 6 on a 6-sided dice might be expressed as 0.16777... : 0.83333..., or equivalently as 1:5), but it is important to note that such ratios are not odds ratios (it would be fitting to call this a "probability ratio", but this terminology is not standard).
An odds ratio is the odds of event O happening, given that some other event E has occurred, divided by the odds of O given that E has not occurred. O is sometimes called an "outcome" and E is sometimes called an "exposure", because people are often interested in comparing things like the odds of getting lung cancer (O) given that you smoke (E) to the odds of getting lung cancer given that you don't smoke, as a way of measuring the extent to which exposure to E influences outcome O. In the case of the comic, the outcome variable O is the event of getting a head injury from falling spacecraft debris, and the exposure variable E is the event of spending H hours per day outside, for various values of H. The comic appears to be saying that for each value of H, there are two options for E: either you spend H hours per day outside or you never go outside.
So for small values of H (e.g. 1 hour per day), the comic is saying that the event of being hit by spacecraft debris is more or less independent of the event of spending H hours per day outside, which is to say that the odds of being hit is more or less the same regardless of the choice you make between spending H hours per day outside and never going outside. Hence the dot on the 1-hour bar is close to 1, because the two odds are more or less equal (the dot appears to represent an average estimate of the odds ratio).
Note that when calculating the odds ratios for this comic, the odds in the denominators are always the same, as they are the odds of being hit given that you never go outside, which does not depend on H. So when the comic says that the odds ratio is above 3 for H={11+ hours per day}, it is effectively saying that the odds of being hit when you spend this much time outside is a bit more than 3 times the odds of being hit when you spend 1 hour per day outside.
Suppose the probability of being hit is: P when you spend 1 hour per day outside, and Q when you spend 11+ hours per day outside. The odds of being hit under these two exposures are P/(1-P) and Q/(1-Q) respectively, and because the odds ratios have equal denominators, the comic is saying that Q/(1-Q) = kP/(1-P), where k is a bit more than 3. If we rearrange this to get an expression for Q, we get:
Q/(1-Q) = kP/(1-P)
<=> Q(1-P) = kP(1-Q)
<=> Q-QP = kP-kPQ
<=> Q+kPQ-QP = kP
<=> Q(1+kP-P) = kP
<=> Q = kP/(1+kP-P)
<=> Q = P/(P+(1-P)/k) {by dividing the numerator and denominator by k}
As P is negligibly small, 1-P is very close to 1, and P+(1-P)/k is very close to 1/k. Thus Q is very close to kP (i.e. a bit more than 3 times P), meaning that the probability of being hit when you spend 11+ hours per day outside is still negligibly small. Thus, the comic's suggestion that we spend 4 hours or less outside based on the estimated odds ratios is extremely misguided.
Transcript
- [A chart is shown. Above the chart there is a heading, with a subheading below it:]
- Odds ratio for head injuries from falling spacecraft debris
- (Monte Carlo Simulation)
- [The chart is rectangular with the X-axis labels above the chart with numbers from 1 to 5. These are places over vertical lines. The first at 1 is black, the other four are light gray. There are three smaller light gray ticks between each set of lines, and one on either side of the first and last. The distance between lines gets smaller and smaller towards the right, probably logarithmic.]
- X-axis: 1 2 3 4 5
- [The Y-axis is not scaled; there are no ticks or lines. Instead it just gives five labels from top to bottom. Above those labels there is an arrow pointing to the top one with a label above explaning the axis.]
- Hours spent outdoors per day
- Y-axis:
- 0 (ref)
- 1
- 2-4
- 5-10
- 11+
- [Aligned with each of these five divisions of the Y-axis there is a dot. The top one is placed on the solid line under 1 as a reference point. The other four dots all have long error bars, with the dots at the center of these. The second dot is a bit to the left of the solid line, with the error bar going almost to the left edge of the graph and halfway to the first light gray line to the right. The third dot is located halfway between the solid and the first light gray line with the error bar just crossing the solid line, and almost reaching the gray line. The fourth dot is about a third way between the first and second of the gray lines, with the error bar crossing both these lines. The fifth and last dot is just past the second gray line, with the error bar crossing both that, going more than half toward the first gray line, and also just past the third gray line. On the same height as the two bottom dots, there are asterisks just right of the edge of the graph.]
- *
- *
- [Below the panel there is a caption:]
- Our new study suggests that spending more than 5 hours outside significantly increases your risk of head injury from spacecraft debris, so try to limit outdoor activities to 4 hours or less.
Trivia
- In the original version of the comic the Y-axis label referred to "hours spent outdoors". So more than four hours spent outdoors in one's lifetime would be a problem.
- But later the comic was edited to specify "hours spent outdoors per day", which makes more sense.
- When the new version was uploaded, Randall again made the error of making the two versions of the comic image the same size, as he did earlier in 2576: Control Group, see that comic's trivia
- This resulted in the problem that the comic broke the boundaries on the xkcd website.
- This comic's title text has a typo in the sentence "That's a 280% increased".
Discussion
correct me if i'm wrong, but i believe 300 - 30 is 270, not 280? 172.68.50.85 22:50, 28 March 2022 (UTC)
- something something percentage points maybe? idk 172.70.134.91 22:56, 28 March 2022 (UTC)Bumpf
- Most likely there is an unstated chance of death by not going outside... presumably ~10% but there's no way to know the breakdown (could be nearly all cardio, could be nearly all ursine if they live in a cave next bears) 172.69.70.127 23:02, 28 March 2022 (UTC)
- 300% increase is multiplying by (1+3), 30% decrease is multiplying by (1-0.3) , %increases are multiplicative so the increase is by a factor of 4*0.7=2.8, which is 280% of the original value (or a 180% increase). 162.158.146.69 (talk) (please sign your comments with ~~~~)
- Yeah, barring a total mistake, that must be where the number came from, but it seems odd by the inconsistent way it is expressed, as it assumes the 300% increase for the bear attack is added to the initial value for a final amount of 400%, along with a similar treatment for the 30% decrease, but the 280% is simply the final value skipping past that step to the conclusion afterwards that is not even shown for the previous numbers. But with the improper grammar, if it's not an actual typo, it may be trying to show the speaker acting dumb or irrational, as it doesn't make sense to end with "increased" instead of "increase" without changing part of the words before that number. Someone thinking that poorly though likely wouldn't be able to multiply things properly to produce that 280% number though.--172.70.130.153 01:13, 29 March 2022 (UTC)
- Joke proof: Assume that every year 400 people are killed by bears in the world, of which 100 are killed inside and 300 are killed outside. Then, indeed, by going outside, the probability that you will be killed by bears increases from 100 to 300: that is 300%. On the other hand, we know that walking outside every day will reduce your risk of death from cardiovascular disease by 30%. Therefore, by walking outside properly, 30% of the above-mentioned 400 people, i.e. 120 people, could in theory avoid death from the said disease, if not attacked by bears. This implies that, even if everyone in the world walked outside every day, only 120 out of the 400 bear attack victims would be potentially saved, while 280 would die anyway. Since by hypothesis only 100 are killed inside by bear attacks, going outside will clearly increase the probability of deadly bear attacks, from 100 to 280: that is 280%. —Yosei (talk) 09:52, 29 March 2022 (UTC)
- As said above, 300% increase and 30% decrease gives a factor ×2.8 which is a +180% increase (not 280%) 162.158.50.176 10:38, 29 March 2022 (UTC)
- It's a joke :) Since the title text is obviously a joke, maybe we shouldn't over-analyze it, except we can enjoy ourselves by “analyzing” it half-jokingly. Seriously, though, there is also some ambiguity in a natural language itself: e.g. by “one-and-a-half times larger than”, one may mean “one-and-a-half times as large as” (150%), or one may mean “150% larger than” (250%). When spoken informally, this kind of ambiguity is not uncommon. Another example would be “five hundred one thousandths” which may mean 501/1000 or 500/1000. Take it easy & take care :) — Yosei (talk) 11:38, 29 March 2022 (UTC)
- This is what I love about XKCD, the jokes come with proofs. Does it depend on what order you apply them in? If you decrease the risk by 30%, you have 70%, then increase it by 300%, you get... 210%? Or 270%? Percentage points vs. percent again isn't it. Why is life so complicated? --192·168·0·1 (talk) 12:46, 29 March 2022 (UTC)
- 300% increase is multiplying by (1+3), 30% decrease is multiplying by (1-0.3) , %increases are multiplicative so the increase is by a factor of 4*0.7=2.8, which is 280% of the original value (or a 180% increase). 162.158.146.69 (talk) (please sign your comments with ~~~~)
- It doesn't really matter because the whole thing is complete nonsense. You can't combine the risks unless you know how big they are relative to each other. Let's say 1,000 people stay inside. 2 are killed by a bear and 10 die of cardiovascular disease - 12 people in total. With the given percentage changes, of 1,000 people who go outside, 8 get killed by bears (300% increase) and 7 die of heart disease (30% decrease), a total of 15. It's more dangerous to go outside than stay in. However, if 250 of the people who stay inside die of heart disease, then we have 252 deaths in total for staying in and only 175+8=183 for going out Jeremyp (talk) 15:33, 29 March 2022 (UTC).
"That's a 280% increased" has a typo/grammaro. The last word should be "increase". Barmar (talk) 23:04, 28 March 2022 (UTC)
- I think the actual typo is the "a" so should be "That's 280% increased" 162.158.146.69 (talk) (please sign your comments with ~~~~)
- In standard American grammar it is much more likely that he meant "That's a 280% increase" than "That's 280% increased." You might say the odds ratio that he meant the former over the latter is 3+.162.158.166.87 15:46, 29 March 2022 (UTC)
Also what's an odds ratio?? ~~Bumpf 172.70.38.41 (talk) (please sign your comments with ~~~~)
- I assume something like "million to one". But the units of the horizontal axis clearly don't correspond to that. I don't know what those units are, they're not a percentage, either. Barmar (talk) 00:40, 29 March 2022 (UTC)
- if you say "this is 4 times as likely" then "4" is the "odds ratio", this is the type of number appearing on the horizontal axis 162.158.146.69 (talk) (please sign your comments with ~~~~)
- An odds-ratio is a way of reporting the results for predictions of binary outcomes. It's a transformation of the (not easily interpretable) regression coefficient. For example, if the OR for "males" (vs females) is "0.70", they're 70% as likely to have the outcome as females; if it's "1.32", then males are 1.32x as likely (equivalently: 32% more likely) to have that outcome as females. 108.162.249.75 Gye Greene
Did something happen to the size of the image after the initial posting? Barmar (talk) 00:40, 29 March 2022 (UTC)
What's with the asterisks on the right side? Jordan Brown (talk) 00:50, 29 March 2022 (UTC)
- I think the asterisks denote that the value at this range is "significant" because its error bars do not overlap with the baseline. If you stay outdoors 5 hours or more in a day, there is a nonzero chance that you will be hit by flying space debris. Laura (talk) 08:15, 29 March 2022 (UTC)
There should probably be an explanation of what "Monte Carlo Simulation" means, as many people who would actually want an explanation of this strip would likely be unfamiliar with that term.--172.70.131.122 01:02, 29 March 2022 (UTC)
- Yes, exactly! I got as far as finding Monte Carlo method via a redirect but have no idea how the bars are supposed to work, what the reference point is supposed to mean, or why the columns get skinnier toward the right. Not dumb, but next to no statistics education. Yngvadottir (talk) 07:51, 29 March 2022 (UTC)
Why is the x-axis of the chart in logarithmic spacing? Any particular reason for this, or is it part of the joke? Captain Nemo (talk) 09:29, 29 March 2022 (UTC)
I wonder if it's deliberate that there's actually less risk if you go outside 1 hour per day. --192·168·0·1 (talk) 12:46, 29 March 2022 (UTC)
Is this covid commentary? Like how everyone got freaked about the odds for covid to the point where they stopped exercising and shutting everyone inside and degrading their mental health? 172.70.131.122 18:26, 29 March 2022 (UTC)
- Odds ratio confusion?
I am very confused by the X axis of this comic, I feel like I must be misunderstanding how this works, but I thought I understood how odds ratios worked. Maybe not. The graph "reads" that "In the reference situation, with zero hours spent outside, the odds ratio for head injuries from falling spacecraft debris is 1.0 ± 0." A 1.0 odds ratio means 1.0:1.0, or that either possibility is 50% likely. That is, there's an even chance your head will be injured by spacecraft debris or that it will not, if you stay indoors. That does not seem like it could be right, so can someone point me to my error? Thanks! JohnHawkinson (talk) 09:34, 29 March 2022 (UTC)
- As best I can tell, this is taking odds as a ratio between any two events. Rather than the usual "success : failure" (or "happens : doesn't happen"), it's "this scenario happens : control scenario happens". By definition, the control scenario is set at 1.0, and something at a ratio of (say) 2.0 is twice as likely to happen. -- Peregrine (talk) 10:50, 29 March 2022 (UTC)
- I definitely think we need to put something explaining what an odds ratio is. But since I feel the need to have it explained, I'm not going to be the one to explain it. --192·168·0·1 (talk) 12:46, 29 March 2022 (UTC)
- I've added an "Odds & Odds Ratios" section to the comic. Does it clear things up? MelodiousThunk (talk) 16:00, 30 March 2022 (UTC)
- I definitely think we need to put something explaining what an odds ratio is. But since I feel the need to have it explained, I'm not going to be the one to explain it. --192·168·0·1 (talk) 12:46, 29 March 2022 (UTC)
- If the guess is correct about the subject being that a possible surprise action by Russia could drop the International Space Station on our heads, or even just its Starlink dish, I think that whether you're indoors or outdoors when its orbit intersects with your coordinates won't affect the risk of head injury. I cannot tell if that's what the chart claims to say. Robert Carnegie [email protected] 172.70.90.145 23:58, 30 March 2022 (UTC)
- Per day
Looks like the comic has been updated to clarify that the number of hours is per day. I'll leave it to someone more experienced with this website to update it, but in any case it makes the note "It is very difficult to avoid being outside for more than four hours in a total lifetime" moot. 172.70.114.147 12:31, 29 March 2022 (UTC)
- I uploaded the new version that includes "per day" in the y-axis label. But the image size also changed, now the image is the normal _2x size. I'm hoping that will get fixed eventually, like it did for 2576: Control Group. Orion205 (talk) 22:42, 29 March 2022 (UTC)
- Monte Carlo Tree Searches
MCTSs are one of those things that don't seem like they should work but they do Beanie talk 20:55, 29 March 2022 (UTC)
- I just did my own Monte Carlo Tree Search and... there's definitely at least one, jutting up into the bottom/right of that overview. :-p 172.70.91.36 22:37, 29 March 2022 (UTC)
- Image scaling off
Does anyone else experience a problem with the scaling of the comic image? It is not fitting to the frame, but displays on full size on the web page. It only happens for this comic, not other ones, and i see it both on the main page as the xkcd/2599 page. Some mistake for sure, but I have not seen this before. Screenshot proof: imgur link Flekkie (talk) 22:32, 29 March 2022 (UTC)
- This happened back in 2576: Control Group. It was fixed after about a week. Orion205 (talk) 22:42, 29 March 2022 (UTC)
The error with the really big image is still present for me. 172.69.90.77 14:24, 30 March 2022 (UTC)
x-axis of the chart in logarithmic spacing
First timer here, please forgive me if a new discussion subject is inappropriate for the x-axis of the chart being in logarithmic spacing, but I think this warrants considerable discussion by itself (a) because it is a major visual element of the comic, (b) it has received only brief attention to date in explainxkcd discussion.
My thoughts:
I am not a statistician. Odds ratios in medicine are usually expressed in a linear manner. Thus, the logarithmic scale for the x-axis is curious. But given the underlying probability of being hit by space debris approaches an asymptote of a near-zero actual probability, perhaps a logarithmic scale is simply correct? It is clearly a deliberate design element, and one that is a major part of the comic.
So those more skilled in stats and explaining xkcd humor will add a few sentences on this matter to the main description! Speculation - perhaps logarithmic is "accurate" within the nonsense assumptions, and so there for consistency? Or perhaps it is a deliberate (by Randall) additional "error" (by the supposed "authors" of the study), and thus the presence of a logarithmic scale compounds the nonsense, as it were, exponentially?
- Linear correlation?
I'm wondering how the correlation between time spent outside and chance of getting hit could be anything other than linear. If 1 hour outside gives you X probability, surely 2 hours outside would be 2*X probability. FishDawg (talk) 05:37, 7 April 2022 (UTC)
- Sort of, but probabilities don't exactly behave like that. On that analysis, given enough time outside, the probability would pass 1 and keep on rising. But a probability of 1 is absolute certainty, so probabilities higher than that are meaningless. I believe the comic is consistent with your assumption that the rate is constant -- the probability of getting hit during an hour is the same no matter which hour it is. It seems reasonable to me, too. Then after 1 hour, your probability of remaining unhit is 0.999999999 or whatever. After 2 hours, it's the probability of remaining unhit in the first hour times the probability of remaining unhit in the second hour, 0.999999999^2. After 3 hours, it's 0.999999999^3, and so on. So the probability of *ever* getting hit actually follows an exponential curve. 108.162.245.173 16:32, 8 April 2022 (UTC)
- (I mean, the rate might not be constant not on a time scale of decades or more. You could go from a society that can't launch spacecraft at all to launching a few and then many, or from a society that just lets 'em fall to one that takes responsibility for moving large pieces into a parking orbit or a controlled deorbit, or from a society that takes responsibility to a charred ruin pocked with circles of radioactive glass, or from that to the rise of Atlantean mages from the tunnels of Shambhala whose mana shall deorbit all things, as the History Channel hath prophesied. But anyway.) 108.162.245.173 16:33, 8 April 2022 (UTC)
So much confusion about the comic and the explanation read like a bunch of individual comments on top of each other. I took the liberty of rewriting the whole thing (actually, I just wanted to explain Monte Carlo simulations better but then things escalated). I'm fairly certain that I understand the joke of the comic - Randall was simply cramming as much misuse of statistical methods as possible into one "study". The explanation is now rewritten in a pattern of "method->what method is used for->how it's misleading here". I'm still not happy with all the details, but I hope the explanation as a whole makes more sense now and that I managed to write understandably. Rebekka (talk) 05:27, 1 July 2023 (UTC)