2821: Path Minimization

|< < Prev Comic #2821 (August 28, 2023) Next > >|

Path Minimization

Title text: Of course you get an ice cream cone for the swimmer too! You're not a monster.

Explanation

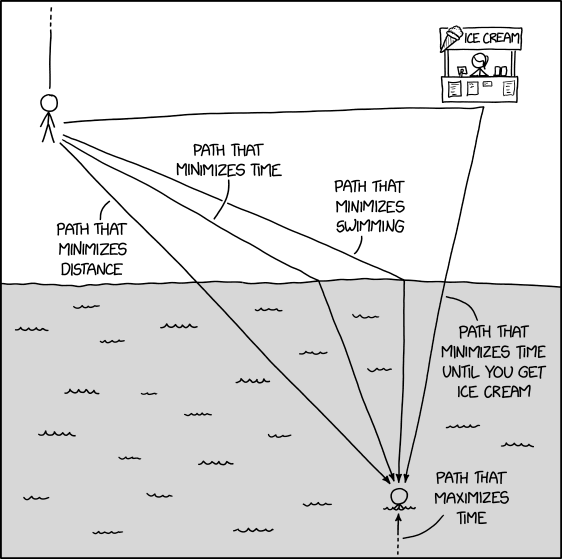
In this comic, it appears that Cueball, standing on shore, is observing a swimmer who is possibly (but not obviously) in distress. The comic illustrates five potential paths that can be taken to reach the swimmer, each with a different reason to make them viable, in the manner of demonstrating different optimal strategies that can be chosen.

The first path is a direct line from Cueball, straight to the swimmer, which allows for the minimum possible distance to be traveled, some on land and the remainder in the water.

The second path travels more obliquely from Cueball to the water and then at a sharper angle to the swimmer. This path would take the shortest amount of time, presuming that Cueball would move faster on land (covering more of the distance) and slower through the water (but less distance). The exact angles would depend on how much faster Cueball is on land than in the water. The relationship between speeds and angles is the same as that in Snell's law for light passing between two media.

The third path travels at a far more oblique angle to the water, such that the subsequent swimming path is entirely perpendicular to the shoreline, adding to the amount of time spent on land in order to minimize the time spent swimming. Depending on one's swimming ability versus running ability, this could be the safest path to take. It might also be more sensible to keep the target in clear sight for as long as possible, from the land, then aim exactly away from shore when both your head and theirs are barely at wave-height (though currents may complicate this). But this is a completely different reason from the distance or time preferences.

The fourth path travels nearly parallel to the beach. In fact moving slightly away from the swimmer but towards an intermediate goal: an ice cream stand. After that, the path turns and aims straight towards the swimmer, as all the others eventually do (although it is not made clear at this point if Cueball will spend time eating his ice cream on the beach, or will attempt to carry and possibly eat an ice cream whilst swimming).

The fifth and final path, barely recognizable as a path, points off the top of the comic and reappears at the bottom. This path presumably travels around the entire world, likely stopping for many, many rest breaks. It is labeled as the path that maximizes time. It should be noted that, by the definition given, it is theoretically possible to stretch the maximum time taken out forever by simply walking away and never returning.

You could also fulfill the criteria of reaching the target in finite, but arbitrarily long, time by following a random walk(+swim) or even follow a space-filling curve carefully chosen to be the maximally finite scenario. Or you could simply choose any path, and stop for an arbitrarily long time, or travel at a speed approaching zero. In the comic, however, a requirement for simplicity of path may dictate the use of something close to the opposing great-circle distance, or a variation that has a maximal swim-time even without undue time-wasting detours, and assume equal speeds of travel on all routes.

Alternatively, the fifth path may be a joke playing on relativity. In special and general relativity, timelike geodesics (locally) maximize the proper time between spacetime events. In a spacetime diagram (in sufficiently nice coordinates), an upwards-directed vertical line would be such a geodesic. Under this interpretation, the fifth path isn't a path around the world or through space at all, but through spacetime.

The comic pokes fun at two famous physical/mathematical problems that are usually stated as happening on a beach. The first is the Lifeguard problem, which Richard Feynman, in his book QED, uses to illustrate Fermat's principle, or principle of least time, which states that the path taken by a light ray between two given points is the path that can be traveled in the least time. This is closely related to Stationary-action principle for mechanical systems. In Feynman's words:

"Finding the path of least time for light is like finding the path of least time for a lifeguard running and then swimming to rescue a drowning victim: the path of least distance has too much water in it; the path of least water has too much sand in it; the path of least time is a compromise between the two." - Richard Feynman, QED - The Strange Theory of Light and Matter (1988, Princeton University Press), Chapter 2.

It is also possible that the comic makes fun of Feynman's idea that a photon (Cueball) would take every path to reach its destination, including the one that goes around the Earth, so that the paths shown are all being taken instead of being options Cueball is considering (therefore he could bring an ice cream to the swimmer).

The second problem referenced in this comic is the Beach Vendor Problem, which is stated as follows. Suppose that on a long beach there are two ice cream vendors. Customers are uniformly distributed on the beach and each person will go get the ice cream at the closest vendor. Each vendor wants to maximize the number of customers that buy at their place. To minimize the customer's walking time, the optimal configuration would be to have one vendor at 1/4 of the beach length and the other at 3/4, but Hotelling's law predicts that the two shops will converge to the middle of the beach, in an attempt to steal as many customers as possible from the competition. This is a case of Nash equilibrium that is also related to the Median voter theorem. If the number of vendors is larger than 2, the problem may become considerably more complicated.

The title text adds to the ice-cream path the stipulation that you also carry an ice-cream to the target swimmer to 'justify' that choice of route. But how this squares with the reason to rendezvous with the swimmer, or the manner in which this would further complicate the swimming stage, goes unsaid. But it makes it clear that not doing this isn't considered socially permissible, whether or not he had stopped to eat an ice-cream of his own beforehand.

Transcript

This transcript is incomplete. Please help editing it! Thanks.

[Cueball stands on the beach, with another person in the water. Ponytail stands on the beach in an ice cream stand in the top right corner.]

Path that minimizes distance [A straight line from beach cueball to ocean cueball, bearing about 135]

Path that minimizes time [A line from beach cueball to the waterline closer to horizontal, bearing about 120, then angling towards ocean cueball, bearing about 150]

Path that minimizes swimming [A line from beach cueball to the waterline closest to ocean cueball, bearing about 115, then angling toward ocean cueball, bearing 180]

Path that minimizes time until you get ice cream [A line from beach cueball to the ice cream stand manned by Ponytail, bearing about 90, then angling toward ocean cueball, bearing about 190]

Path that maximizes time [A line from beach cueball away from the shore, bearing 0, fading and disappearing at the top of the panel, and reappearing at the bottom of the panel directly below ocean cueball]

 add a comment! ⋅  add a topic (use sparingly)! ⋅  refresh comments!

Discussion

Judging from the angle of the arms, I do not believe that the swimmer is in distress. In fact I think the swimmer is just a future projection of Cueball, not a separate person.

I agree that the swimmer does not appear to be in distress, although the title text suggests that it is probably a separate person.

My personal interpretation is that the situation is "meeting a friend at the beach to get ice cream". Options are either a) meet the friend first and then swim back to get ice cream or b) get ice cream first and take it out to eat together in the water. 172.70.86.54 04:02, 29 August 2023 (UTC)

Or the more sensible walk to the water's edge and wait for your friend to swim in to meet you... 172.70.85.29 08:43, 29 August 2023 (UTC)

I agree as well, I changed it to "possibly in distress". Barmar (talk) 04:43, 29 August 2023 (UTC)

I changed it further. Still admits the possibility, but less possibly than "possibly" hints at. (It is, nonetheless, a (mostly!) typical "you need to get here, minimising <some form of time/distance/energy/endurance resource>, what is the optimal strategy" tbing that lifesaving courses might include to train you in such considerations. 172.71.242.82 09:01, 29 August 2023 (UTC)

Technically, the path that minimizes swimming passed a nearby boat rental stand. (by the way, I didn't write the unsigned paragraph above this one) 172.69.247.40 03:05, 29 August 2023 (UTC)

When I first saw the comic, I thought cueball was suspended on a tether in the air above the water, and the ice cream stand was floating. I didn't realize it was a beach until I read this explanation. Barmar (talk) 04:41, 29 August 2023 (UTC)

Me too! Instead of a tether I thought cueball was free falling into the water with a desire to get to the end state (the swimmer), and the ice cream stand was free falling as well.V-squared (talk) 01:44, 30 August 2023 (UTC)

The ice cream path reminds me of the bread-first search (similar punchline). 172.71.182.158 06:55, 29 August 2023 (UTC)

Noting, in passing, that an almost "flosbury flop"-like path could have been shown, too. A gentle curve, bending to hit the shore somewhere between shortest-time and shortest-swim, that would allow maximum run-up to dive into the water at the right angle to then power straight towards the target with the original running impetus turned straight into initial swimming speed, with no sharp turns involved. (Also, an 'Aquaman' line, perhaps exactly complimentary to the land-favouring 'bent-leg' routes, minimising/reducing land in favour of water.) 172.71.242.82

Note that for Aquaman, the line minimizing land would be the fastest. He swims very fast. -- Hkmaly (talk) 21:45, 29 August 2023 (UTC)

This was one of my first edits in this wiki, so I hope I didn't do anything wrong. I think this comic clearly references Feynman's Lifeguard problem (there is an almost identical diagram in his QED book) and the Ice-cream vendor problem. I wrote a couple of paragraphs explaining this, but they were promptly deleted by the next editor. Did I do something wrong? I think the explanation is incomplete without those references. Prallax (talk) 10:08, 29 August 2023 (UTC)

Seeing the history, this is probably just an edit conflict, you should insert your contribution again. Cochonou (talk) 11:54, 29 August 2023 (UTC)

It looks like it was my edit that 'overwrit' Prallax's. Though I got no "edit conflict" notification (or I'd have at least tried to reintegrate my failed changes into the revised 'current prior' version, or at least revisit the diffs to reinstate the best of what I'd caused to vanish/undo). Thinking back, it might have been due to a server time-out which meant I resubmitted, fooling the back end about what version I was (thinking I was) actually adding to/revising... I'm pretty sure it occasionally does that, and probably more than I ever know about, if I don't have reason to check the page histories in detail...

Anyway, recovered the paragraphs and re-added them to the end (maybe should have been inserted before the traditionally final title-text-paragraph?) on the original editor's behalf, as they looked fairly good and I didn't see anything in them that I might want to change (not even markup).

So both apologies and congratulations to their author! They might later get tweaked/redone, b6 others, but as far as ('one-of-my-')first-time edits go I'd have personally been proud to have done as well, whatever my first (probably disasterous) edits might actually have been, oh so many years ago and lost in the mists of anonymous-IPdom... Keep it up, and welcome to the rabble! ;) 172.70.91.8 12:45, 29 August 2023 (UTC)

Thank you for reverting and fixing this! I'm moving it before the paragraph about the title text as suggested. Prallax (talk) 21:14, 29 August 2023 (UTC)

Reminds me of https://xkcd.com/85/ Betamaj (talk) 12:06, 29 August 2023 (UTC)

One of the first comments there mentions trying to reach a drowning swimmer. Barmar (talk) 14:14, 29 August 2023 (UTC)

I was going to complain about reruns, but the addition of ice-cream has sweetened the deal. ProphetZarquon (talk) 16:51, 30 August 2023 (UTC)

I don't know if I agree with the Beach Vendor paragraph. There's only one vendor, and there's no reason for an ice cream stand on a beach to be a reference to the problem. (Ice cream stands on beaches are pretty common, at least near I live.) DownGoer (talk) 12:50, 29 August 2023 (UTC)

I question the first-paragraph comment about how the paths are "indicative of the path light takes between materials with different refractive indices". That applies to only 2 of the 5 paths. BunsenH (talk) 15:48, 29 August 2023 (UTC)

Arguably just the one (extremely exotic materials aside) if you don't count the straight-there path (zero difference). But it is relevent to quote how the "optimal speed route" is equivalent to a refractive-path (for similar underlying mathematics) as an analogue, which is further down. 172.70.90.232 18:20, 29 August 2023 (UTC)

Noone is going to comment how hard would be to swim with one, not speaking about two, ice creams? -- Hkmaly (talk) 21:45, 29 August 2023 (UTC)

Instead of the ice-cream cone, one should perhaps go for a float! ;) 172.70.85.214 21:52, 29 August 2023 (UTC)

These talk sections are worth scrolling though just to find the perfect dad joke. You, my friend, did not disappoint. Trogdor147 (talk) 01:31, 30 August 2023 (UTC)

Actually, there is no real path that maximizes time; you can always increase time by taking another detour. --172.70.246.119 06:36, 30 August 2023 (UTC)

In my case, every path I take is chosen to minimize the time until I get ice cream. I've got ice cream right now, so I feel like I could go anywhere! ProphetZarquon (talk) 16:58, 30 August 2023 (UTC)

I hope the swimmer beats Cueball to the Ice Cream vendor to get the last ice cream. If only there was a mathematical process to work out who would get there first? Kev (talk) 22:11, 30 August 2023 (UTC)

I suppose the angles here could be used to find the ratio of Cueball's walk speed vs swim speed? Though perhaps it ends up being a function of how long the lengths are. I've been away from math too long, I guess. --172.68.150.83 22:34, 30 August 2023 (UTC)

Incidence angle is 61.4° while refraction angle is 21.2°, which gives a speed ratio of 2.4 --172.71.114.70 14:48, 31 August 2023 (UTC)

You can pessimize time a tiny bit more by angling the path exactly 180° away from the bearing from Cueball to the guy in the ocean, assuming Cueball may only move in a straight line. 172.68.119.149 02:35, 1 September 2023 (UTC)

Is there a reference to the discredited but still believed by some "No eating before swimming" rule? By this measure "Here's an ice cream, go swimming" is monstrous in the same sense as "go play in traffic."162.158.158.106 15:45, 1 September 2023 (UTC)

I think the arrow for the last path may be interpreted as pointing up and away from Earth. This refers to the fact that in a curved spacetime if the universe has a spherical geometry it's possible to traverse the entire universe and come back to the starting point from below. This really maximizes time (and distance) while still moving in a straight line. --Unbroken (talk) 13:13, 10 January 2024 (UTC)