710: Collatz Conjecture
| Collatz Conjecture |
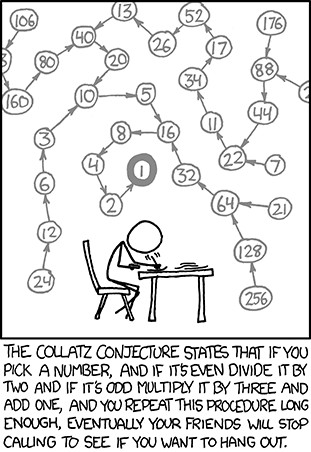 Title text: The Strong Collatz Conjecture states that this holds for any set of obsessively-hand-applied rules. |
Explanation[edit]
The Collatz conjecture is a longstanding unsolved problem in mathematics. It states that repeating the sequence of operations described in the comic will eventually lead to the number 1. The description in the comic starts out accurate, then veers into the joke. The comic illustrates the sequence with a graph in which an arrow connects each number to its successor. For example, the number 22 is even, so the next number in the sequence is 22 ÷ 2 = 11, and there is an arrow from 22 to 11. On the other hand, 11 is odd, so the next number is 3 × 11 + 1 = 34, and there is an arrow from 11 to 34. According to the caption, Cueball is obsessively writing out the graph by hand and is so preoccupied with the task that he has stopped socializing with his friends. He will be busy for a very long time, because the Collatz conjecture has been confirmed for all starting values up to 5 × 1018.
In the title text, the Strong Collatz Conjecture is a humorous extension of the Collatz Conjecture. Some other mathematical conjectures and axioms also have normal and Strong variants, where the Strong variant gives a more general rule. This practice is further parodied in 1310: Goldbach Conjectures.
Transcript[edit]
- [Cueball sits in a chair at a desk, papers piled on top, writing furiously. Depicted above are apparently the writing, a series of nodes in various Collatz sequences (starting with 7, 21, 24, 29, 106, 176 and 256), all eventually leading back to 1.]
- The Collatz Conjecture states that if you pick a number, and if it's even divide it by two and if it's odd multiply it by three and add one, and you repeat this procedure long enough, eventually your friends will stop calling to see if you want to hang out.
Trivia[edit]
This comic used to be available as a T-shirt in the xkcd store before it was shut down.
Discussion
Technically, the 1 should lead to the four, causeing a loop. Because (1*3)+1=4, 4/2=2, 2/2=1 xD -- 87.242.215.66 (talk) (please sign your comments with ~~~~)
- I'm pretty sure (follow the Wiki link, perhaps, although I haven't yet) there's an implicit "...eventually lead to one, then you can stop" for this process.
- And (again without checking the Wiki link), I suppose the conjecture could fail in one of two cases. Firstly if multiplying by three and adding one would take us to another odd number. Which cannot happen, because (odd*3) will be odd, so (odd*3)+1 is even. Which leads us to the possibility that the even number leads back to a prior odd number, to circle around again. There's no trivial case of (n*3)+1 => m, (m/2) => n, although there is the case of (n*3)+1 => m, (m/2) => o, (o/2) => n, for n=1. How, though, could we evaluate f1|2(xi) => xi+1 for all countably finite limits to i, given the rules of which f() function to use, to ensure that xi never equals x0. Now, that's a question and a half. Which I suspect has already been asked. And a half. 31.111.50.225 21:36, 7 May 2013 (UTC)
- Wonderful! "Without checking the wiki link"... The guy from 675: Revolutionary in real life!Mumiemonstret (talk) 15:14, 17 October 2014 (UTC)
- It's pretty obvious the person you replied to has a head for mathematics. If you really think this is at all similar to the Goatee Guy from 675: Revolutionary, then you are sorely mistaken. 172.68.59.84 13:40, 22 November 2018 (UTC)
- It seems way too general to be much more than "asked," and I am sure that it has been addressed in its simpler forms. In any case, there is enough amateur, recreational, and serious mathematical literature on it to find out that there are indeed two failure cases: a starting Collatz number results in an infinitely increasing sequence, or a loop exists apart from the 4-2-1 loop. (Curiously enough, some loops exist when negative numbers are allowed.) Stuff like this and Goldbach made me realize just how hard simple things can get. --Quicksilver (talk) 03:04, 20 August 2013 (UTC)
- A way to ask if the trajectory eventually reach 1 is to ask if the number is increasing or decreasing. If it is decreasing, it will eventually his a number already confirmed earlier to be on the trajectory. Whenever (n*3 + 1) is applied, the result is always even, and must be divided by two. But (n*3 + 1) / 2 > n. So the value will increase unless it hit a positive value more often than every other time. If it hit even 2 out of 3 times, the value decrease as (n*3 + 1) / (2*2) < n for all values of n > 1.
- The show can go on until it eventually hit a number m for which it is true that m = 2^x for some positive integer x. This value will take it all the way to the bottom. So the way the conjecture can be untrue is if some kind of loop exist, which either blow up the value towards infinity without ever hitting a 2^x number, or just forms a loop which bring it back to previous values. Again this can only be true if no 2^x number is ever reached. MigB (talk) 11:41, 13 April 2021 (UTC)
- Wonderful! "Without checking the wiki link"... The guy from 675: Revolutionary in real life!Mumiemonstret (talk) 15:14, 17 October 2014 (UTC)
Just for fun, here's 710's Collatz Trajectory.
0: 710
1: 355
2: 1066
3: 533
4: 1600
5: 800
6: 400
7: 200
8: 100
9: 50
10: 25
11: 76
12: 38
13: 19
14: 58
15: 29
16: 88
17: 44
18: 22
19: 11
20: 34
21: 17
22: 52
23: 26
24: 13
25: 40
26: 20
27: 10
28: 5
29: 16
30: 8
31: 4
32: 2
33: 1
International Space Station (talk) 09:36, 25 January 2016 (UTC)
I wrote a program to calculate the tree (Python 3.9), but you have to install treelib. Do this by typing 'pip install treelib' in the terminal. The program:
from treelib import *
tree=Tree()
levels=int(input('Levels of tree? '))
start=int(input('Starting number? '))
tree.create_node(start, start)
def f(x):
global tree
if tree.depth(x)==tree.depth():
return True
else:
return False
def collatz(x):
if x%2==0 and x%3==1 and x!=4:
return [(x-1)//3,x*2]
else:
return [x*2]
for i in range(levels):
N = list(tree.filter_nodes(f))
for i in N:
c=collatz(i.tag)
for j in c:
tree.create_node(j,j,i)
tree.show(line_type='ascii-ex')
--198.41.238.106 01:31, 28 July 2021 (UTC)
- If we're sharing code, I made a Python script that calculates a string for any given number and then graphs it:
import matplotlib.pyplot as plt
start_number = int(input("Enter a number:\n"))
loop_count = 0
full_list = [start_number]
while start_number != 1:
loop_count += 1
if start_number % 2 == 0:
start_number = int(start_number / 2)
print(start_number)
full_list.append(start_number)
elif start_number % 2 == 1:
start_number = int(start_number * 3 + 1)
print(start_number)
full_list.append(start_number)
else:
print("Error")
print("Iterations: " + str(loop_count))
plt.plot(full_list)
plt.title('Graph (Linear)')
plt.xlabel('Steps')
plt.ylabel('Hight')
plt.show()