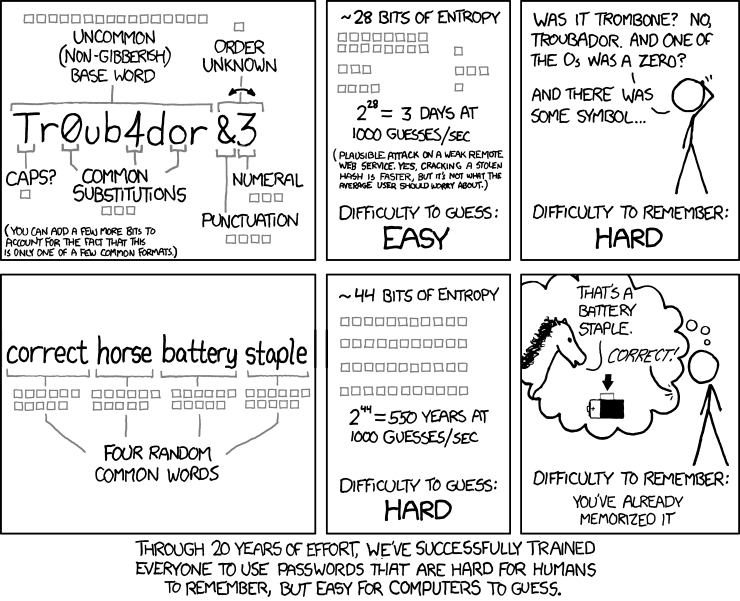
936: Password Strength
Explanation
This comic says that a password such as "Tr0ub4dor&3" is bad because it is easy for password cracking software and hard for humans to remember, leading to insecure practices like writing the password down on a post-it attached to the monitor. On the other hand, a password such as "correcthorsebatterystaple" is hard for computers to guess due to having more entropy but quite easy for humans to remember.
In simple cases the entropy of a password is calculated as a^b where a is the number of allowed symbols and b is its length. A dictionary word (however long) has a password space of around 65000, i.e. 16 bits. A truly random string of length 11 (not like "Tr0ub4dor&3", but more like "J4I/tyJ&Acy") has 94^11 = 72.1 bits. However the comic shows that "Tr0ub4dor&3" has only 28 bits of entropy. Another way of selecting a password is to have 2048 "symbols" (common words) and select only 4 of those symbols. 2048^4 = 44 bits, much better than 28. Using such symbols was again visited in one of the tips in 1820: Security Advice.
It is absolutely true that people make passwords hard to remember because they think they are "safer", and it is certainly true that length, all other things being equal, tends to make for very strong passwords and this can confirmed by using rumkin.com's password strength checker. Even if the individual characters are all limited to [a-z], the exponent implied in "we added another lowercase character, so multiply by 26 again" tends to dominate the results.
In addition to being easier to remember, long strings of lowercase characters are also easier to type on smartphones and soft keyboards.
xkcd's password generation scheme requires the user to have a list of 2048 common words (log2(2048) = 11). For any attack we must assume that the attacker knows our password generation algorithm, but not the exact password. In this case the attacker knows the 2048 words, and knows that we selected 4 words, but not which words. The number of combinations of 4 words from this list of words is (211)4 = 244, i.e. 44 bits. For comparison, the entropy offered by Diceware's 7776 word list is 13 bits per word. If the attacker doesn't know the algorithm used, and only knows that lowercase letters are selected, the "common words" password would take even longer to crack than depicted. 25 random lowercase characters would have 117 bits of entropy, vs 44 bits for the common words list.
- Example
Below there is a detailed example which shows how different rules of complexity work to generate a password with supposed 44 bits of entropy. The examples of expected passwords were generated in random.org.(*)
If n is the number of symbols and L is the length of the password, then L = 44 / log2(n).
| Symbols | Number of symbols | Minimum length | Examples of expected passwords | Example of an actual password | Actual bits of entropy | Comment | |
|---|---|---|---|---|---|---|---|
| a | 26 | 9.3 | mdniclapwz | jxtvesveiv | troubadorx | 16+4.7 = 20.7 | Extra letter to meet length requirement; log2(26) = 4.7 |
| a 9 | 36 | 8.5 | qih7cbrmd | ewpltiayq | tr0ub4d0r | 16+3=19 | 3 = common substitutions in the comic |
| troubador1 | 16+3.3=19.3 | log2(10) = 3.3 | |||||
| a A | 52 | 7.7 | jAwwBYne | NeTvgcrq | Troubador | 16+1=17 | 1 = caps? in the comic |
| a & | 58 | 7.5 | j.h?nv), | c/~/fg\: | troubador& | 16+4=20 | 4 = punctuation in the comic |
| a A 9 | 62 | 7.3 | cDe8CgAf | RONygLMi | Tr0ub4d0r | 16+1+3=20 | 1 = caps?; 3 = common substitutions |
| a 9 & | 68 | 7.2 | _@~"#^.2 | un$l|!f] | tr0ub4d0r& | 16+3+4=23 | 3 = common substitutions; 4 = punctuation |
| a A 9 & | 94 | 6.7 | Re-:aRo | ^$rV{3? | Tr0ub4d0r& | 16+1+3+4=24 | 1 = caps?; 3 = common substitutions; 4 = punctuation |
| common words | 2048 | 4 | reasonableretailsometimespossibly | constantyieldspecifypriority | reasonableretailsometimespossibly | 11×4=44 | Go to random.org and select 4 random integers between 1 and 2048; then go to your list of common words |
| correcthorsebatterystaple | 1 | Thanks to this comic, this is now one of the first passwords a hacker will try. The only entropy left is a boolean statement: "Is this password correcthorsebatterystaple, yes or no?" | |||||
- a = lowercase letters
- A = uppercase letters
- 9 = digits
- & = the 32 special characters in an American keyboard; Randall assumes only the 16 most common characters are used in practice (4 bits)
- (*) The use of random.org explains why
jAwwBYnehas two consecutive w's, whyRe-:aRohas two R's, why_@~"#^.2has no letters, whyewpltiayqhas no numbers, why "constant yield" is part of a password, etc. A human would have attempted at passwords that looked random.
People who don't understand information theory and security
The title text likely refers to the fact that this comic could cause people who understand information theory and agree with the message of the comic to get into an infuriating argument with people who do not — and disagree with the comic.
If you're confused, don't worry; you're in good company; even security "experts" don't understand the comic:
- Bruce Schneier thinks that dictionary attacks make this method "obsolete", despite the comic assuming perfect knowledge of the user's dictionary from the get-go. He advocates his own low-entropy "first letters of common plain English phrases" method instead: Schneier original article and rebuttals: 1 2 3 4 5 6
- Steve Gibson basically gets it, but calculates entropy incorrectly in order to promote his own method and upper-bound password-checking tool: Steve Gibson Security Now transcript and rebuttal
- Computer security consultant Mark Burnett almost understands the comic, but then advocates adding numerals and other crud to make passphrases less memorable, which completely defeats the point (that it is human-friendly) in the first place: Analyzing the XKCD Passphrase Comic
- Ken Grady incorrectly thinks that user-selected sentences like "I have really bright children" have the same entropy as randomly-selected words: Is Your Password Policy Stupid?
- Diogo Mónica is correct that a truly random 8-character string is still stronger than a truly random 4-word string (52.4 vs 44), but doesn't understand that the words have to be truly random, not user-selected phrases like "let me in facebook": Password Security: Why the horse battery staple is not correct
- Ken Munro confuses entropy with permutations and undermines his own argument that "correct horse battery staple" is weak due to dictionary attacks by giving an example "strong" password that still consists of English words. He also doesn't realize that using capital letters in predictable places (first letter of every word) does not increase password strength: CorrectHorseBatteryStaple isn’t a good password. Here’s why.
Sigh.
Transcript
- The comic illustrates the relative strength of passwords assuming basic knowledge of the system used to generate them.
- A set of boxes is used to indicate how many bits of entropy a section of the password provides.
- The comic is laid out with 6 panels arranged in a 3x2 grid.
- On each row, the first panel explains the breakdown of a password, the second panel shows how long it would take for a computer to guess, and the third panel provides an example scene showing someone trying to remember the password.
- [The password "Tr0ub4dor&3" is shown in the center of the panel. A line from each annotation indicates the word section the comment applies to.]
- Uncommon (non-gibberish) base word
- [Highlighting the base word - 16 bits of entropy.]
- Caps?
- [Highlighting the first letter - 1 bit of entropy.]
- Common Substitutions
- [Highlighting the letters 'a' (substituted by '4') and both 'o's (the first of which is substituted by '0') - 3 bits of entropy.]
- Punctuation
- [Highlighting the symbol appended to the word - 4 bits of entropy.]
- Numeral
- [Highlighting the number appended to the word - 3 bits of entropy.]
- Order unknown
- [Highlighting the appended characters - 1 bit of entropy.]
- (You can add a few more bits to account for the fact that this is only one of a few common formats.)
- ~28 bits of entropy
- 228 = 3 days at 1000 guesses/sec
- (Plausible attack on a weak remote web service. Yes, cracking a stolen hash is faster, but it's not what the average user should worry about.)
- Difficulty to guess: Easy
- [Cueball stands scratching his head trying to remember the password.]
- Cueball: Was it trombone? No, Troubador. And one of the O's was a zero?
- Cueball: And there was some symbol...
- Difficulty to remember: Hard
- [The passphrase "correct horse battery staple" is shown in the center of the panel.]
- Four random common words {Each word has 11 bits of entropy.}
- ~44 bits of entropy
- 244 = 550 years at 1000 guesses/sec
- Difficulty to guess: Hard
- [Cueball is thinking, in his thought bubble a horse is standing to one side talking to an off-screen observer. An arrow points to a staple attached to the side of a battery.]
- Horse: That's a battery staple.
- Observer: Correct!
- Difficulty to remember: You've already memorized it
- Through 20 years of effort, we've successfully trained everyone to use passwords that are hard for humans to remember, but easy for computers to guess.
External links
- Some info was used from the highest voted answer given to the question of "how accurate is this XKCD comic" at StackExchange [1].
- Similarly, a question of "how right this comic is" was made at AskMetaFilter [2] and Randall responded there.
- Also the Wikipedia article on 'Passphrase' is useful.
- In case you missed it in the explanation, GRC's Steve Gibson has a fantastic page [3] about this (and may have prompted this comic, as his podcast [4] about this was posted the month before this comic).
- This comic inspired How to memorize a random 60-bit string scientific paper (link is to the article about paper, wth paper itself linked)
- zxcvbn password strength estimator thanks this comic for the inspiration in acknowledgements.
- CMU paper: Correct horse battery staple: Exploring the usability of system-assigned passphrases
- Microsoft Password Guidance (page 8)
- The Guy Who Invented Those Annoying Password Rules Now Regrets Wasting Your Time, August 8, 2017 (this comic is reproduced in the article).
Discussion
Fix the software first. If you double the time it takes to enter each repeated password attempt you make brute force attacks pointless. Imagine you allowed a hurried user who screws up their own password entry w/ frozen fingers. If their system starts out with a 1 second delay, then doubles to two, then to four, etc. the time it takes to wait is 2^n. Six screw ups cost you a minute, twenty errors and you are waiting 291 hours before your next log-in attempt.... kmc 2015-05-10 108.162.229.124 (talk) (please sign your comments with ~~~~)
- That's not how brute force attacks work. They steal the hashes of the passwords and then brute force them locally. 198.41.235.107 23:43, 10 January 2016 (UTC)
- Both are brute force. It is specified in the comic that we assume an attack against a weak remote web service though. --162.158.150.231 13:10, 16 September 2016 (UTC)
You still have to vary the words with a bit of capitalization, punctuation and numbers a bit, or hackers can just run a dictionary attack against your string of four words. Davidy²²[talk] 09:12, 9 March 2013 (UTC)
- Several discussions around the internet around this -- the consensus [ http://www.explainxkcd.com/wiki/index.php/936 looks like] that once this scheme is published it is fairly simple to run a dictionary attack on the password. My advise to most people is to use a password manager like lastpass or onepass that can generate pure random password. 162.158.253.6 23:52, 10 March 2016 (UTC)
No you don't. Hackers cannot run a dictionary attack against a string of four randomly picked words. Look at the number of bits displayed in the image: 11 bits for each word. That means he's assuming a dictionary of 2048 words, from which each word is picked randomly. The assumption is that the cracker knows your password scheme. 86.81.151.19 20:17, 28 April 2013 (UTC) Willem
- I just wrote a program to bruteforce this password creation method. https://github.com/KrasnayaSecurity/xkcd936/blob/master/listGen936.py Once I get it I'll try coming up with more bruteforcing algorithms such as substituting symbols, numbers, camel case, and the like. Point is, don't rely on this or any one method. I wouldn't be surprised if the crackers are already working on something like this. Lieutenant S. (talk) 07:03, 8 September 2014 (UTC)
- It took 1.25 hours to bruteforce "correcthorsebatterystaple" using the 2,000 most common words with one CPU. Lieutenant S. (talk) 07:09, 9 September 2014 (UTC)
- 1) ... as compared to 69 milliseconds for the other method. 2) Since you are able to test 3,9 billion passwords as second (very impressive!) I am guessing that your setup is not performing its attack over a ”weak remote service”, which is breaking the rules of the #936 game. 3) five words and a 20k-wordlist would get you 9400 years (still breaking the weak remote service rule).--Gnirre (talk) 09:13, 14 October 2014 (UTC)
- 2) Two thoughts: You use itertools.permutations, which only covers non-repeating words, but mainly you don't actually hash the password. If you have a plain-text password, there no need to crack the password because you could just look at it. Example of an actual crack for this type of password: https://github.com/koshippy/xkcd_password/blob/master/password_crack.py My computer gets 10,000,000 guesses in ~16 seconds (non-hashed takes ~2 seconds), meaning it would take almost a year to try every combination. (2048^4 total password space). Even optimizing by using c++/java or JtR, you wouldn't see huge improvement since most of the time is from the SHA hashing. Point being: a typical user can't crack this type of password in a short amount of time, even if they know your wordlist. 199.27.128.212 12:05, 17 February 2015 (UTC) Koshippy
Sometimes this is not possible. (I'm looking at you, local banks with 8-12 character passwords and PayPal) If I can, I use a full sentence. A compound sentence for the important stuff. This adds the capitalization, punctuation and possibly the use of numbers while it's even easier to remember then Randall's scheme. I think it might help against the keyloggers too, if your browser/application autofills the username filed, because you password doesn't stand out from the feed with being gibberish. 195.56.58.169 09:01, 30 August 2013 (UTC)
The basic concept can be adapted to limited-length passwords easily enough: memorize a phrase and use the first letter of each word. It'll require about a dozen words (you're only getting 4.7 bits per letter at best, actually less because first letters of words are not truly random, though they are weakly if at all correlated with their neighbors -- based on the frequencies of first letters of words in English, and assuming no correlation between each first letter and the next, I calculate about 4 bits per character of Shannon entropy). SteveMB 18:35, 30 August 2013 (UTC)
Followup: The results of extracting the first letters of words in sample texts (the Project Gutenberg texts of The Adventures of Huckleberry Finn, The War of the Worlds, and Little Fuzzy) and applying a Shannon entropy calculation were 4.07 bits per letter (i.e. first letter in word) and 8.08 bits per digraph (i.e. first letters in two consecutive words). These results suggest that first-letter-of-phrase passwords have approximately 4 bits per letter of entropy. --SteveMB (talk) 14:21, 4 September 2013 (UTC)
Addendum: The above test was case-insensitive (all letters converted to lowercase before feeding them to the [frequency counter]). Thus, true-random use of uppercase and lowercase would have 5 bits per letter of entropy, and any variation in case (e.g. preserving the case of the original first letter) would fall between 4 and 5 bits per letter. --SteveMB (talk) 14:28, 4 September 2013 (UTC)
I just have RANDOM.ORG print me ten pages of 8-character passwords and tape it to the wall, then highlight some of them and use others (say two down and to the right or similar) for my passwords, maybe a given line a line a little jumbled for more security. 70.24.167.3 13:27, 30 September 2013 (UTC)
- Remind me to visit your office and secretly replace your wall-lists by a list of very similar looking strings ;) --Chtz (talk) 13:53, 30 September 2013 (UTC)
Simple.com (online banking site) had the following on it’s registration page:
“Passphrase? Yes. Passphrases are easier to remember and more secure than traditional passwords. For example, try a group of words with spaces in between, or a sentence you know you'll remember. "correct horse battery staple" is a better passphrase than r0b0tz26.”
Online security for a banking site has been informed by an online comic. Astounding. 173.245.54.78 21:22, 11 November 2013 (UTC)
The Web service Dropbox has an Easter egg related to this comic on their sign-up page. That page has a password strength indicator (powered by JavaScript) which changes as you type your password. This indicator also shows hints when hovering the mouse cursor over it. Entering "Tr0ub4dor&3" or "Tr0ub4dour&3" as the password causes the password strength indicator to fall to zero, with the hint saying, "Guess again." Entering "correcthorsebatterystaple" as the password also causes the strength indicator to fall to zero, but the hint says, "Whoa there, don't take advice from a webcomic too literally ;)." 108.162.218.95 15:17, 11 February 2014 (UTC)
The explanation said that the comic uses a dictionary[5]. In fact it's a word list, which seems similar but it's not. All the words in the word list must be easy to memorize. This means it's better not to have words such as than or if. Also, it's better not to have homophones (wood and would, for example). The sentence dictionary attack doesn't apply here. A dictionary attack requires the attacker to use all the words in the dictionary (e.g. 100,000 words). Here we must generate the 17,592,186,044,416 combinations of 4 common words. Those combinations can't be found in any dictionary. At 25 bytes per "word" that dictionary would need 400 binary terabytes to be stored. Xhfz (talk) 21:37, 11 March 2014 (UTC)
This comic was mentioned in a TED talk by Lorrie Faith Cranor on in March 2014. After performing a lot of studies and analysis, she concludes that "pass phrase" passwords are no easier to remember than complex passwords and that the increased length of the password increases the number of errors when typing it. There is a lot of other useful information from her studies that can be gleaned from the talk. Link. What she doesn't mention is the frequency of changing passwords - in most organizations it's ~90 days. I don't know where that standard originated, but (as a sys admin) I suspect it's about as ineffective as most of our other password trickery - that is that it does nothing. Today's password thieves don't bash stolen password hash tables, they bundle keyloggers with game trainers and browser plugins.--173.245.50.75 18:14, 2 July 2014 (UTC)
- Lorrie Faith Cranor gets the random part of #936 word generation correct, which is great. Regarding memorizability, this study (https://cups.cs.cmu.edu/soups/2012/proceedings/a7_Shay.pdf) does not address #936. The study uses no generator for gibberish of length 11. Most comparable are perhaps two classes of five or six randomly assigned characters. None of the study's generators has 44 bits of entropy – its dictionary for the method closest to #936 – noun-instr – contains only 181 nouns. The article contains no discussion of the significance of these differences to #936. In her TED Lorrie Faith Cranor says ”sorry all you xkcd fans” which could be interpreted as judgement of #936, but there is no basis in the above article for that. It does however seem plausible that the report could be reworked to address #936. --Gnirre (talk) 10:42, 14 October 2014 (UTC)
- Password-changing frequency isn't about making passwords more secure, but instead it's about mitigating the damage of a successfully cracked password. If a hacker gets your password (through any means) and your password changes every 90 days, the password the hacker has obtained is only useful for a few months at most. That might be enough, but it might not. If the hacker is brute forcing the passwords to get them, that cuts into the time the password is useful. --173.245.54.168 22:22, 13 October 2014 (UTC)
- However, brute-forcing gets much easier that way.
- Say the average employee is around for 10 years, which is reasonable for some companies , absurdly high for others, and a bit low for a family business. That's 40 password changes.
- Now if you have to remember another password every now and then, you sacrifice complexity, lest you forget it. A factor of 40 is like one character less. But how much shorter will the password be? It's more likely that it's gonna be 3 or 4 characters less. Congrats, you just a factor of 1000's for a perceived "mitigation", which doesn't even work. Pro attackers can vacuum your server in a DAY once they have the PW. 141.101.104.53 13:03, 4 December 2014 (UTC)
Just because you are required to have a password that has letters and numbers in it doesn't mean you can't make it memorable. When caps are required, use CamelCase. When punctuation is required, make it an ampersand (&) or include a contraction. When numbers are required, pick something that has significance to you (your birthday, the resolution of your television, ect.). Keep in mind that, if your phrase is an actual sentence, the password entropy is 1.1 bits per character (http://what-if.xkcd.com/34), so length is key if you want your password to be secure. (Though no known algorithm can actually exploit the 1.1 bits of entropy to gain time, so it might be more like 11 bits of entropy per word. Even then, my passwords have nonexistent and uncommon words in them, (like doge or trope), which also adds some entropy.) 108.162.246.213 22:18, 1 September 2014 (UTC)
- Flip side of the story, the "capital plus small plus other char" policy doesn't make your password any safer.
- The German company T-online had an experimental gateway with the password, "internet". Now that sucked. No problem, tho, because that gateway wasn't accessible from outside. When they went live, they "improved" the password to "Internet1". There are still lots of these passwords around: first letter is a Cap, and the only non-alphabetic char is a 1 at the end. This doesn't add any entropy. 141.101.104.53 13:03, 4 December 2014 (UTC)
- This shows that about one third of all digits in a sample of passwords was "1" . 141.101.104.53 13:14, 4 December 2014 (UTC)
You can also troll the brute-force engine by using words from other languages, fictional books and video games.--Horsebattery (talk) 03:04, 3 November 2014 (UTC)
- That's a good idea; it adds to the entropy bits per word. If you really want to throw them off, mix different languages. Just don't use very well-known words; I'm sure the hackers have cojones and Blitzkrieg in their dictionaries. 141.101.104.53 13:03, 4 December 2014 (UTC)
Also, passwords that are 'hard to remember' are themselves a security vulnerability. A password reset scheme (or even a lockout scheme) is a vulnerability. The more it needs to be used, the harder it becomes to police that vulnerability. Relatedly, hard-to-remember passwords leave users uncertain whether their password has been changed by someone else or they've just forgotten it. Ijkcomputer (talk) 15:32, 18 December 2014 (UTC)
Hi there, this comic gave me the idea for a password generator that can (optionally) use dictionary words. Have a look if you're interested: https://wordypasswords.com Use your common sense though about what is and isn't secure! Hope someone finds it useful. Mackatronic (talk) 08:23, 9 January 2015 (UTC)
I have not read all of the replies and in truth most of the detail is boring to me but it has occurred to me that with this sort of problem and since the Snowden affair, serious security devices will have to make the keyboard redundant.
At the moment all I can imagine is a series of pictures like hieroglyphs but even using a rolling code of ever changing font glyphs would do. When the security required by money minders reaches the stage of development possible with keyboards that can supply that sort of security, we will have some idea which banks have some idea about security.
Tip: Not Barings. They have an history of intransigence and stupidity. (Still revered in banks though as able to cure colon cancer with poor investment strategies.)
I used Google News BEFORE it was clickbait (talk) 13:46, 23 January 2015 (UTC)
The D0g..................... (24 characters long) is NOT stronger than PrXyc.N(n4k77#L!eVdAfp9 (23 characters long). The reason why, is that the later password is random. There is no pattern. The former, "padding" technique can be very easily cracked. You just need to assume that each character be repeated 1~30 times. Then the first password would become : 1(D)1(0)1(g)21(.), which, is then of complexity 30^4 + 96^4, versus 96^23 for the random password. And that is assuming that any character can be repeated 1~30 times, so DDDDDDDDD0000000ggggggg...... also would be cracked extremely quickly. If you limit yourself to only last character padding, your password now becomes 30*96^4 possibilities. 108.162.222.235 (talk) (please sign your comments with ~~~~)
And that's why it is stupid to explain this kind of joke : it depends on many (MANY) parameters such as brute-force method and encryption/hash algorithm. Giving this kind of (wrong) explanations about "pass cracking" (as if it was always the same way to process ...) is ridiculous. And they talk about entropy .......... Holy shit, go back to school and stop screwing cryptography up. zM_
I just use a password with a ␡ character or two, and ␇ for banks. 108.162.242.21 08:33, 18 August 2015 (UTC)
I'am astonished that even someone like Schneier don't get 936 right immediately after reading it. So, I think I know what was going on in Munroes mind conceptually. Maybe there are some grans of salt, but I don't have a problem with these. But I do have one (or two) quantitative problem(s) with 936:
- I was not able to find out, how Munroe get the value of about 16 bits of entropy for the "uncommon" nine letter lower case "non-gibberish base word". This would mean: On average, a letter of such a word will have about 1.8 bits of entropy. May be, but how do we know? "Citation needed!" ;-)
- (Secondly: The "punctuation" should have 5, not 4 bits of entropy. There are 32 (2^5) ASCII punctuation characters (POSIX class [:punct:]). But I assume this is a lapse.)
Can someone enlighten me? --162.158.91.236 17:31, 19 September 2015 (UTC)
- I have missed the sentence "Randall assumes only the 16 most common characters are used in practice (4 bits)". Hm. There is a huge list with real world passwords out there, leaking from RockYou in 2009. After some processing to remove passwords containing characters that are not printable ASCII characters (ñ, £, ๅ, NBSP, EOT, ...), the list contains about 14329849 unique passwords from about 32585010 accounts (there are some garbage "passwords" like HTML code fragments). The following are the number of accounts using a password containing a particular printable character (one or more tokens of a particular type):
226673 .
186883 _
179264 !
125846 -
104224 @
95237 *
92802 (space)
60002 #
36522 /
31172 $
28550 &
27686 ,
23905 +
18704 =
18268 )
17927 ?
16401 (
16074 '
14407 ;
11819 <
11118 %
10723 ]
8975 \
7718 [
7209 :
5815 ~
5673 ^
4995 `
2847 "
2741 >
1050 {
939 }
502 |
(NB: 1222815 accounts were using a password containing at least one of these.)
- Sorry, I have no "citation". But you can play with the leaked RockYou password list yourself. Here is a way to reach that playground:
$ # Download the compressed list (57 MiB; I have no idea what "skullsecurity"
$ # is, it was simply the first find and I assume it's the said list):
$ wget http://downloads.skullsecurity.org/passwords/rockyou-withcount.txt.bz2
$ # Decompress the list (243 MiB), or, to speak more exact, it's a table:
$ bzip2 -dk rockyou-withcount.txt.bz2
$ # The content of the table is: "How many accounts (first row) were using that
$ # password (second row)?" Let's take a peek:
$ head -n5 rockyou-withcount.txt
290729 123456
79076 12345
76789 123456789
59462 password
49952 iloveyou
$ # The following command processes the table to remove lines with passwords
$ # containing characters that are not printable ASCII characters (14541
$ # lines/passwords, 18038 accounts), and lines insisting that there were some
$ # accounts with no password (1 line, 340 accounts). Moreover, the command
$ # removes every space character not belonging to a password, makes the rows
$ # tab-delimited and writes the result in a file called "ry" (161 MiB; many
$ # bloating spaces removed).
$ LC_ALL=C sed -n 's/^ *\([1-9][0-9]*\) \([[:print:]]\{1,\}\)$/\1\t\2/p' rockyou-withcount.txt >ry
$ # The following are shell functions to build commands. They will be explained
$ # below using examples (I can not express myself well in this language).
$ counta() { LC_ALL=C awk 'BEGIN { FS = "\t"; p = 0; a = 0 } { if ($2 ~ /'"$(printf %s "$1" | sed 'sI/I\\/Ig')"'/) { p++; a += $1 } } END { print a " (" p ")" }' "$2" ;}
$ countap() { LC_ALL=C awk 'BEGIN { FS = "\t"; p = 0; a = 0 } { if ($2 ~ /'"$(printf %s "$1" | sed 'sI/I\\/Ig')"'/) { p++; a += $1; print $0 } } END { print a " (" p ")" }' "$2" ;}
$ # We have reached the playground. Here are some examples for how to use the
$ # toys:
$ # Count how many accounts were using a password containing the string love:
$ counta 'love' ry
671599 (188855)
$ # The first operand of the above command is a extended regular expression
$ # (ERE). The second operand is a file, namely the previously generated file
$ # called "ry", that is the (processed) table. The first number of the output
$ # means: "That many accounts were using a password matching the ERE." The
$ # second number inside parentheses means: "That many unique passwords matching
$ # the ERE." If the first number is greater than the second number, some
$ # accounts sharing the same password (we will see this clearly in one of the
$ # examples below).
$ # Count how many accounts were using a password containing at least one
$ # character:
$ counta '.' ry
32585010 (14329849)
$ # Count how many accounts were using a password containing exactly one
$ # character:
$ counta '^.$' ry
144 (45)
$ # Count how many accounts were using a password containing exactly one numeric
$ # character:
$ counta '^[0-9]$' ry
55 (10)
$ # Let's have a look at the distribution:
$ countap '^[0-9]$' ry
29 1
6 7
6 3
3 9
3 2
2 6
2 5
2 0
1 8
1 4
55 (10)
$ # Obove we see the second command at work. You see what it does and what it
$ # does different. And here we see clearly the meaning of the first number and
$ # the second number inside parentheses.
$ # Count how many accounts were using a password containing at least one
$ # numeric character:
$ counta '[0-9]' ry
17609065 (9761364)
$ # Count how many accounts were using a password ending with a numeric
$ # character:
$ counta '[0-9]$' ry
15728238 (8313698)
$ # Count how many accounts were using a password beginning with a numeric
$ # character:
$ counta '^[0-9]' ry
6409397 (3283946)
$ # Count how many accounts were using a password containing only numeric
$ # characters:
$ counta '^[0-9]+$' ry
5192990 (2346744)
$ # And, last but not least, count how many accounts were using a password
$ # containing that "uncommon non-gibberish base word" in 936, with an upper
$ # or an lower case first letter, with or without some of the "common
$ # substitutions":
$ counta '[tT]r[o0]ub[a4]d[o0]r' ry
3 (3)
$ # Yes, there are some. 14 million unique passwords are a lot. Let's see what
$ # exactly was used:
$ countap '[tT]r[o0]ub[a4]d[o0]r' ry
1 troubador1
1 troubador
1 darktroubador
3 (3)
- 162.158.91.236 06:23, 21 September 2015 (UTC)
Interesting read about the generated password streangth: https://www.schneier.com/blog/archives/2016/01/friday_squid_bl_508.html#c6714590 162.158.91.190 08:09, 8 January 2016 (UTC)
- That person sounds confused. 198.41.235.107 23:43, 10 January 2016 (UTC)
- You've Already Memorized It
Originally I logged in to report a local xkcd related phenomenon, and ask if anyone else had experienced it. The destiny, seemingly inescapable, that at once became my own upon seeing that last panel; the effect of the self-fullfilling combination of the very specific look of inquiry -- one I recognize immediately and associate with the words "interesting, Captain" -- and the insidiously performative "You've already memorized it." At first I doubted this was actually the case, but soon I could no longer, since not only did the phrase readily come to the mind and out the mouth, it also came up often. The "correct" soon replaced the word "right" in everyday conversation, then "right you are" and "yes" and so forth, then its opposite (with a "no" in front), then replacing the direction, the verb involving pen and paper (the most recent development was merely a quick under the breath aside of an acronym of the remaining words). All followed by the rest of the absurdly perfect password. Now here's the kicker: I logged on to tell you all this for some reason, only to find, I had memorized "correct horse staple battery" instead of "correct horse battery staple."A female faust (talk) 03:58, 31 July 2016 (UTC)
- If you go to https://howsecureismypassword.net/ and type in the suggested password in the comic, it says that the password would be cracked instantly, and adds a section titled "xkcd".
162.158.62.195 14:18, 11 February 2017 (UTC)
Would you believe it, the guy who made the bad password rules switched his philosophy to this comic's: "Long, easy-to-remember phrases now get the nod over crazy characters" "In a widely circulated piece, cartoonist Randall Munroe calculated it would take 550 years to crack the password “correct horse battery staple,” all written as one word. The password Tr0ub4dor&3—a typical example of a password using Mr. Burr’s old rules—could be cracked in three days" That's right, Jacky720 just signed this (talk | contribs) 11:57, 8 August 2017 (UTC)
The 44 bits of entropy breaks down rapidly when you realize in real life, most people will choose a passphrase that contains words like "pass", "phrase", "remember", "long", "company" and quite likely "stupid". It's the passphrase equivalent of "password123". If the words are selected randomly and then assigned to a person, that would fix that problem (but create others, like mistrust of a computer that assigns passwords for you to log into that same computer with). Nerfer (talk) 21:19, 11 October 2019 (UTC)
There is one aspect which has been left out the whole time. I do not question things like wordlist length, entropy, or substitutions. However, doing shoulder surfing will either reveal a full password or in parts. A full password should not be topic of discussion. In the case of partial success, it is in the proposed method far easier to guess the rest of the password than in the traditional one. CommingFromTheSide (talk) 15:16, 5 November 2019 (UTC)
As for "author's 28 bits mistake". I believe that Randall does mean the common lexicon with mangling substitutions. That means that counterexample "J4I/tyJ&Acy" does have 72bits, but nonetheless is irrelevant to character/personage strategy of choosing a memorable yet strong password. 172.68.215.113 13:17, 23 February 2020 (UTC)
Ah... this reminds me of one of my old password.
> It had quote.
> It had comments.
> There were "10e9 characters". (Don't worry, as much as it length backfired, if you types fast, you could type by hand in less than 5 minutes)
> It had typo.
> It had hints of itself in itself.
--172.68.154.70 08:22, 8 April 2020 (UTC)
Ah yes, now Microsoft has disabled plaintext words in passwords. I can see where they were trying to go with this but it completely backfired for everyone who doesn't use the password "password". -Alpha2 (talk) 15:20, 13 October 2021 (UTC)
This scheme (four words) was used for the default wifi and admin passwords on a T Mobile wireless home internet gateway received on 2022-Jun-23 --172.70.175.146 14:51, 27 June 2022 (UTC)
The best password/passphrase should be something that has meaning to you and only you; for example, I used to use the password NurseSlutButt, which came from working at an office where the manager had one of his walls covered with the employees' personal memorabilia and one of those was a 1959 newspaper clipping about the new matron of a local orphanage, so that phrase developed from idly staring at the clipping and thinking about her and how she looked in the accompanying photo. I never told anyone about that password until now. Also, introduce deliberate mis-spellings: that makes it harder to crack, even if the attacker guesses the word. That was probably the intent behind the "numbers & symbols" rule in the first place, back before Unicode existed and computer users were limited to what was on their keyboard. 172.71.215.11 23:37, 17 November 2023 (UTC)