45: Schrodinger
| Schrodinger |
| Title on LiveJournal: Drawing: Schrodinger |
 Title text: There was no alt-text until you moused over |
This was the forty-second comic originally posted to LiveJournal. The previous one was 39: Bowl, and the next one was 46: Secrets. It was among the last eleven comics posted both on LiveJournal and on xkcd.com after the new site was launched. This comic was published on the same day across both sites, but not all of them shared the same posting day.
Explanation[edit]
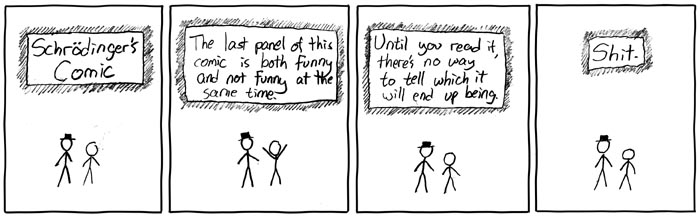
This comic is a joke creating a humorously false synthesis, combining the principles of quantum superposition and the effects of reading a comic one panel at a time. Schrödinger's cat is a thought experiment that illuminates the notion that a particle only resolves itself to its state upon observation, and until such observation is made, it is in all of its possible states simultaneously. In the thought experiment, a cat is both dead and alive until observation; likewise, in this comic, Black Hat and Cueball are likening the last panel to the box with the cat: until you read it, it is in a mixed state (a superposition) of both funny and unfunny. Finally, in the last panel, both of them say "Shit." The joke is that after reading the last panel, the comic is both funny (as it is unexpected) and not funny (as the last line was a non sequitur and therefore there is no climax) at the same time, thus proving Black Hat and Cueball wrong, hence them expressing discontent with the word "shit."
The title text, which Randall here unusually calls "alt-text", implies that it might only come into existence when the mouse over action takes place. This is another reference to the Schrödinger's cat concept, where the user can't determine if the title text exists until they hover the mouse over it. So, prior to hovering, the title text might be absent or present.
Schrödinger's cat[edit]
Schrödinger's cat is a famous thought experiment proposed by Erwin Schrödinger to question the Copenhagen interpretation of quantum mechanics. Under the Copenhagen interpretation, any particle is described by a wave function that allows one to calculate the probability that it is any given state. A radioactive nucleus with a half-life of one hour, for instance, would have a wave-function that would split, showing two distinct states (decayed, undecayed) that change over time until some "observation" forced the wave-function into one state or another (called "collapsing the wave-function"). Before the wave-function is collapsed, it is incorrect to say that the atom has decayed or has not decayed; it is in a "superposition" of states, effectively both decayed and undecayed.
Schrödinger thought that the Copenhagen interpretation was absurd and devised a thought experiment to demonstrate it. The experiment consisted in putting a cat in a box with a device triggered by the decay of an atom with a half-life of one hour that would release a poisonous gas if triggered. Then, after waiting an hour, the Copenhagen interpretation would say that the atom is in a superposition of decayed and undecayed states, and thus, by extension, the cat would be in a superposition of alive and dead states. Only when the box is opened would the wave-function for the cat collapse into either alive or dead states. This thought experiment is not meant to be taken literally, as every interaction of a particle with another constitutes an observation, and many particles must interact for a cat to die, but still his argument was that since it is absurd for a cat to be both alive and dead, it is absurd for an atom to be both decayed and undecayed. If this experiment were to be performed, the cat would not be both dead and alive.
Transcript[edit]
- [Black Hat and Cueball are standing next to each other. Above them the text is written in a box with shades around it.]
- Schrödinger's Comic
- [Black Hat and Cueball are still standing next to each other, but Cueball has lifted his arms above his head. The text is again written in a box with shades around it.]
- The last panel of this comic is both funny and not funny at the same time.
- [Black Hat and Cueball are still standing next to each other, Cueball arms are down again. The text is again written in a box with shades around it.]
- Until you read it, there's no way to tell which it will end up being.
- [Black Hat and Cueball are still standing next to each other. Cueball has become smaller and smaller through the three frames after the first. Quite clearly here in the last panel. The text is again written in a box with shades around it.]
- Shit.
Trivia[edit]
- There had been a break of almost a month between this and the previous comic. This time was probably used to prepare the launch of the xkcd.com. See LiveJournal.
- This was the first comic to be posted on the same day on both LiveJournal and xkcd.com.
Discussion
There were no comments until you scrolled down. 108.162.219.246 20:21, 1 December 2014 (UTC)
- There were two comments before you scrolled down. 173.245.56.130 12:02, 17 October 2015 (UTC)
...shit...--TheTimeBandit (talk) 21:20, 30 October 2017 (UTC)
I read it as: The comic is not funny, and thus the curse word is because it's not funny. Does anyone else agree? 162.158.63.172 (talk) 01:22, 5 February 2021 (UTC) (please sign your comments with ~~~~)
This is the BEST for me, so my cat ended up being funny 162.158.129.112 15:12, 22 May 2023 (UTC)
I find this funny every time. Is this bad? Have I disproved Schrödinger? Psychoticpotato (talk) 19:58, 20 May 2024 (UTC)
- No you just happen to be from a universe where the comic is actually funny. But if we debate about the funniness of the comic then the interference pattern in these comments will collapse and we'll be forced into the funny or unfunny version of the comic. IAmADroid (talk) 03:33, 15 August 2024 (UTC)
 Add comment
Add comment
