687: Dimensional Analysis
| Dimensional Analysis |
 Title text: Or the pressure at the Earth's core will rise slightly. |
Explanation[edit]
Cueball has a hobby: showing correct calculations according to the dimensional analysis, but with ridiculous correlations of uncorrelated events and measurements. Here Cueball is giving a talk and uses this trick to convince his listeners that the Toyota Prius combined EPA gas mileage is somehow connected to the constant π via the Planck energy, the pressure at the Earth's core and the width of the English Channel.
Scientists — often physicists — use dimensional analysis to quickly check if a given formula can possibly relate to a physical system, because if you end up with an equation claiming that Joules are meters, something is clearly wrong. Dimensional analysis here refers to the check if both sides of the equation arrive at the same physical unit when the units of all variables get plugged into the equation. This requires knowledge of the system of units and the relation between different physical units. Cueball uses the following equation to make a mockery of the practice:
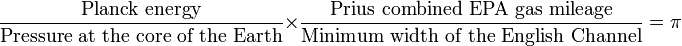
Dimensional analysis[edit]
The right hand side is dimensionless, it's the constant π = 3.14... which is defined by the relation of two lengths, the circumference and the diameter of a circle. The left hand side requires to plug in the dimensions of the named physical quantities:
- Planck energy: given in Joules [J]
- Pressure at the core of the Earth: often given in Pascals [Pa]
- In this case, the relationship is used of 1 Pascal [Pa] = 1 Joule per cubic meter [J/m³]
- Prius combined EPA gas mileage: miles per gallon, given in meters per cubic meter [m/m³]
- Fuel efficiency has two formats that are commonly used: length per volume and volume per length. The former must be used here in order to get the units to cancel correctly.
- Minimum width of the English Channel: given in meters [m]
When plugged into the left-hand side, this amounts to:
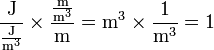
Note that for dimensional analysis constant factors are not taken into account. Here square brackets are used to denote dimensional analysis. In the above equation the unit of energy (joule) as well as all the unit of volume (cubic meter) cancel out each other.
Another aspect of the comic is that sometimes dimension analysis of equations that were not derived but rather "made up" can provide insight. For instance the inverse of gas mileage, fuel consumption per distance, is dimensionally a surface. If a car consumes 10 liters per 100 km, i.e. 10 dm3 / 100 km, this value has a dimension of m3 / m = m2. This surface corresponds to the area of an imagined cylinder (or other prism) of fuel along the road that the car consumes as it rides along, 0.1 mm2 in the example. However, in reality such an equation would have to be somehow "motivated", which is more of an art than science and requires great experience in the field the equation should relate to. The presented equation combines values that have no immediate causal relation with each other, so it does not make sense. Furthermore, since the values have absolutely no causal relation to each other, the ratios presented are simple coincidence; despite Cueball's claim, building a better Prius would not cause any changes to the English Channel.[citation needed]
The title text also refers to this, as a higher pressure at Earth's core could also balance the equation, keeping the result constant equal to π. The Planck energy is an absolute, however, so it is not mentioned as a way to balance the next version of Prius.
Some numbers for this calculation[edit]
The Planck energy is the only nearly exact value we do have. Compared to other Planck values it is very large (macroscopic).
E_planck = 1.956 x 109 J
Pressure at the core of the Earth ranges from 330 to 360 gigapascals. Using a simple value like this:
P_core = 350 GPa = 3.5 x 1011 J/m³
Prius combined EPA gas mileage: For the third generation (from 2010) the combined EPA gas mileage is 50 miles per gallon.
50 mpg => 21,000,000 m/m³
Minimum width of the English Channel is about
33.1 km = 33,100 m
Calculating from these values you will get π = 3.54... that is pretty close to π = 3.14... while using a Planck value. According to Cueball this will be within the experimental error (the combined error for all four numbers - none are exact numbers). For instance if you tried the ePrius you would may get closer to pi — as the distance per fuel quantity in real life usage usually is somewhat lower than the standardized test value advertised — and that would reduce the result.
Wolfram|Alpha can find most of the statistics and do the calculations.
Transcript[edit]
- My Hobby:
- Abusing dimensional analysis
- [On a blackboard.]
- (Planck energy/Pressure at the Earth's core) x (Prius combined EPA gas mileage/Minimum width of the English Channel) = π
- [Cueball indicates this equation with a pointer in front of a class.]
- Cueball: It's correct to within experimental error, and the units check out. It must be a fundamental law.
- Student: But what if they build a better Prius?
- Cueball: Then England will drift out to sea.
Trivia[edit]
After this comic was released, Toyota released a better Prius. As of the 2025 model year achieving 57 mpg, England must have drifted out to sea by ~4.5km, making the English Channel about 37.7 kilometers wide.
Discussion
Is it customary to just slap a new contributor after 5 minutes because the page was not done perfectly on the first editing? Now I will NOT research and add the actual numbers you would have to plug into the equation and I will leave this to Dave22. Genius. Stamfest (talk) 09:36, 1 April 2013 (UTC)
- We do put those fields there for a reason. Most editors just make a page and leave them incomplete with fields deleted or blank, oftentimes leaving admins with heaps of maintenance work to deal with. I probably *should* have waited for you to finish, but prior experience and me being busy with two simultaneous continuously updating comics led me to treat it like most other incomplete pages. Will wait in the future though, since I know how you edit now. Discussion hidden, as it covers matters outside of the comic. Davidy²²[talk] 10:01, 1 April 2013 (UTC)
- And I added the comment of a (very) initial explanation to the initial version. If you only want immediately perfect content, then just say so at page creation-time. This is totally against all wiki rules I have ever experienced. It is also against basic netiquette to call new contributors names upon their first submission. You might consider to change your attitude if you run or are involved with such a project. OTOH, if this is YOUR project, you are free to treat contributors all the way you want, but do not expect them to add more content if you behave like that. But the good thing is: your reaction shifted my attention back to work. Thanks for that. This won't help the page, though. Bad luck, I guess. Also, I only found out now that it is not possible to delete accounts on a wikimedia wiki... Stamfest (talk) 13:10, 1 April 2013 (UTC)
- Someone posted that I've been wasting electrons on here. I didn't quite know how to take that, it being true and all. I had the impression that it was the whole point of comics that you waste time on them. Some of us just have too many electrons; obviously. I used Google News BEFORE it was clickbait (talk) 16:33, 27 January 2015 (UTC)
- Then they should stop being so negative and get some grounding. Promethean (talk) 13:26, 27 February 2018 (UTC)
This comments should be removed from this topic. --Dgbrt (talk) 20:22, 14 May 2013 (UTC)
I am not sure if this is relevant but I laughed more reading Stamfest vs Daviddy22 then Randall :D but Dgbrt may have a point of removing it. 173.245.62.83ck
Made a minor addition to the explanation as it relates to the "Buckingham Pi" formalization. This may be a 2nd order pun in the comic.Tardyon (talk) 15:05, 3 February 2014 (UTC)
The units only check out if mileage is given in the form liters/100 km. If you use miles/gallon you end up with units of length^-4.108.162.217.5 22:17, 13 November 2014 (UTC)
Or, maybe the Plank Energy will decrease... Mountain Hikes (talk) 04:01, 17 December 2015 (UTC)
Why is he breaking from his usual black and white style? The green was a suprise 162.158.39.207 22:06, 27 November 2016 (UTC)Davy
England is part of the mainland of Britain and can't float anywhere on its own without tearing itself away from the rest of the land. It's like suggesting that California can float away from America. (Maybe that wasn't a good example, what with the San Andreas Fault, and all...) Brenda (talk) 09:52, 15 June 2018 (UTC)
The final number does not agree with the inputs provided in the example. I get 3.00, not 3.51, when I follow the data on the page. Additionally, when I put I use the range or core pressures provided, I get between 2.92 and 3.18. That confirms the comic's assertion with the provided data.--172.69.33.211 18:14, 28 September 2022 (UTC)
Toyota *has* made a better Prius. As of the 2025 model year achieving 57 mpg, England must have drifted out to sea by ~4.5km, making the English Channel ~37.7km wide. 108.162.245.126 20:47, 15 May 2025 (UTC)